《IDENTITY-BASED CRYPTOSYSTEMS AND SIGNATURE SCHEMES 》-1984_Adi Shamir(中文翻译)
基于身份的密码系统和签名方案
Adi Shamir
想法
在本文中,我们介绍了一种新型的密码方案,它使任何一对用户都可以安全地通信并验证彼此的签名,而不需要交换私有或公共密钥,不需要保留密钥目录,也不需要使用第三方的服务。该方案假设存在可信密钥生成中心,其唯一目的是在用户首次入网时为其提供个性化智能卡。此卡内嵌的信息使用户能够对其发送的消息进行签名和加密,并以完全独立的方式对其接收的消息进行解密和验证,而不考虑另一方的身份。以前发行的卡片在新用户加入网络时不需要更新,各个中心不需要协调他们的活动,甚至不需要保存用户列表。这些中心可以在所有的卡片发出后关闭,网络可以在不确定的时间内继续以完全分散的方式运行。
该方案非常适合封闭的用户群体,如跨国公司的高管或大型银行的分支机构,因为公司的总部可以作为一个密钥生成中心,每个人都信任。方案在全国性的成百上千的密钥生成中心和数以百万计的用户中仍然实用,它可以是一种新型的个人的基础电子身份证,每个人都可以签支票,信用卡,法律文件和电子邮件。
该方案基于一个具有外加捻度的公钥密码系统:用户选择自己的名字和网络地址作为公钥,而不是生成一对随机的公/私钥并发布其中的一个密钥。姓名、社会保险号码、街道地址、办公室号码或电话号码的任何组合都可以使用(取决于上下文),只要它能以一种用户后来无法否认的方式唯一地标识用户,而且另一方随时可以使用它。对应的密钥由密钥生成中心计算,并在用户首次入网时以智能卡的形式发给用户。该卡包含一个微处理器、一个I/O端口、一个RAM、一个带有密钥的ROM和用于消息加密/解密的程序。
基于身份的方案类似于理想的邮件系统:如果您知道某人的姓名和地址,就可以向他发送只有他能阅读的消息,并且可以验证只有他才能生成的签名。它使得通信的加密方面对用户来说几乎是透明的,即使是对密钥或协议一无所知的门外汉也可以有效地使用它。
当用户A想要发送消息给用户B时,A用自己的智能卡密钥进行签名,通过使用B的名字和网络地址进行加密,添加A自己的名字和网络地址信息,并将其发送给B。B接收消息时,B使用智能卡密钥解密消息,然后通过使用发送者的名字和地址作为一个验证密钥进行验证签名。
密钥必须由密钥生成中心而非用户计算,因为用户的身份没有什么特别之处:如果用户可以计算密钥对应的公钥“A”,他也可以计算密钥对应的公钥“B”,“C”等,那么这个方案将是不安全的。密钥生成中心可以通过知道一些秘密信息(如一个大数字的因数分解)来获得特权,从而能够计算出网络中所有用户的密钥。
该方案的整体安全性取决于以下几点:
- 底层密码函数的安全性。
- 特权信息安全的储存在密钥生成中心。
- 密钥生成中心在分发他们的卡片给用户前,进行身份的彻底性检查。
- 防止用户卡片的遗失、复制或未经授权的使用而采取的预防措施。
密码方案有效地将消息与身份信息 i i i 绑定在一起,而卡的所有权有效地将身份信息 i i i 与物理用户绑定在一起。与其他发行身份证的机构一样,该中心必须仔细筛选申请卡片的人,以防止虚假陈述,并必须仔细保护其“印章”,以防伪造。用户可以通过密码系统或记忆部分密钥来保护自己免受未经授权的使用。
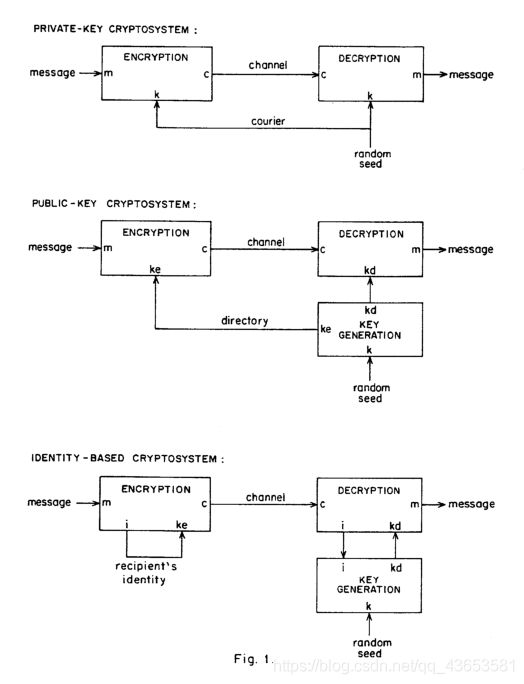
图一总结了公钥、私钥和基于身份的密码体系的区别(见最末尾)。在这些方案中,消息 m m m 通过密钥 k e ke ke 进行加密,在公共的信道以密文 c c c 的形式传输,通过密钥 k d kd kd 解密。密钥的选择是基于一个随机种子 k k k 的。在私钥方案中, k e = k d = k ke = kd = k ke=kd=k ,单独的密钥通道(通常是一个信使)必须同时保持密钥的保密性和真实性。在公钥方案中,加密和解密密钥由 k k k 通过两个不同的函数 k e = f e ( k ) ke=fe(k) ke=fe(k) 和 k d = f d ( k ) kd = fd(k) kd=fd(k) 生成,而单独的密钥通道(通常是一个目录)必须只保留密钥的真实性。在基于身份的方案中,加密密钥是用户的身份标识 k e = i ke = i ke=i,解密密钥由 i i i 和 k k k 通过 k d = f ( i , k ) kd = f(i,k) kd=f(i,k)生成。用户之间单独的密钥通道被完全消除,当接收者首次加入网络时,(密钥通道)被与密钥生成中心的单一交互所取代。
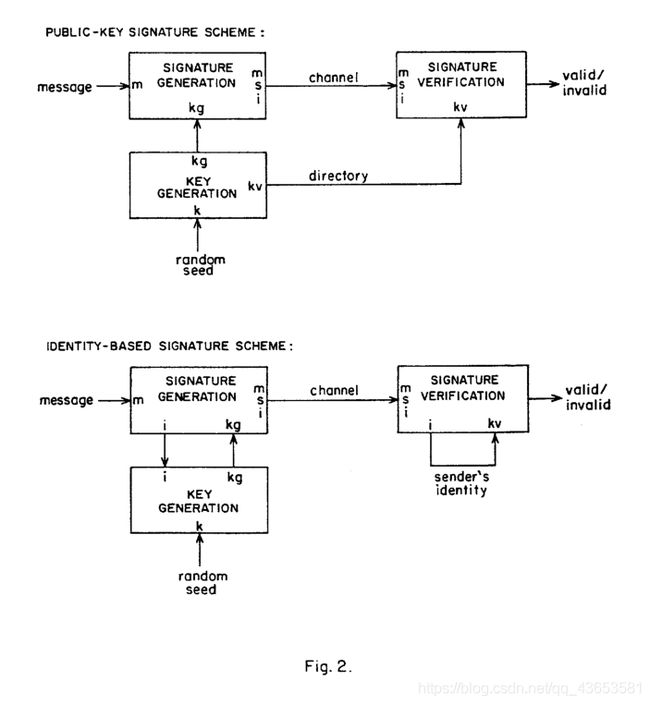
公钥和基于身份的签名方案是对应密码系统的镜像,如图2所示(见最末尾)。消息m 使用生成的签名密钥 k g kg kg 进行签名,签名后的 s s s 与发送者的身份标识 i i i 一起传输,使用签名验证密码 k v kv kv 能够对其进行验证。图表的其余部分应该是不言而喻的。
实现
为了实现上一节所描述的思想,我们需要一个带有两个附加属性的公钥方案:(a)当随机数 k k k 被已知时,可以很容易的计算出可能的公钥中不可忽略的一部分(即密钥)。(b)用这个 k k k生成的特定公/私钥对来计算随机数 k k k是一个棘手的问题。
不幸的是,RSA方案不能被使用,因为它不能同时满足这些条件:(a)如果模 n n n 是用户身份的伪随机函数,即使是密码生成中心也不能因式分解,不能从加密质数 e e e 计算解密质数 d d d 。(b)如果模n是更一般的,种子是它的秘密因式分解,那么任何知道加密质数 e e e 及其对应的解密指数 d d d 的人都可以计算随机种子。
在这个阶段,我们构建了具体的实施方案,仅仅基于身份的签名方案,但我们推测,基于身份的密码系统也存在,我们鼓励读者寻找这种的系统。这种情况让人想起1976年的情况,当时定义了公钥密码系统,并研究了它们的潜在应用,尽管第一个具体实现直到1978年才发布。
签名方案是基于验证条件:
s e = i ⋅ t f ( t , m ) ( m o d n ) s^e=i \cdot t^{f(t,m)} \ (mod \ n) se=i⋅tf(t,m) (mod n)
这里:
- m m m 是消息
- s , t s, t s,t 是签名
- i i i 是用户的身份标识
- n n n 是两个大素数的乘积
- e e e 是一个相对于 φ ( n ) \varphi (n) φ(n) 的一个大素数
- f f f 是一个单向函数
参数 n 、 e n、e n、e 和函数 f f f 由密码生成中心选择,所有用户的智能卡中都存储有相同的 n 、 e n、e n、e 和相同的 f f f 算法描述。这些值可以公开,但是 n n n 的因式分解只能由密钥生成中心知道。用户之间唯一的不同是 i i i 的值,与 i i i 相对应的密钥是(唯一的)数字 g g g ,使得
g e = i ( m o d n ) g^e = i \ (mod \ n) ge=i (mod n)
这个 g g g 可以很容易由密钥生成中心计算出来,但是如果RSA方案是安全的,没有人能够提取 e e e次根模 n n n (即对于 n n n 的指数型分解)。
每个消息 m m m 都有大量可能的(s,t)签名,但是它们的密度很低,随机搜索极不可能发现任何一个。任何将(s,t)中的一个设为随机值并求另外一个变量的尝试都需要提取模的根号,这被认为是一项极其困难的计算任务。然而,当 g g g 已知时,有一种非常简单的办法可以生成任意数量的任何消息签名,即使 n n n 的因式分解是未知的。
为了对消息 m m m 进行签名,用户选择一个随机数 r r r 并计算
t = r e ( m o d n ) t = r^e \ (mod \ n) t=re (mod n)
验证条件可以重写为
s e = g e ⋅ r e f ( t , m ) ( m o d n ) s^e = g^e \cdot r^{ef(t,m)} \ (mod \ n) se=ge⋅ref(t,m) (mod n)
由于 e e e 相对于 φ ( n ) \varphi (n) φ(n) 的素数,我们可以从指数中消去公因数
s = g ⋅ r f ( t , m ) ( m o d n ) s = g \cdot r^{f(t,m)} \ (mod \ n) s=g⋅rf(t,m) (mod n)
因此,无需任何根的提取即可计算 s s s 。
为了防止基于不同用户的身份(以及 g g g 值)之前乘法关系的攻击,建议通过一个通用单向函数将描述用户身份的字符串扩展为一个长伪随机字符串,并在验证条件下使用扩展形式 i i i 。由于网络中的每个人都知道如何应用这个功能,所以该方案保留了它的基于身份的风格,即使签名验证密钥严格来说并不等于用户的身份。
该方案的安全性取决于密码分析人员无法通过分析他所选择的大量有效的消息签名来隔离 g g g 。如果 f f f 和 e e e 的最大公约数 c ≠ 1 c \neq 1 c=1 ,通过操作验证条件是可能得到 c c c 次根,因此,有必要使 e e e 成为一个足够大的素数,是 f f f 称为一个足够强的单向函数,这样,这种情况就不会在实践中出现。 r r r 的值不应该被重复使用或透露,因为 g g g 在任何具体的签名中都受到它的随机性和保密性的保护。
消除 t t t 的两个出现之一(例如,用常量替换它)的验证条件的变体是不安全的。因此,使用一个将 t t t 和 m m m 完全混合的单向函数是很重要的(最好是通过非算术和非可逆性操作),并且该函数有很大的可能值范围。
我们认为,适当选择参数可以使该方案变得非常安全,但我们不能证明破解它等于解决一些众所周知的计算问题。它的主要目的是启发,作为第一个证明存在基于身份的方案。Ong-Schnorr-Shamir 签名方案也可以作为一个基于身份的方案使用,但它的安全性仍然是一个开放的问题,因为Pollard成功地攻破了它的早期版本。一如既往地,我们不建议在密码社区有足够的时间评估其安全性之前立即使用此方案。
致谢
我要感谢Amos Fiat、Heidroon Ong和Claus Schnorr的非常有益的讨论。