2019/7/16更新:封装SplayTree进入class:例题:http://poj.org/problem?id=3622
一个伸展树的板子:
#include
#include
#include
#include
#include
// srand(unsigned)time(NULL));rand();
#include
在开头写下伸展树的应用情况,以及使用方法,由于本人是个蒟蒻,因此总结不为全面,有更多的方法希望指出和提醒:
对于伸展树的一些应用:
因为伸展树和核心是 旋转节点 ,所以我们就从旋转节点处开始入手,进行一些 骚操作。
1.裸的伸展树,实现增删改查,对节点的直接操作,比较简单,会板子就行
2.对区间的修改,例:对区间[a,b]修改,
可以将节点a-1旋转到根节点的位置,将b+1旋转到根节点的右子节点,
这样的话,根节点的右子节点的左子树就是区间[a,b];
我们可以直接对于每个节点里面储存的信息进行修改
(节点中可以储存以该节点为根节点的一些信息,修改也好修改,旋转向下传递)
3.在a后面插入一些数,那么我们先把插入的这些数建成一颗伸展树,
用分治法建立一颗完全平衡的二叉树,
就是说每次把最中间的节点转到根节点的右边,
最后将这颗新的子树挂到 根右子节点的左子节点上
4.删除一个区间[a,b]内的数 ,可以参考第二种情况,
旋转,然后直接删除一个一颗子树,继续维护伸展树
5.区间的翻转,对区间[a,b]的翻转,可以引用一个lazy数组进行标记,每次旋转的时候判断一下,翻转则翻转左右子节点,然后向下推一个节点,然后刷新本节点lazy数组。
/*-----------------------伸展树----------------------------*/
伸展数(Splay Tree),又叫分裂树,是一种二叉排序树,能在O(log n)内完成插入,查找,删除操作;
伸展树上的一般操作都基于伸展操作:
假设要对一个二叉查找树执行一系列查找操作,为使整个查找时间更小,被查效率高的那些条目应当经常处于靠近树根的位置;
于是想设计一个简单方法,在每次查找之后对树进行重构,把被查找的条目搬移到离树根近一些的地方。
伸展树是一种自调形式的二叉查找树,他会沿着从某个节点到树根之间的路径,通过一系列旋转的把这个节点搬移到树根去。
它的优势在于不需要记录用于平衡树的冗余信息。
关键词:
二叉排序树 平衡树
因此我决定先学这两个数据结构:
//--------------------二叉排序树:
又称 二叉查找树||二叉搜索树
定义:
二叉排序树或者一颗空树,或者具有下列性质的二叉树:
1.若左子树不空,则左子树上所有节点的值均小于它的根节点的值;
2.若右子树不空则右子树上所有节点的值均大于它的根节点的值;
3.左右子树分别为二叉排序树;
4.没有 键值 相等的节点
//键值(key):
//键值是 window 中注册表中的概念。键值位于注册表结构链末端,和文件系统的文件类似;
//键值包含集中数据类型,以适应不同环境的使用需求。
// 注册表中,是通过键和子键来管理各种信息;
简单的说 二叉排序树就是一棵从左往右越来越大的树。
//---查找:
若根节点的关键字等于查找的关键字,成功
否则,判断查找关键字值,递归进入左子树或右子树
子树为空,查找不成功
//---插入删除:
二叉排序树是一种动态树表,其特点是:树的结构通常不是一次生成的,而是在查找过程中,当树中不存在关键字等于给定值时在进行插入。
新插入的节点一定是一个新添加的叶子节点而且查找不成功时查找路径上访问的最后一个节点的左||右子节点
插入算法:
首先执行查找算法,找出被插节点的父节点;
判断被插节点是其父节点的左||右子节点,被插节点作为子节点插入。
若二叉树为空,则首先单独生成根节点。
新插入的节点总是叶子节点。
struct bitree{
int data;
bitree *lchild,*rchild;
};
//在二叉排序树中插入查找关键字key
bitree* insertbst(bitree *t,int key)
{
if(t==NULL)
{
t=new bitree();
t->lchild=t->rchild=NULL;
t->data=key;
return t;
}
if(keydata)
t->lchild=insertbst(t->lchild,key);
else
t->rchild=insertbst(t->rchild,key);
return t;
}
//n个数据在数组d中,tree为二叉排序树 树根
bitree* create_bitree(bitree *tree,int d[],int n)
{
for(int i=0;idata.key)//找到关键字等于key的数据元素
return Delete(parent_t,t);
else if(keylchild.key)
return Deletebst(T,T->lchild,key);
else
return Deletebst(T,T->rchild,key);
}
return true;
}
bool Delete(bitree &fp,bitree &p)
{//从二叉排序树中删除节点p,并重接它的左||右子树
if(!p->rchild)//只需要连接一棵树即可
{
fp->lchild=p->lchild;
delete(p);
}
else if(!p->lchild)
{
fp->rchild=p->rchild;
delete(p);
}
else//连接两棵树
{
q=p;
fp->lchild=p->lchild;
s=p->lchild;//转左
while(s->rchild)//向右到尽头
{
q=s;
s=s->rchild;
}//此时q是s的父节点
s->rchild=p->rchild;//将s的左子树作为q的右子树
delete(p);
}
return true;
}
//----------------平衡树
平衡二叉树(Balanced Binary Tree)具有以下性质:
它是一颗空树||它的左右两个子树高度差的绝对值不超过1,并且左右两个子树都是一颗平衡二叉树。
平衡树的实现方法有:
红黑树,AVL,替罪羊树,Treap,伸展树等
最小平衡二叉树节点的公式:F(n)=F(n-1)/*左子树树节点数量*/+F(n-2)/*右子树节点数量*/+1;
平衡树的维持方法:
二叉左旋:
//待学习。。。
二叉右旋:
//待学习。。。
//---------------------------了解完基础知识,开始学习伸展树--------
如何构造一个伸展树:
//---方法一:
访问到X节点时,从X处单旋转将X移动到根节点处,
也就是将访问路径上的每个节点和他们的父节点都实施旋转 。
这种旋转的效果是将访问节点X一直推向树根,
但是不好的地方是可能将其他节点推向更深的位置,
这种效果并不好,因为它没有改变访问路径上其他节点的后序访问状况。
//---方法二:
和方法一类似,
在访问到节点X时,根据X节点和其父节点(P)以及祖父节点(G)之间的形状做相应的单选转或双旋转。
如果三个节点构成LR或RL时(即之字型),则进行相应的双旋转;
如果构成LL或者RR时进行对应的单选转(一字型)。
这样展开的效果是将X推向根节点的同时,
访问路径上其他节点的深度大致都减少了一半
(某些浅的节点最多向后退后了两层)。
这样做对绝大多数访问路径上的节点的后续访问都是有益的。
//-----伸展树的基本特性:
当访问路径太长而导致超出正常查找时间的时候,这些旋转将对未来的操作(下一次访问)有益;
当访问耗时很少的时候,这些旋转则不那么有益甚至有害。
/*--一个(舍弃)的 解释
//------伸展树的基本操作
伸展树的伸展方式有两种,一种是自下向上的伸展;另一种是自上向下的伸展。
比较容易理解的是自下向上的伸展,我们会重点解释自顶向下的实现方式。
//---自下向上
先自上向下搜寻X节点,
当搜索到X节点时,从X节点开始到根节点的路径上所有的节点进行旋转 ,
最终将X节点推向根节点,将访问路径上的大部分节点的深度都降低。
具体旋转需根据不同的情形进行,在X节点处有三种情形需要考虑
(假设X的父节点是P,X的祖父节点为G):
1.X的父节点P就是树根的情形,这种情形比较简单,只需要将X和P进行旋转即可,
X和P构成LL就是左单选转,构成RR就右单旋转
2.X和P和G之间构成"之"字型的情形,即LR||RL类型。
如果是LR则进行左双旋转,如果是RL进行右双旋转 。
3.X和P和G之间构成"一"字形的情形,即RR||LL类型;
如果LL则执行两次单左旋转,如果是RR则执行两次单右旋转;
代码先不写了:效率据说不高
//--自顶向下的伸展
*/
自顶向下的伸展:
换成图片就是这样:
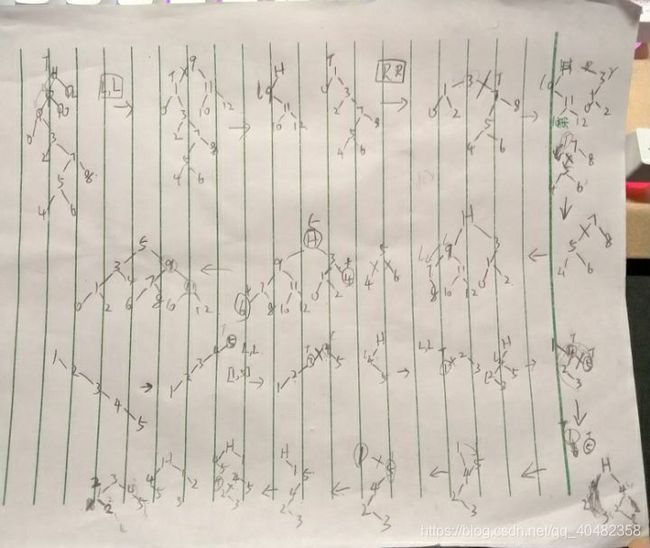
然后是运行的代码:
#include
#include
#include
using namespace std;
struct splaytree_node{
int key;
splaytree_node *left,*right;
};
splaytree_node *splaytree_search(splaytree_node *x,int key)//递归查找
{
if(x==NULL||x->key==key)
return x;
if(keykey)
return splaytree_search(x->left,key);
else
return splaytree_search(x->right,key);
}
splaytree_node *splaytree_splay(splaytree_node *tree,int key)//旋转
{
splaytree_node N,*l,*r,*c;
if(tree==NULL)
return tree;
N.left=N.right=NULL;
l=r=&N;
while(1)//开始旋转调整
{
//cout<key<key)//向l方向调整
{
if(tree->left==NULL)//左边没东西了
break;
if(keyleft->key)//左边仍有值 && key仍小于
{
c=tree->left;
tree->left=c->right;
c->right=tree;
tree=c;
//现在已经调整过节点 向左旋转一个节点
if(tree->left==NULL)
break;//如果左边没有值了,就结束循环
}
r->left=tree;
r=tree;
tree=tree->left;
}
else if(key>tree->key)//向r方向调整
{
if(tree->right==NULL)
break;
if(key>tree->right->key)
{
c=tree->right;
tree->right=c->left;
c->left=tree;
tree=c;
if(tree->right=NULL)
break;
}
l->right=tree;
l=tree;
tree=tree->right;
}
else// 已经是该节点了
{
break;
}
}
//当亲位置 tree为目标点||最接近目标点
// cout<key<<" "<left<<" "<right<right=tree->left;
r->left=tree->right;
tree->left=N.right;
tree->right=N.left;
// cout<key<<" "<left<<" "<right<key=key;
p->left=left;
p->right=right;
return p;
}
splaytree_node *insert_node(splaytree_node* tree,splaytree_node *z)
{
splaytree_node *y=NULL;//要插入的目标位置的上一个位置
splaytree_node *x=tree;//要插入的目标位置
while(x!=NULL)
{
y=x;
if(z->keykey)
x=x->left;
else if(z->key>x->key)
x=x->right;
else
{
cout<<"Error:此节点已存在!"<keykey)//y的左节点
y->left=z;
else
y->right=z;//y的右节点
return tree;
}
splaytree_node *splaytree_insert(splaytree_node *tree,int key)//插入
{
//cout<key<<" "<key<<" "<left!=NULL)
{
x=splaytree_splay(tree->left,key);
//将根节点左子树最大的节点旋转为根节点
x->right=tree->right;
}
else
x=tree->right;
free(tree);
return x;
}
void print_splaytree(splaytree_node *tree,int key,int direction)//打印树
{
if(tree!=NULL)
{
if(direction==0)
cout<key<<" is root"<key<<" is "<left,tree->key,-1);
print_splaytree(tree->right,tree->key,1);
}
}
/*
10
1 2 3 4 5 6 7 8 9 10
7
*/
int main()
{
//插入
int n;
cin>>n;
splaytree_node *root=NULL;
int data;
for(int i=1;i<=n;++i)
{
cin>>data;
root=splaytree_insert(root,data);
//cout<key,0);
}
cout<<"delete a node"<>data;
root=splaytree_delete(root,data);
print_splaytree(root,root->key,0);
}
由于自顶向下伸展会导致,节点刷新的时候需要重新刷新,因此,在比较自下至上伸展之后,发现自下向上伸展对节点的维护更加方便,因此,下面学习伸展树的自下向上的伸展:
其实自下而上的伸展和自上而下的类似,直接上板子了:
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
//#include
下面是一个用数组模拟的板子,以后就不用每次都delete了:
就以HDU-3487为例子写的一个板子:
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
#include
//#include
然后是我用子节的那个板子修改的结构体版,最后是格式错误,但是答案是对的,而且时间也差不多:
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
//#include
然后是区间的增加和修改:
以POJ-3468为例(其实这道题用线段树更好,伸展树的话,时间用的会更加长)
ac:4800ms+
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
//#include
