极大似然估计学习笔记
概念
1 概率和统计:概率是已知模型和参数,推数据。统计是已知数据,推模型和参数;
2 极大似然估计(Maximum likelihood estimation,简称MLE):俗理解来说,就是利用已知的样本结果信息,反推最具有可能(最大概率)导致这些样本结果出现的模型参数值,换句话说,极大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”;
3 极大似然估计的前提假设:所有的采样都是独立同分布的。
似然函数始末
在散型的情形下,随机变量 X X X的概率分布是已知的,但是该分布的参数 θ \theta θ未知,需要我们通过一定方法估计。举一个例子:
现有三个不标准的硬币,其中第一枚抛出后正面朝上的概率为 2 5 \frac{2}{5} 52,第二枚硬币抛出后正面朝上的概率为 1 2 \frac{1}{2} 21,第三枚抛出后正面朝上的概率为 3 5 \frac{3}{5} 53。取出其中一枚硬币,抛掷20次,其中正面朝上的次数为13次,请问取出的是第几枚硬币。
答: 分别计算三枚硬币抛掷20次,有13次正面朝上的概率:
第一枚:
C 20 13 ( 2 5 ) 13 ( 1 − 2 5 ) 20 − 13 = 0.01456305 C_{20}^{13}(\frac{2}{5})^{13}(1-\frac{2}{5})^{20-13}=0.01456305 C2013(52)13(1−52)20−13=0.01456305
第二枚:
C 20 13 ( 1 2 ) 13 ( 1 − 1 2 ) 20 − 13 = 0.07392883 C_{20}^{13}(\frac{1}{2})^{13}(1-\frac{1}{2})^{20-13} = 0.07392883 C2013(21)13(1−21)20−13=0.07392883
第三枚:
C 20 13 ( 3 5 ) 13 ( 1 − 3 5 ) 20 − 13 = 0.165882265 C_{20}^{13}(\frac{3}{5})^{13}(1-\frac{3}{5})^{20-13} = 0.165882265 C2013(53)13(1−53)20−13=0.165882265
所以这枚硬币更可能是第三枚。
我们的参数 θ \theta θ就是上例中待估计的正面向上的概率值。对应到上例,随机变量 X X X的取值 x i x_i xi表示抛掷 k k k次硬币,正面向上的次数,这个概率为:
P ( { X = x i } ) = C k x i θ x i ( 1 − θ ) k − x i P(\{X=x_i\})=C_{k}^{x_i}\theta^{x_i}(1-\theta)^{k-x_i} P({X=xi})=Ckxiθxi(1−θ)k−xi
其中, x i x_i xi、 k k k这些参数是已知的,参数 θ \theta θ是未知的,因此抛掷 k k k次硬币,有 x i x_i xi次向上的概率是一个关于参数 θ \theta θ的函数,写作:
P ( { X = x i } ) = p ( x i ; θ ) P(\{X=x_i\})=p(x_i;\theta) P({X=xi})=p(xi;θ)
如果做 n n n次这样的实验,每一次实验中,都是连续抛掷 k k k次硬币,统计出现正面的次数,得到一系列样本: x 1 , x 2 , x 3 , . . . , x n x_1, x_2, x_3, ..., x_n x1,x2,x3,...,xn,这些样本的取值之间满足相互独立,那么这一串样本取得上述取值 { X 1 = x 1 , X 2 = x 2 , X 3 = x 3 , . . . , X n = x n } \{X_1=x_1,X_2=x_2,X_3=x_3,...,X_n=x_n\} {X1=x1,X2=x2,X3=x3,...,Xn=xn}的联合概率为:
∏ i = 1 n p ( x i ; θ ) = p ( x 1 ; θ ) ⋅ p ( x 2 ; θ ) ⋅ p ( x 3 ; θ ) ⋅ . . . ⋅ p ( x n ; θ ) \prod_{i=1}^np(x_i;\theta)=p(x_1;\theta)\centerdot p(x_2;\theta)\centerdot p(x_3;\theta)\centerdot...\centerdot p(x_n;\theta) i=1∏np(xi;θ)=p(x1;θ)⋅p(x2;θ)⋅p(x3;θ)⋅...⋅p(xn;θ)
变换一下形式:
L ( θ ) = L ( x 1 , x 2 , x 3 , . . . , x n ; θ ) = ∏ i = 1 n p ( x i ; θ ) L(\theta)=L(x_1, x_2, x_3, ..., x_n;\theta)=\prod_{i=1}^np(x_i;\theta) L(θ)=L(x1,x2,x3,...,xn;θ)=i=1∏np(xi;θ)
L ( θ ) L(\theta) L(θ)就是已知样本值 x 1 , x 2 , x 3 , . . . , x n x_1, x_2, x_3, ..., x_n x1,x2,x3,...,xn的似然函数,它描述的是取得这一串指定样本值的概率值,而这个概率值完全由未知参数 θ \theta θ决定。
如果 X X X是一个连续型随机变量,则:
L ( θ ) = L ( x 1 , x 2 , x 3 , . . . , x n ; θ ) = ∏ i = 1 n f ( x i ; θ ) L(\theta)=L(x_1, x_2, x_3, ..., x_n;\theta)=\prod_{i=1}^nf(x_i;\theta) L(θ)=L(x1,x2,x3,...,xn;θ)=i=1∏nf(xi;θ)
极大似然估计原理
思想
显然,似然函数 L ( θ ) = L ( x 1 , x 2 , x 3 , . . . , x n ; θ ) L(\theta)=L(x_1, x_2, x_3, ..., x_n;\theta) L(θ)=L(x1,x2,x3,...,xn;θ)是指随机变量 X X X取到指定的一组样本值 x 1 , x 2 , x 3 , . . . , x n x_1, x_2, x_3, ..., x_n x1,x2,x3,...,xn时的概率大小。当未知的待估计参数 θ \theta θ取不同的值时,计算出来的该列车的值会发生变化。
例如,当 θ = θ 0 \theta=\theta_0 θ=θ0时,似然函数 L ( x 1 , x 2 , x 3 , . . . , x n ; θ 0 ) L(x_1, x_2, x_3, ..., x_n;\theta_0) L(x1,x2,x3,...,xn;θ0)的取值为0或趋近于0,那么意味着当 θ = θ 0 \theta=\theta_0 θ=θ0时,随机变量 X X X取得这一组样本 x 1 , x 2 , x 3 , . . . , x n x_1, x_2, x_3, ..., x_n x1,x2,x3,...,xn的概率为0,即根本不可能或可能性极小得到这样一组样本值,那么就不应该取 θ 0 \theta_0 θ0为参数估计值。
如果当 θ \theta θ取 θ 1 \theta_1 θ1和 θ 2 \theta_2 θ2两种不同的值时,似然函数的值 L ( x 1 , x 2 , x 3 , . . . , x n ; θ 1 ) > L ( x 1 , x 2 , x 3 , . . . , x n ; θ 2 ) L(x_1, x_2, x_3, ..., x_n;\theta_1) \gt L(x_1, x_2, x_3, ..., x_n;\theta_2) L(x1,x2,x3,...,xn;θ1)>L(x1,x2,x3,...,xn;θ2),即 θ \theta θ取 θ 1 \theta_1 θ1比取 θ 2 \theta_2 θ2有更大的可能获得这一组样本值 x 1 , x 2 , x 3 , . . . , x n x_1, x_2, x_3, ..., x_n x1,x2,x3,...,xn,所以在选取估计值时更倾向于选取 θ 1 \theta_1 θ1。
因此我们需要做的就是在未知参数 θ \theta θ的取值范围 Θ \Theta Θ中选取使得似然函数 L ( x 1 , x 2 , x 3 , . . . , x n ; θ ) L(x_1, x_2, x_3, ..., x_n;\theta) L(x1,x2,x3,...,xn;θ)能够取得最大值的 θ ^ \hat{\theta} θ^,作为未知参数的估计值,由于 θ ^ \hat{\theta} θ^使得似然函数取值达到最大,因此 θ ^ \hat{\theta} θ^就是未知参数 θ \theta θ的极大似然估计。
计算
在给定概率模型和一组相互独立的观测样本 x 1 , x 2 , x 3 , . . . , x n x_1, x_2, x_3, ..., x_n x1,x2,x3,...,xn的基础之上,求使得似然函数 L ( θ ) = L ( x 1 , x 2 , x 3 , . . . , x n ; θ ) = ∏ i = 1 n p ( x i ; θ ) L(\theta)=L(x_1, x_2, x_3, ..., x_n;\theta)=\prod_{i=1}^np(x_i;\theta) L(θ)=L(x1,x2,x3,...,xn;θ)=∏i=1np(xi;θ)取得最大值的未知参数 θ \theta θ的取值(连续情况类似)。
那么,就直接对似然函数求导,使得导数为0的 θ \theta θ的取值,就是我们要找的极大似然估计值 θ ^ \hat{\theta} θ^。由于函数 g ( x ) g(x) g(x)和函数 l n ( g ( x ) ) ln(g(x)) ln(g(x))的单调性时一致的,并且 L ( θ ) L(\theta) L(θ)的式子都是连乘,所以将其转换成 l n ( L ( θ ) ) ln(L(\theta)) ln(L(θ)):
l n ( L ( θ ) ) = l n ( ∏ i = 1 n p ( x i ; θ ) ) = ∑ i = 1 n l n ( p ( x i ; θ ) ) ln(L(\theta))=ln(\prod_{i=1}^np(x_i;\theta))=\sum_{i=1}^nln(p(x_i;\theta)) ln(L(θ))=ln(i=1∏np(xi;θ))=i=1∑nln(p(xi;θ))
此时在对该函数求导,如果上式有唯一解,并且还是最大值点,那么那就是我们要求的极大似然估计值。
更一般的,对于多参数情况:
l n ( L ( θ 1 , θ 2 , . . . , θ k ) ) = l n ( ∏ i = 1 n p ( x i ; θ 1 , θ 2 , . . . , θ k ) ) = ∑ i = 1 n l n ( p ( x i ; θ 1 , θ 2 , . . . , θ k ) ) ln(L(\theta_1,\theta_2,...,\theta_k))=ln(\prod_{i=1}^np(x_i;\theta_1,\theta_2,...,\theta_k))=\sum_{i=1}^nln(p(x_i;\theta_1,\theta_2,...,\theta_k)) ln(L(θ1,θ2,...,θk))=ln(i=1∏np(xi;θ1,θ2,...,θk))=i=1∑nln(p(xi;θ1,θ2,...,θk))
然后对于每一个待估计的未知参数 θ i \theta_i θi,都求偏导数,并令其为零,得到如下方程式:
{ ∂ l n L ∂ θ 1 = 0 ∂ l n L ∂ θ 2 = 0 ⋅ ⋅ ⋅ ∂ l n L ∂ θ k = 0 \begin{cases} \frac{\partial lnL}{\partial \theta_1}=0 \\ \frac{\partial lnL}{\partial \theta_2}=0 \\ \ \centerdot \centerdot \centerdot \\ \frac{\partial lnL}{\partial \theta_k}=0 \end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧∂θ1∂lnL=0∂θ2∂lnL=0 ⋅⋅⋅∂θk∂lnL=0
解出该方程即可。
需要注意的是极大似然估计值可能不存在,并且如果存在也有可能它的值不唯一。可以参考下面两个图:
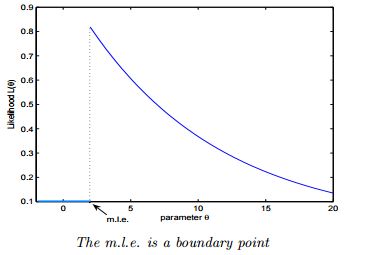
如果极大似然函数 L ( θ ) L(\theta) L(θ)在极大值处不连续,一阶导数不存在,则 MLE 不存在。

MLE不唯一的情况。