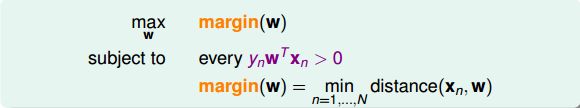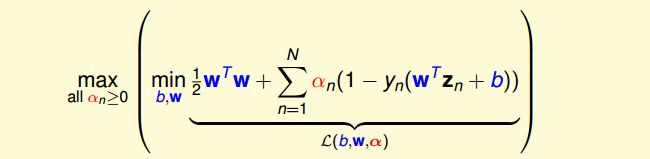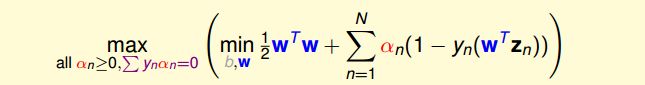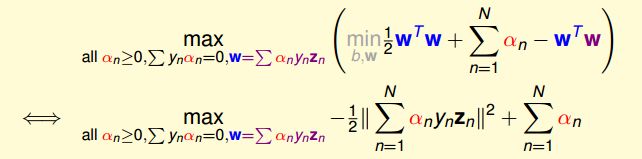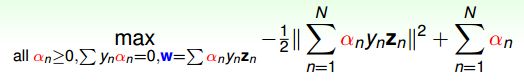机器学习笔记--常见算法(9)--support vector machine(SVM)（台大林轩田SVM）

1. Liner Support Vector Machine

1.1 SVM引出

SVM是一种分类器。现在有两种类别(如下图)，我们要找到一条直线，将两个不同的类别区分开。图中存在许多满足条件的直线，我们该选哪条最合适呢？

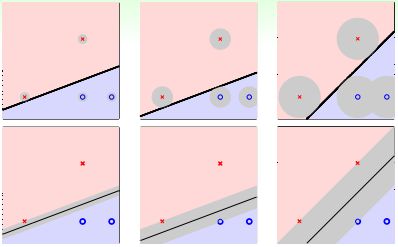
直观上来说，我们有几种考虑因素：①能容忍更多噪声，②模型更健壮，不会过拟合。
这个问题可以等价于：选择一条直线，判断该直线到最近的点的距离究竟是远还是近。我们希望这条直线更"fat"(如上图最后一条直线)，也就是直线到最近的点的距离越远越好。

1.2 SVM中的margin计算

定义分类线有多胖，也就是看距离分类线最近的点与分类线的距离，我们把它用margin表示。
整体来说，我们的目标就是找到这样的分类线并满足下列条件：

• 分类正确。能把所有正负类分开。即$y_n{\omega }^T{x}_n>0$
• margin最大化
  

有了上述条件，那么如何计算点到分类线的距离呢？

为了便于计算，做一个小小的改动，将$\omega ({\omega }_0,{\omega }_1,\dots ,{\omega }_d)$中的${\omega }_0$拿出，替换为b。同时省去$x_0$项。假设函数hypothesis就变成了$h(x)=sign({\omega }^{T}x+b)$。

那么，点到分类平面的距离公式为：（推导见视频）
$distance(x,b,w)=|\frac{{\omega }^T}{||\omega ||}(x-x^{\prime })|=\frac{1}{||\omega ||}|{\omega }^{T}x+b|$

具体的求距离步骤：
①写出hyperplane ${\omega }_{1}x1+{\omega }_{2}x2+...+{\omega }_{d}xd+b=0$的形式
②求$||\omega ||=\sqrt{{\omega }_1^2+{\omega }_2^2+...+{\omega }_d^2}$
③将距hyperplane最近的点代入${\omega }^{T}x=b$中
④求③绝对值，代入距离公式计算最终结果

1.3 margin计算公式的简化

为了简化计算，做一个放缩，令距离分类面最近的点满足$y_n(w^T{x}_n+b)=1$。那么我们所要求的margin就变成了：
$margin(b,w)=\frac{1}{||w||}$

目标形式简化为：

另外，最大化问题$max\frac{1}{||w||}$可转换为最小化问题$min\frac{1}{2}{\omega }^T\omega$。
放松条件（放松条件对我们毫无影响，见视频1.3 16:00），最终形式为：

1.4 SVM一般求解方法

现在，SVM的标准问题为：

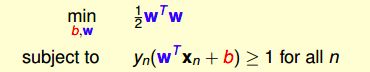
这是一个典型的二次规划问题，即Quadratic Programming(QP)。将SVM与标准二次规划问题的参数一一对应起来，就可以将参数输入一些软件(如matlab)自带的二次规划的库函数求解。

那么，线性SVM算法可以总结为三步：
①计算对应的二次规划参数Q、p、A、c
②根据二次规划库函数，计算$b,\omega$
③将$b,\omega$代入$g_{SVM}$，得到最佳分类面。

1.5 非线性SVM

如果是非线性的，例如包含x的高阶项，那么可以使用在《机器学习基石》课程中介绍的特征转换的方法，先作$z_n=\Phi (x_n)$的特征变换，从非线性的x域映射到线性的z域空间，再利用Linear Hard-Margin SVM Algorithm求解即可。

PS：使用SVM得到large-margin，减少了有效的VC Dimension，限制了模型复杂度；另一方面，使用特征转换，目的是让模型更复杂，减少$E_{i}n$。所以，非线性SVM是把这两者的目的结合起来，平衡这两者的关系。

2.Dual Support Vector Machine

2.1 Dual SVM引出

在1.5节中，对于非线性SVM，可以使用非线性变换将变量从x域转换到z域中，再使用线性SVM解决即可。
然而，特征转换下，设求解QP问题在z域中的维度为为$\hat{d}+1$，如果模型越复杂，则$\hat{d}+1$越大，相应求解这个QP问题也变得很困难。当$\hat{d}$无限大的时候，问题将会变得难以求解，那么有没有什么办法可以解决这个问题呢？一种方法就是使SVM的求解过程不依赖$\hat{d}$，这就是我们本节课所要讨论的主要内容。
把问题转化为对偶问题，同样是二次规划，只不过变量个数编程N个，有N+1个限制条件。这种对偶SVM的好处就是问题只跟N有关，与$\hat{d}$无关，这样就不存在当$\hat{d}$无限大难以求解的情况。

2.2 Lagrange Function 拉格朗日函数

如何把问题转化为对偶问题？
首先，把SVM的条件问题转换为非条件为题。对于SVM问题，使用拉格朗日乘子法，令朗格朗日因子为${\alpha }_n$，构造一个函数：

$$L(b,w,\alpha )=\frac{1}{2}{w}^{T}w+\sum _{n=1}^N{\alpha }_n(1-y_n(w^T{z}_n+b))$$
该函数称为拉格朗日函数。

2.3 把SVM构造成非条件问题

下面，利用拉格朗日函数，把SVM构造成一个非条件问题。

该最小化问题中包含了最大化问题，怎么解释呢？首先我们规定拉格朗日因子${\alpha }_n\ge 0$，根据SVM的限定条件可得：$(1-y_n(w^T{z}_n+b))\le 0$，如果没有达到最优解，即有不满足$(1-y_n(w^T{z}_n+b))\le 0$的情况，因为${\alpha }_n\ge 0$，那么必然有${\sum }_n{\alpha }_n(1-y_n(w^T{z}_n+b))\ge 0$。对于这种大于零的情况，其最大值是无解的。如果对于所有的点，均满足$(1-y_n(w^T{z}_n+b))\le 0$，那么必然有${\sum }_n{\alpha }_n(1-y_n(w^T{z}_n+b))\le 0$，则当${\sum }_n{\alpha }_n(1-y_n(w^T{z}_n+b))=0$时，其有最大值，最大值就是我们SVM的目标：$\frac{1}{2}{w}^{T}w$。因此，这种转化为非条件的SVM构造函数的形式是可行的。

2.4 Lagrange Dual SVM

现在，我们已经将SVM问题转化为与拉格朗日因子${\alpha }_n$有关的最大最小值形式。已知${\alpha }_n\ge 0$，那么对于任何固定的${\alpha }^{\prime }$，且${\alpha }_n^{\prime }\ge 0$，一定有如下不等式成立：

对上述不等式右边取最大值，不等式同样成立：

上述不等式表明，我们对SVM的min和max做了对调，满足这样的关系，这叫做Lagrange dual problem。不等式右边是SVM问题的下界，我们接下来的目的就是求出这个下界。

已知$\ge$是一种弱对偶关系，在二次规划QP问题中，如果满足以下三个条件：

• 函数是凸的（convex primal）

• 函数有解（feasible primal）

• 条件是线性的（linear constraints）

那么，上述不等式关系就变成强对偶关系，$\ge$变成=，即一定存在满足条件的解$(b,w,\alpha )$，使等式左边和右边都成立，SVM的解就转化为右边的形式。

经过推导，SVM对偶问题的解已经转化为无条件形式：

其中，上式括号里面的是对拉格朗日函数$L(b,w,\alpha )$计算最小值。那么根据梯度下降算法思想：最小值位置满足梯度为零。首先，令$L(b,w,\alpha )$对参数b的梯度为零：

$$\frac{\partial L(b,w,\alpha )}{\partial b}=0=-\sum _{n=1}^N{\alpha }_n{y}_n$$

也就是说，最优解一定满足${\sum }_{n=1}^N{\alpha }_n{y}_n=0$。那么，我们把这个条件代入计算max条件中（与${\alpha }_n\ge 0$同为条件），并进行化简：

这样，SVM表达式消去了b，问题化简了一些。然后，再根据最小值思想，令$L(b,w,\alpha )$对参数w的梯度为零：

$$\frac{\partial L(b,w,\alpha }{\partial w}=0=w-\sum _{n=1}^N{\alpha }_n{y}_n{z}_n$$

即得到：

$$w=\sum _{n=1}^N{\alpha }_n{y}_n{z}_n$$

也就是说，最优解一定满足$w={\sum }_{n=1}^N{\alpha }_n{y}_n{z}_n$。那么，同样我们把这个条件代入并进行化简：

这样，SVM表达式消去了w，问题更加简化了。这时候的条件有3个：

• all ${\alpha }_n\ge 0$

• ${\sum }_{n=1}^N{\alpha }_n{y}_n=0$

• $w={\sum }_{n=1}^N{\alpha }_n{y}_n{z}_n$

SVM简化为只有${\alpha }_n$的最佳化问题，即计算满足上述三个条件下，函数$-\frac{1}{2}||{\sum }_{n=1}^N{\alpha }_n{y}_n{z}_n|{|}^2+{\sum }_{n=1}^N{\alpha }_n$最小值时对应的${\alpha }_n$是多少。

总结一下，SVM最佳化形式转化为只与${\alpha }_n$有关：

其中，满足最佳化的条件称之为Karush-Kuhn-Tucker(KKT)：

在下一部分中，我们将利用KKT条件来计算最优化问题中的$\alpha$，进而得到b和w。

2.6 解对偶SVM

上面我们已经得到了dual SVM的简化版了，接下来，我们继续对它进行一些优化。首先，将max问题转化为min问题，再做一些条件整理和推导，得到：

显然，这是一个convex的QP问题，且有N个变量${\alpha }_n$，限制条件有N+1个。则根据上一节课讲的QP解法，找到Q，p，A，c对应的值，用软件工具包进行求解即可。

求解过程很清晰，但是值得注意的是，$q_{n,m}=y_n{y}_m{z}_n^T{z}_m$，大部分值是非零的，称为dense。当N很大的时候，例如N=30000，那么对应的$Q_D$的计算量将会很大，存储空间也很大。所以一般情况下，对dual SVM问题的矩阵$Q_D$，需要使用一些特殊的方法，这部分内容就不再赘述了。

得到${\alpha }_n$之后，再根据之前的KKT条件，就可以计算出w和b了。首先利用条件$w=\sum {\alpha }_n{y}_n{z}_n$得到w，然后利用条件${\alpha }_n(1-y_n(w^T{z}_n+b))=0$，取任一${\alpha }_n̸=0$即${\alpha }_n$>0的点，得到$1-y_n(w^T{z}_n+b)=0$，进而求得$b=y_n-w^T{z}_n$。

值得注意的是，计算b值，${\alpha }_n$>0时，有$y_n(w^T{z}_n+b)=1$成立。$y_n(w^T{z}_n+b)=1$正好表示的是该点在SVM分类线上，即fat boundary。也就是说，满足${\alpha }_n$>0的点一定落在fat boundary上，这些点就是Support Vector。这是一个非常有趣的特性。