本篇是 TreeMap 和红黑树源码分析的最后一篇了,这次会结合 TreeMap 的源码教大家红黑树删除节点的算法。红黑树的删除算法要比插入更为复杂些,但是也不必担心,本文会用简单明了的解释,并结合 JDK 的源码让你了解红黑树的删除算法。
在正文开始之前,还请大家确保自己理解之前两篇文章中讲述的知识点,如果有些遗忘也不妨再次快速的复习一下。
Java Collections Framework 源码分析(5.1 - Map, TreeMap, 红黑树)
Java Collections Framework 源码分析(5.2 - TreeMap, 红黑树的插入)
TreeMap 的 remove 方法
Map 上的 remove 方法的作用是从容器内移除键值对,我们先看一下 TreeMap 上的实现:
public V remove(Object key) {
Entry p = getEntry(key);
if (p == null)
return null;
V oldValue = p.value;
deleteEntry(p);
return oldValue;
} 通过 getEntry 方法从红黑树中获取对应的 Entry 对象,如果对应 key 的 Entry 不存在则直接返回 null。否则会执行 deleteEntry 方法,并将返回旧的值。让我们继续往下看 deleteEntry 方法的实现。
deleteEntry
从 deleteEntry 的代码来看主要分为两个部分:
- 从红黑树(平衡二叉树)中删除节点。
- 重新调整树的状态,恢复平衡。
让我们先了解一下平衡二叉树删除节点的算法,具体算法其实很简单,需要区分两种不同的状态。我们先说简单的,如果当前删除的节点只有一个非空子节点,那么只需要直接删除就行了,即把自己子节点和父节点建立连接关系即可。而当自己有两个非空子节点时,则需要按照下面的顺序进行删除操作:
- 找到当前删除节点的的前驱节点或是后继节点(前驱与后继的概念稍后会说)。
- 将前驱(或是后继)节点的值复制给需要删除的节点
- 按照第一种情况删除那个前驱(或是后继)节点
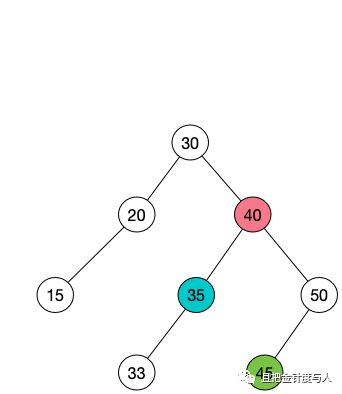
在详细解释之前,我们先说前驱和后继的概念。因为平衡二叉树实质上是一种排序的数据结构,如果把它拉成一条直线,其实就是一个链表。而前驱的意思就是小于且最接近当前节点的节点,相应的后继就是大于且最接近的节点,具体可以看下面的图:
假设图中40(红色)的节点为当前节点,那么35(蓝色)节点为前驱节点,45(绿色)节点为后继节点。
了解了这些背景知识之后,可以看一下 deleteEntry 的代码了。
// If strictly internal, copy successor's element to p and then make p
// point to successor.
if (p.left != null && p.right != null) {
Entry s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
} // p has 2 children 这部分代码按照我们之前所说的算法,先执行了有两个非空子节点情况下的逻辑,同时这里选择的是使用 successor 后继节点进行替换。很容易看出在使用 successor 获得当前节点的后继节点后,将后继节点的值复制给了当前节点,然后将需要删除节点的引用指向了后继节点。
successor 方法我就不在解释了,我建议你可以去看一下,看看是否符合我们之前的定义。相应的,在 TreeMap 的源码中还有一个 predecessor 方法是获取当前节点前驱节点,也值得看一下。
然后我们接着往下看:
// Start fixup at replacement node, if it exists.
Entry replacement = (p.left != null ? p.left : p.right);
if (replacement != null) {
// Link replacement to parent
replacement.parent = p.parent;
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
// Null out links so they are OK to use by fixAfterDeletion.
p.left = p.right = p.parent = null;
// Fix replacement
if (p.color == BLACK)
fixAfterDeletion(replacement);
} 这里是进行节点删除的具体代码,此时需要删除的 P 节点有可能已经是指向后继节点了,但是无论如何,删除的逻辑都是一样的,都是重新建立父节点与子节点之间的关联,并移除与要删除节点间的关联。至此第一步删除节点的操作已经完成了,接下来就是要对树进行重新平衡,以符合红黑树的要求。
fixAfterDeletion
从上面代码片段中可以看出,在进行节点删除之后,调用了 fixAfterDeletion 方法,还记得上一篇中有个类似的 fixAfterInsertion 吗?不难猜出,这个 fixAfterDeletion 就是在删除节点后对二叉树重新平衡的方法,让我们先参考 wiki 上的算法定义。
相对插入而言删除的算法稍微更复杂些,需要执行 6 步操作。但也不用慌,耐心往下看(算法描述依然采用之前的 N,P 等缩写)。
- N 是否为根节点,如果是,那么就直接终止,否则执行第 2 步操作。
-
S 节点,如果 S 节点颜色为红色:
- P 改为红色
- S 改为黑色
-
N 是否为 P 的左节点
- 是:将 P 左转
- 否:将 P 右转
执行第 3 步操作
-
P,S,S.left,S.right 这些节点的颜色都为黑色:
- S 改为红色
- 将 P 作为参数,从第 1 步开始重新执行
否则执行第 4 步
-
P 为红色,S,S.left,S.right 都为黑色:
- S 改为红色
- P 改为黑色
- 终止操作
否则执行第 5 步
-
S 的颜色为黑色
-
N 为 P 的左节点,S.right 为黑色,S.left 为红色
- S 改为红色
- S.left 改为黑色
- 将 S 右转
-
N 为 P 的右节点,S.right 为红色,S.left 为黑色
- S 改为红色
- S.right 改为黑色
- 将 S 左转
-
执行第 6 步操作
- 将 S 的颜色改为 P 的颜色
P 改为黑色
1. N 为 P 的左节点
1. S.right 改为黑色
2. 将 P 左转
2. N 为 P 的右节点
1. S.left 改为黑色
2. 将 P 右转
上手一看算法逻辑可能很繁琐,其实仔细看一下,很多都是对称的,你只需要记住一半就行了。现在结合 TreeMap 的代码看一下:
private void fixAfterDeletion(Entry x) {
while (x != root && colorOf(x) == BLACK) {
if (x == leftOf(parentOf(x))) {
Entry sib = rightOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateLeft(parentOf(x));
sib = rightOf(parentOf(x));
}
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
x = root;
}
}
...... 可以看到 fixAfterDeletetion 方法的逻辑与我们描述的算法在顺序上稍有不同,它在一开始的分支条件是区分当前节点是左节点还是右节点。紧接着的:
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateLeft(parentOf(x));
sib = rightOf(parentOf(x));
}这部分可以看到对应我们算法的第 2 步。需要注意的是 sib = rightOf(parentOf(x));,那是因为发生旋转后,sib 也发生了变化,需要重新获取。接下来的:
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
}也能看到是对应算法的第 3 步,将 x 设为了 parent,然后重新开始 while 循环。之后的分支也都可以对应到算法的剩余步骤,我把这部分代码解读的工作流给你了,不妨自己拿笔和纸出来,将代码和我所描述的算法一一对应,看看能不能对上。
结语
至此,TreeMap 和红黑树的所有代码都分析完了。最后这篇节点删除算法拖了很久,期间有人也私信问我,为什么要学习红黑树?为什么要学习数据结构?我们工作中就是 CRUD ,什么排序,什么查找,都是用现成的呀,有问题吗?这是个很有趣的问题,在我工作过程中有很多人问过我类似的问题,可以把数据结构和红黑树替换成其他的许多名词,例如操作系统,编译原理,JVM 等等,等等。我想后面会花时间用一篇单独的文章来回答这个,而在这里我只想说对于这些底层知识的掌握,决定了你能力的上限,换而言之也决定了你能做什么和不能做什么 。
接下来应该是 Java Collections Framework 最后一部分了,也就是 HashMap 的源码解析,希望你不要错过。
欢迎关注我的微信号「且把金针度与人」,获取更多高质量文章![]()