《Think Python》练习 4-2：用函数画花朵

第4章 案例研究：接口设计

练习 4-2 用函数画花朵

写一组合适的通用函数，用来画出下图所示的花朵图案（最终代码执行效果图）：

【求解】
Step.1 确认组件
如果想通过本张介绍的多边线 polyline(t, n, length, angle) 和弧函数 arc(t, r, angle) 画出花瓣的弧，需要知道：花瓣的弧度和弧长

#多边线
def polyline(t, n, length, angle):
    for i in range(n):
        t.fd(length)
        t.lt(angle)
        
#弧
def arc(t, r, angle):
    arc_length = 2 * math.pi * r * abs(angle) / 360
    n = int(arc_length / 4) + 3
    step_length = arc_length / n
    step_angle = float(angle) / n
    t.lt(step_angle/2)
    polyline(t, n, step_length, step_angle)
    t.rt(step_angle/2)

Step.2 抽象问题
已知：花瓣瓣数 $n$，花瓣长度 $l$
求：花瓣的弧度和弧长（ polyline(t, n, length, angle) 中的 angle 和 length）

Step.3 问题求解
观察花朵：对于花瓣 不重叠 的花朵，花瓣越多，花瓣越细
故，设：组成花瓣的弧线的弧度（angle）为 $\frac{2\pi }{n}$，以实现“花瓣越多，花瓣越细”的效果
由于在弧度单位下 $l=|\alpha |r$，故还需要知道花瓣弧半径 $r$ 才能计算弧长（length）

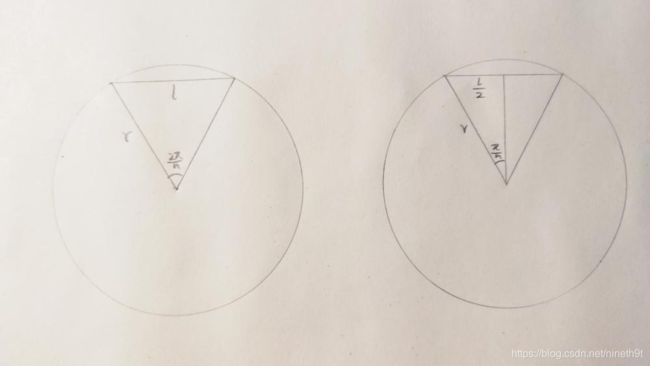
由上图求$r$：
$$r=\frac{l}{2sin\frac{\pi }{n}}$$
由公式 $l=|\alpha |r$，求弧长length：
$$length=\frac{\pi l}{nsin\frac{\pi }{n}}$$
此时通过 arc(t, r, angle) 可以画出花瓣的一条弧，还需要要转一个角度再画出同样的一条弧，这个角度是花瓣尖角，两条弧相交点的切线夹角，由于花瓣尖角里外相同，每个花瓣尖角也相同，故这个花瓣尖角是根据花瓣数量平分 $360°$：$\frac{360°}{n}$，转角是花瓣尖角的补角$180°-\frac{360°}{n}$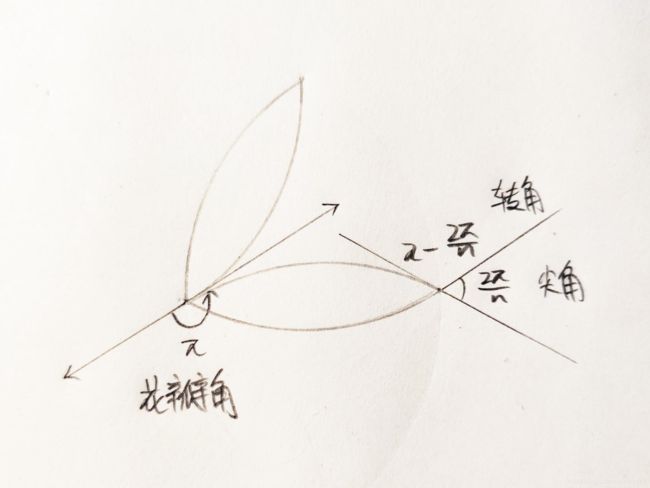
同时上一个花瓣终点的切线和下一个花瓣起点的切线重合，画完上一个花瓣后，需要转向 $180°$ 继续画下一个花瓣：

"""
《Think Python》练习 4-2：用函数画花朵

l：花瓣的长度(花朵的直径)
m：花瓣的个数
"""

#引入数学模块、乌龟模块
import math
import turtle

#调用乌龟画图、提高画弧速度
bob = turtle.Turtle()
bob.delya = 0.01

#多边线
def polyline(t, n, length, angle):
    for i in range(n):
        t.fd(length)
        t.lt(angle)

#弧
def arc(t, angle, arc_length):
    #计算：弧分几段画，每段多长，每段之间的夹角
    n = int(arc_length / 4) + 3
    step_length = arc_length / n
    step_angle = float(angle) / n
    #画出弧
    t.lt(step_angle/2)
    polyline(t, n, step_length, step_angle)
    t.rt(step_angle/2)

#不重叠花瓣的花朵
def flower(l,m):
    #计算：弧度、弧半径、弧长
    arc_angle = 2 * math.pi / m
    arc_angle2 = 360 / m
    arc_r = l / 2 / math.sin(arc_angle/2)
    arc_length = arc_angle * arc_r
    #计算：花瓣尖转角度数
    angel = 180 - 360.0/m
    #画出花朵
    for i in range(m):
        arc(bob, arc_angle2, arc_length)
        bob.lt(angel)
        arc(bob, arc_angle2, arc_length)
        bob.lt(180)

注意：计算三角弧度单位是弧度（arc_angle = 2 * math.pi / m），乌龟转向单位是度数（arc_angle2 = 360 / m）

对于 花瓣重叠 的花朵，如果其花瓣是 $2n$，实际上是画一个花瓣为 $n$ 且不重叠的花朵，转半个花瓣尖转角度数（angel = 180 - 360.0/m）再画一朵完全一样的花朵：
至于我为什么知道？完全因为小时候看《百变小樱》的时候，给自己画了个“魔法阵”，就是上图?

#重叠花瓣的花朵
def flower2(l,n):
    m = int(n/2)
    flower(l,m)
    bob.lt(180/m)
    flower(l,m)
    bob.rt(180/m)

Step.4 完成代码

"""
《Think Python》练习 4-2：通用函数画花朵

l：花瓣的长度(花朵的直径)
m：花瓣的个数
"""

#引入数学模块、乌龟模块
import math
import turtle

#调用乌龟画图、提高画弧速度
bob = turtle.Turtle()
bob.delya = 0.01

#多边线
def polyline(t, n, length, angle):
    for i in range(n):
        t.fd(length)
        t.lt(angle)

#弧
def arc(t, angle, arc_length):
    #计算：弧分几段画，每段多长，每段之间的夹角
    n = int(arc_length / 4) + 3
    step_length = arc_length / n
    step_angle = float(angle) / n
    #画出弧
    t.lt(step_angle/2)
    polyline(t, n, step_length, step_angle)
    t.rt(step_angle/2)

#不重叠花瓣的花朵
def flower(l,m):
    #计算：弧度、弧半径、弧长
    arc_angle = 2 * math.pi / m
    arc_angle2 = 360 / m
    arc_r = l / 2 / math.sin(arc_angle/2)
    arc_length = arc_angle * arc_r
    #计算：花瓣尖转角度数
    angel = 180 - 360.0/m
    #画出花朵
    for i in range(m):
        arc(bob, arc_angle2, arc_length)
        bob.lt(angel)
        arc(bob, arc_angle2, arc_length)
        bob.lt(180)

#重叠花瓣的花朵
def flower2(l,n):
    m = int(n/2)
    flower(l,m)
    bob.lt(180/m)
    flower(l,m)
    bob.rt(180/m)

#左移240，画出不重叠花瓣的7瓣花
bob.pu()
bob.fd(-240)
bob.pd()
flower(100,7)

#右移240，画出重叠花瓣的10瓣花
bob.pu()
bob.fd(240)
bob.pd()
flower2(100,10)

#左移240，画出不重叠花瓣的20瓣花
bob.pu()
bob.fd(240)
bob.pd()
flower(100,20)

#下移120，让turtle不遮挡花朵
bob.pu()
bob.rt(90)
bob.fd(120)

turtle.mainloop()