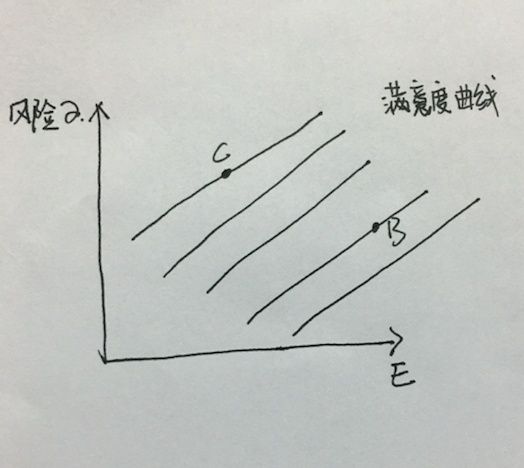
在上一篇文章中我们学习了一下无差别曲线以及一些理财原则,在上边的讨论我们其实都是定性的讨论而不是定量的讨论,那接下来我们将会继续在上文的曲线中取回无差别曲线,顺便请回我们的老朋友B,C点来进行讨论,C点和B点坐落在不同的满意度曲线上,因为他们是可以明显比较的,并且我们知道,满意度曲线越往下,是越满意.
接下来我们要讨论的一个问题是,那么如果我们现在所有的投资组合全部投资去C,那么我们这个投资的风险和回报是否会和C点完全重合?因为他是C点,肯定是这样的选择,如果我们全部投资B,那么现在这个肯定也是百分百的选择,那现在我们是以不同的配比,比如说99%投B,1%投C,那么这个是不是一种新的投资分配方案?而这个新的投资方案能不能来考虑他风险和回报?
答案是可以,因为这本身也是一种投资,所以我们可以去讨论这个问题,另外从刚才的图中来看,这个分配方案的坐标也是坐落在这个坐标平面的一个点,那接下来我们简单的理解一下下面这个混搭的问题,就是一旦我们把他进行混搭以后,新的点会坐落在什么样的位置,比如说我们把B,C两点连成一条直线.现在就有一个新的问题,混搭之后不同比例的点作为一种投资,这个点会坐落在这条直线上么?看起来有点可能,因为如果我们用极限思想的话,百分百是B就跟B重合,百分百C就跟C重合,但是事实上,不是直线,而是一条下移的线.
为什么?
因为收益就像取平均值一样,他是有线性叠加性的,而风险他会对重,说一个简单的例子,我们去投一个硬币,我们先考虑一个简单的模型,投硬币一旦投到上面,我得到一块钱,投硬币得到下面,我得到0元
那这时候我这样的投资,我的收益是多少?收益的期望是0.5对么?我的方差是0.25,但是我们不在乎数字,因为这一次分析是纯定性的,定量的话就真的要开始铺垫我们的数学了,一旦我们知道这个平均值和方差之后,他作为一个投资就就假设为这样,那接下来我们不投一个硬币,把向上的部分叫做A投资,把向下的部分叫做B投资,我们把A投资玩两次,第一次叫A,第二次叫A’,如果你开心的话你可以玩多少次都OK,然后投10次在去除以10,这相当于是各以1/10的概率,进入不同投资的新的投资方式,而这个新的投资方式,所占用的资金还和原来还是一样,那他的这一次新的投资的期望还是0.5,因为你丢一次硬币的期望是0.5,你丢10次然后累加,然后每一个期望是0.5/10加起来还是0.5,但是方差却远远地缩小了,你只有投10次都是正面或者投10次都是负面的时候,你才能够还原之前的方差,否则的话因为这几个投资之间是独立的事件,否则他的方差会变小,也就是说你很难有很大的概率去偏移0.5,你平均一次的真实的期望,是一个1/(根号n)的一个关系去缩减(必须是独立事件,跟分布无关,而这个事 件我们不去证明,我们只是当做一个数学结论拿来用,就是你丢10次硬币,你很难让平均值偏离0.5太多),那这样的话说明,如果事件是独立的话,那么风险是会对冲的,那么回到我们上边的满意度图中,只要BC这两个渠道,只要他们的相关性不是1的话,他都会对冲掉一定的风险,如果他们是完全不相关,他会对冲掉比较大的风险,有一定的相关性,他会对冲掉少一点的风险,什么是完全不相 关呢?比如说德州的天气会直接导致德州的庄稼的收成,那么这算是一种投资对不对,我们把钱来投资德州的农业,这是一种风险,那这个德州天气的风险跟加州会不会独立,这就是一个相对独立的事件,但是德州天气的风险跟加州天气的风险的相关性就会稍微多一点点,你不能说他是完全正相关还是完全无关,就是说两个投资之间是相互独立的话,他们之间的对冲就会比较多,如果不太独立,对冲就会相对比较少.
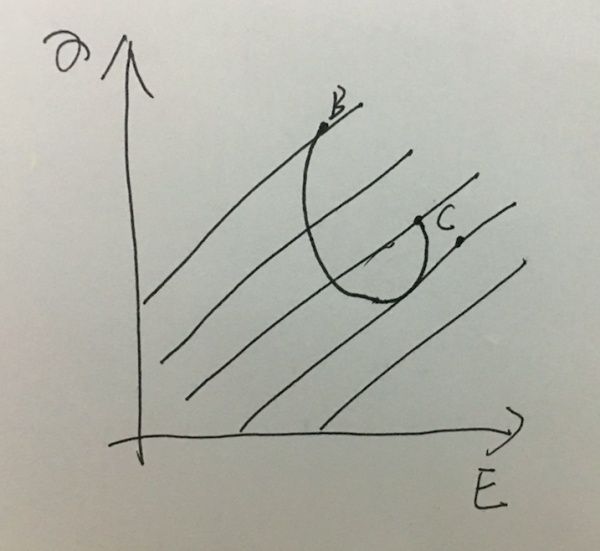
如果用一个定性的方式来去理解的话,如果他独立就可能成为一个①的状态,如果对冲成中间的一个过渡分布的话,就会形成一个②的情况,如果他完全相关,并且相关系数是1,他就会回归成一条直线,也就是说在BC之间,你以不同的配比进行投资的话,你能够改变你的配比画出一条连续的线来,并且这个线是往下的.
那这个时候,有趣的事情来了,我们刚才说满意度,我们上边每一个点都能实现一个精确地数值,并且呈现出一个不同的曲线在下方,但是因为满意度曲线越往右下越满意,所以你能够在所有的满意度曲线里取到一个跟满意度曲线相切的一条曲线,就是你能取到最下面的满意度曲线,并且它的满意度是大于B的(如果从数学上来说,就是要涉及到你整体的无差别曲线是什么样,如果你的无差别曲线的斜率刚好跟BC这条线是垂直的话,你这样的一排曲线最右下边的点还 是B点,但是这样的情况是比较小的,什么情况下能够突破B这个满意度的情况呢?一个是BC之间的相关性越小越能突破,还有一个是你的风险偏好,一般来说很难出现,因为我们几乎可以认为,当我们百分之百的把钱放到一个地方的时候,是值得慎重考虑的,就从上边的图我们也能看出来,配比也不会百分之百或者是大部分放到C,大部分还是放到我们认为靠谱的投资渠道,但是不要完全相信他,还是要分散风险). 而这样的定性的思维,我们还可以定性的叠加,就是说你现在的所有的投资渠道,只有两个话,我们可以混搭出一个N的投资渠道,但是你在这个世界上你有发现了一个新的投资渠道叫做M的话,那么这两者之间又可以产生新的不同的配比,又可以画出更加没有下限的满意度曲线,所以就是说一旦出现新的投资渠道,你就又一次可以不断地优化的你的投资配置,而整体投资配置这件事情是可以不断配置的,而作为一个投资经理,他要去寻觅这个世界上尽可能多的投资渠道去优化他的投资组合,除非他的基金被限制在某一个特殊的领域,比如说中国的股票基金,他的基金经理的选择方式只能是那些股票,但是像是一些主权基金,他就会投资非常分散,就跟哈弗大学的投资基金,他的投资就是非常分散的(大家有兴趣可以看看,有一个饼图,高度分散的投资领域).
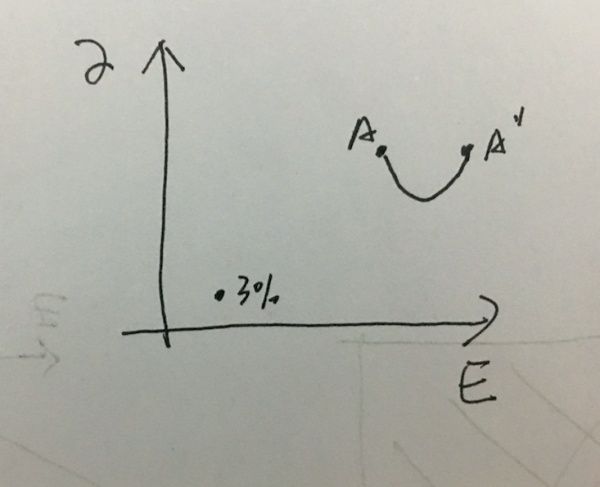
说一个简单的例子:
如果我们看看银行的投资,首先银行的期望很小,年利率是3%假设,然后他的风险非常小,那这时候我们觉得这是普通市民都可以找得到的投资方式,但是索罗斯找到了一个英国脱欧的机会,这时候他去对赌,这时候他的收益可能是50%,当然他也承担这很大的风险,,他又找到另外一个,可能也是投资收益很大,但是风险也会很大的投资,那么他这两个风险一配比,他就能拉出一个风险,比各自单独的风险小的多的一个东西.然后如果再找到一个A’’.甚至可以再去降低风险,他最后可能会获得风险会和银行差不多,但是收益比银行高到不知道哪里去了的一个投资配比,因为期望的平均值是等于平均的期望,但是风险会对冲.而这一切都是由大数定律来保障的.