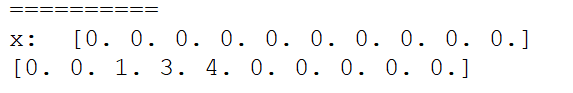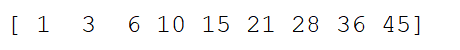numpy汇总笔记

numpy汇总笔记

numpy：

python处理矩阵数据的最常用工具，几乎所有的框架都会保留numpy转换的接口，所以在进一步学习深度学习之前，对numpy做一个汇总学习是十分必要的；

在对numpy的再一次学习当中，将numpy大致总结为以下五点：

1. 数组形状操作（创建，切片，合并分割，变形）
2. 索引（花哨索引，掩码）
3. 通用函数（运算符，广播，聚合）
4. 结构化数组
5. 其他

数组形状操作

数组的形状操作大概包括3点：数组的创建，数组的切片，数组形状的改变，以及合并分割；

numpy数组的创建

• 从python列表创建
• numpy自带的数组创建函数

从python列表创建

x = np.array(L)

L是python当中的列表，numpy数组能直接通过python的列表进行创建，同时可以直接指定数组元素的类型，对数组元素中不符合的进行默认转换：例如

x = [1,2.0,3.4]
x_2 = np.array(x,dtype=int)
print(x_2)

[1,2,3]

如果不指定dtype，numpy就会自动确定其元素类型为列表当中最复杂的那一个类型，

注意：numpy可以通过包含字符串元素的列表进行创建，但是也就相应的这个numpy数组不能进行任何计算，没有意义，并且这种情况，程序只会提前返回，不会报错；只会有如下提示：

numpy自带的数组创建函数

自带函数主要分为两类，一类是从0创建数组，一类是依据别的数组创建数组

（1）指定范围有序建立系列

从begin点到end点有序取点

• np.arange(begin,end,step)
• np.linespace(begin,end,number)
  小知识点：1.arange不包含end点，而linespace包含了end;2.arange的step默认是1；

（2） random系列

• np.random.random(shape) // 创建shape形状的数组，元素为0到1均匀分布的随机数值
• np.random.normal(mean,var,shape) // 均值为mean，方差为var的标准正态分布数组
• np.random.randint(begin,end,shape)//创建begin到end之间的随机正整数数组
• np.random.randn(shape)//默认生成[0，1）之间的标准正太分布数组
• np.random.rand(shape)//只是[0，1）之间的随机样本数组

（3）一些特殊的

• np.eye(number) // 创建一个number*number的单位矩阵
• np.empty(shape) // 创建一个shape数组，其中的值由内存中存在值随机确定；
• np.zeros_like(X) // 创建一个shape和X相同的0数组

数组切片

与python中列表的切片操作一致，每个维度用[start:stop:step]格式进行切分，弱不传，start默认为最开始，stop默认为结尾，step默认1，同时不包含stop位置元素，但是包含start位置元素；

小知识点：1.切片不包含stop位置元素，想要切分到结尾，需要使用不传stop，让它使用默认值；2.numpy的切分属于视图操作——改变切片当中的元素，原本数组当中的元素也会发生改变；

数组的变形

简单的说就是对数组的维度进行改变，reshape就是它最常用的方法

numpy数组的变形只有两种方式：

• np.newaxis
• resahpe(shape)
  （1）reshape方法最为简单：在reshape参数中传入一个shape参数，直接就会返回一个原来数组的shape形状的视图，重点，这里只是视图操作；
  （2）np.newaxis方法主要是和切片进行组合操作；例如
  原本数组A是一个（3，1）的形状，现在想把她变成（1，3，1）,只需要
  A = [np.newaxis，:，:]这样就获得了A的（1，3，1）视图,记住也只是视图；

数组的合并分割

将数组根据索引位置划分为多个数组或者多个数组合并为一个数组

数组的合并：

• np.concatenate([A,B],axis)
• np.vstack
• np.hstack
• np.dstack

数组的分割：

• np.split(A,[a,b…],axis)
• np.vsplit
• np.hsplit
• np.dsplit

合并函数将多个数组按照需要操作的axis进行合并，比如如果axis=0，则合并的时候操作的是增加行（即第一个维度）；而分割的时候将数组A按照第二个列表当中的元素在对的axis进行分割，比如axis=0，则将前a行给数组一，这样依次划分；
对numpy中的axis的理解是一个比较难理解的点，但是每次使用的时候，强化记忆，它是指折叠的axis，而不是返回的axis就行，多记忆；

索引

numpy的索引完全继承了python的索引，并在此基础上增加了多维索引的新的方式；

多维数组索引新的方式：

对于二维数组A，获取其1行1列的数据，在python当中只能A[0][0]这样进行获取，而在numpy数组中不仅可以这样获取，而且可以用A[0,0]这样的方式；

花哨索引

numpy数组在python基础上新增的一种索引方式，它可以在中括号当中传入一个数组来操作批量数据；

例子：

print("==========")
x = np.arange(9)
np.random.shuffle(x)
print("x: ",x)
indices = [1,3,0]
print("indices: ",indices)
print("x[indices]: ",x[indices])

输出：

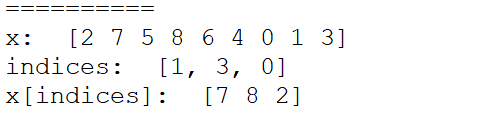
可以看到，numpy数组能直接传入索引数组，并且获得索引数组形状的数据视图显示
小重点：numpy的索引可以和其他索引方式（切片，掩码，普通索引）进行任何形式的组合使用；
小知识点：当索引数组当中存在相同的索引时，如果对其进行加一操作，最后的结果可能并不会如我们所想；
例如

print("==========")
x= np.zeros(10)
print("x: ",x)
indices = [2,3,3,3,4,4,4,4]
x[indices] += 1
print(x)

输出

以为会因为有3个3的索引，就会对3索引位置的值进行3次加一操作，但是事实上并没有，其原因可能是因为多次加一同时执行，和线程安全有一定关系（瞎猜），要实现这样的多次加一（通过索引数组），操作，numpy中内置了np.add.at（x,indices,1）函数——at函数是部分运算通用函数可以调出的针对这种情况的专用函数，不止是在add中才有；
add.at函数使用实例：

print("==========")
x= np.zeros(10)
print("x: ",x)
indices = [2,3,3,3,4,4,4,4]
np.add.at(x,indices,1)
print(x)

输出：

花哨索引和其他索引方式的组合

（1）这些组合很多，但是大体上记住一点就行，numpy数组的花哨索引很灵活；
（2）像A[:,indices],A[1,indices]这样的组合都可以使用；

掩码

在引入掩码的概念时，首先要了解numpy的比较操作，然后是numpy的逻辑与或非操作，最后再是掩码操作；

numpy比较操作

numpy支持6种比较操作：<，>，>=，<=，==，!=;

numpy数组和的比较和其其他的运算规则是一致的，比如一个数组和一个数值做比较，他会让整个数组和这个数值进行比较（联想numpy的广播特性，后面会对广播特性进行总结）,最后返回一个bool数组:
例如：

x = np.array([[1,2,3],[4,5,6],[7,8,9]])
y = x > 4
print(y)

输出：

numpy的逻辑与或实现

上面的例子当中实现了x>4的bool运算，那么要实现8>x>4要如何实现呢？

我们很容易联想到and操作：
y = x > 4 && x < 8
让我们看看会发生什么：

x = np.array([[1,2,3],[4,5,6],[7,8,9]])
y = x > 4 && x < 8
print(y)

输出：

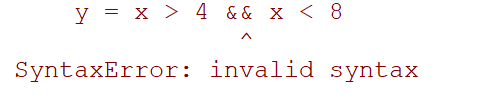
没错会报错，再numpy种要实现多条件需要使用bool运算逻辑；

x = np.array([[1,2,3],[4,5,6],[7,8,9]])
y = (x > 4) & (x < 8)
print(y)

输出：

其原理其实也是矩阵运算，numpy将（x>4）bool矩阵和（x<8）矩阵进行了bool运算的&运算，python中，True代表一个比特位1，False代表比特位0;

numpy掩码

顾名思义不显式的暴露出索引位置，和numpy的花哨索引类似，不过在中括号中传入的不再是索引数组，而是bool数组；

例如：
上面的bool数组y：

将y传入x中括号运算内：x[y]:
输出：

没错，只返回了为True的那些对应的值；
掩码操作通常传入的是和数组相同形状的bool数组作为掩码，最终将bool数组中True对应原数组的元素作为一个列表进行返回；

通用函数

即对所有numpy数组都可以调用的函数——numpy通用函数

• 数组运算
• 聚合运算
• 广播特性

数组运算

numpy的数组运算，类似于加减乘除，bool运算的操作都是自动对整个数组进行操作，他们都分别对应了相应的通用函数，联想C++中的重载运算符；

函数	numpy对应的函数
运算符	+，-，*，/，-(取反)，//，%
三角函数	np.sin,np.cos,np.tan.np.arcsin…
指数和对数	np.exp,np.exp2,np.power,np.log,np.log2…
e^x-1	np.expm1
log(x+1)	np.log1p
其他的	查阅numpy文档和scipy文档

更多的通用函数——更复杂的函数实现都被放在了Scipy的special模块中,如果有需求的话，可以查看相关的文档，其中实现了广义阶乘Gamma函数以及误差函数（高斯积分）等等

聚合运算

将整个数组的部分或全部元素像求和或者求乘积这样‘聚合’成一个或几个数值；

numpy的聚合函数主要有两种方式：

• 通用函数的reduce方法和accumulate方法
• 内置的通用聚合函数

reduce和accumulate方法

这两个通用函数的方法都只是部分的通用函数才会有，已知的有add，multiply和substract(减)三个方法；

reduce举例：(获得通用函数对整个数组或部分数组元素的通用函数操作)

print("==========")
x = np.array([[1,2,3],[4,5,6],[7,8,9]])`在这里插入代码片`
y = np.add.reduce(x)
print(y)

输出:

reduce默认对axis=0的情况进行了列全部相加操作，当然这个axis是可以改变的；
这里的例子只是对多维数组的操作，如果对一维数组，则，reduce方法会直接返回所有元素的操作结果，另外reduce想对多维数组进行全部元素操作的话，可以对axis传入一个元组，包含所有的维度就行：

print("==========")
x = np.array([[1,2,3],[4,5,6],[7,8,9]])
y = np.add.reduce(x,axis=(0,1))
print(y)

输出：

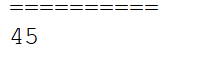
accumulate举例：（将初始值和过程中所有会出现的中间值都保存在一个数组里面进行返回）

print("==========")
x = np.array([1,2,3,4,5,6,7,8,9])
y = np.add.accumulate(x)
print(y)

输出：

内置的聚合函数

当然他们都是可以指定维度的，这些函数默认的axis是包含所有维度

numpy聚合函数和它们的NaN安全版本¹：

聚合函数	NaN安全版本
np.sum	np.nansum
np.prod	np.nanprod
np.mean	np.nanmean
np.std	np.nanstd
np.var	np.nanvar
np.min	np.nanmin
np.max	np.nanmax
np.argmin	np.nanargmin
np.argmax	np.nanargmax
np.median	np.nanmedian
np.percentile	np.nanpercentile
np.any	np.nanany
np.all	np.nanall

小知识：np.any(x)，是判断x数组中是否存在真值；np.all是判断是否全部是真值；最后一个percentile函数，要额外传入一个q值，当q=50的时候，这个函数相当于返回中位数；当然也可以传其他的百分比；

广播特性

还记得numpy数组原本的对数组加上一个数值最后返回一个矩阵加上该数值的操作吗？

numpy的广播特性就是考虑了很多时候可能要对不同shape的数据进行计算所参生的特性，从概念上理解它就是先通过一定的规则，将两个数组的shape变成一致之后再对两个数组进行计算；
举例：

x = np .array([1,2,3])
y = np .array([[4],[5],[6]])
print(y+x)

输出：

这是怎么得到的呢？
先看numpy的广播转换规则:

（1）如果两个数组的维度数量不相同，那么维度少的数组就会在维度少的数组的形状最左边加上一个维度；
（2）如果两个数组的形状在维度上不匹配，那么数组的形状会沿着维度为1的维度扩展来匹配另一个数组；
（3）如果维度不匹配且没有维度为1的维度，那么报错；

因此，上面的x的shape是（3，），而y的shape是（3，1），根据第一条规则，在x的shape左边维度加一，那么x变成（1，3），再根据第二条规则，把两个数组都变成（3，3），最终进行相加，其中x的假想图为：
x=[ [1,2,3],
[1,2,3],
[1,2,3] ]
因为是从[[1,2,3]]扩展行，后面扩展的行和最初的行元素都是相同的，对两个数组进行这样规则的概念转换后相加，也就得到了最后的结果：

结构化数组

numpy用于存储关联数据的方式：此种方式可以传入一个数据，该数据又包含很多属性数据；

最简单的举例：
一个学生的数据有姓名，身高和年龄，如果我们将它们分布存储，各个数据之间就没有任何的关联性了，numpy要实现类似于josn格式的数据，也就是采用这样的格式；

numpy创建结构化数组的方式主要是对dtype的指定，而dtype的定义方式主要有三种：

• 采用字典的方式对’name’和‘format’两个字段进行赋值，例：dtype={‘name’: (‘name’,‘age’,‘weight’),‘format’: (‘U10’,‘i4’,‘f8’)}
• 采用元组列表的方式：例如：dtype=[(‘name’,‘s10’,(‘age’,‘i4’),(‘weight’,‘f8’))]
• 只指定元素类型的方式，这种方式元素的类型名将会又系统创建；例如：dtype=‘s10,i4,f8’

记录数组

使用结构化数组中的通用方法view传入**np.recarray**获得，获得之后，对每个数据的属性获取就可以之间点操作就能获取，非常方便，但也同样的付出代价，速度会变得很慢；

例：

tp = np.dtype([('name','S10'),('age','i4')])
x = np.zeros(5,dtype=tp)
x = x.view(np.recarray)
x[0].name = 'dj'
print(x)
print(x[0].name)
print(x['name'][0])

输出：

所以是否要使用这种方式需要慎重考虑，其实现也主要是view(np.recarray)，最后调用的速度会变慢，即使不使用调用属性的方式；

pandas就是基于numpy的结构化数组的基础上建立的；

其他

最后是一些numpy库使用中比较纠结的点和一些不容易注意的知识点

numpy数组的6个有用的属性

属性名	意义
ndim	数组一共有多少维度
shape	数组每个维度的大小
size	数组元素的总数
dtype	数组元素的类型
itemsize	每个元素所占字节
nbytes	数组总共所占用的字节

numpy数组插入不同类型的值和python数组插入不同类型的值，其反应的区别

python的数组里面会直接报错，而numpy会对数据进行截短或者补位，例如如果将3.9传入整型数组当中，python会报错，而numpy会将数据变成3传入，记住是3，并不是四舍五入，只是简单的截断；

副本和视图的区别

得到副本的话，相当于系统已经做了copy操作，在获得的副本上操作并不是改变原来的数据，而视图相反，并没有系统调用copy，它的改变会直接影响原来的数据；当然要实现副本也很简单，在视图后面点copy()就可以获得；

numpy数组操作中哪些是副本，哪些是视图操作

视图：

• 切片
• reshape和np.newaxis
• split

副本：

• concatenate（合并）

注意这里的数组的分割是视图，合并是副本，记住了;

numpy的axis问题

numpy的axis指的是要被折叠的维度，不是返回的维度，不管是排序，聚合，分割都是如此；

numpy通用函数的out参数

out参数如果指定了位置，那么程序的计算就会直接在该位置输入，会直接略掉中间的临时值copy过程，例如A = np.power(A,2),这个函数实际执行过程中会首先创建一个临时值报存结果，然后再传给A，而使用了out参数的话，程序会直接传给out参数指定的位置，在数据量比较大的时候，可以进行考虑；

numpy通用函数的outer方法

用于返回两个数组各个元素进行计算之后的结果；

例如：

x = np.arange(10)
y = np.add.outer(x,x)
print(y)

输出:

其结果就是把x中每个元素与另一个x中每个元素相加，最后的结果数组；

numpy通用函数的快速性（比python本身快）

这也是为什么要使用通用函数的原因，很多numpy的函数，python中也有，但是numpy的会比python的快速很多；其原因是因为numpy不用保留数据元素的灵活性，每次只需要调用同一个函数，而py会对元素的类型进行判断，再判断该类型所需要的函数；

np.searchsorted(A1,A2)函数和np.histogram(A1,A2)函数

1. 这两个函数一般使用时需要将第一个参数的数组传入有序数组
2. searchsorted函数会返回一个索引数组，对应A2中元素要插入A1中，需要插入的索引位置；
3. np.histogram函数的运算速度很快，其会返回两个数组，实现和searchsorted函数类似的功能，在matpyplot的hist画图方法中，就会默认调用这个方法；
4. histogram函数返回的第一个数组是一个计数数组，指A2中元素在A1各个区间的个数，而第二个数组就是返回的各个区间的边缘值；

---

1. 在对有缺失值的数组进行计算时，如果不使用NaN安全版本，就会报错，NaN缺失值即特殊的IEEE浮点型NaN值，在使用安全版本时计算会直接忽略这些NaN值； ↩︎