单调栈(总结+例题)
定义:单调栈,顾名思义,是栈内元素保持一定单调性(单调递增或单调递减)的栈。这里的单调递增或递减是指的从栈顶到栈底单调递增或递减。既然是栈,就满足后进先出的特点。与之相对应的是单调队列。
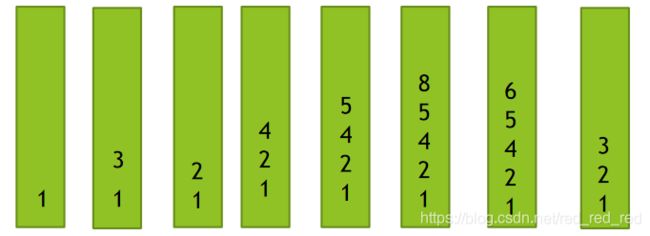
入栈操作: 1,3,2,4,5,8,6,3(单调递增栈)
则如果栈为空或入栈元素值小于栈顶元素值,则入栈;否则,如果入栈则会破坏栈的单调性,则需要把比入栈元素小的元素全部出栈。单调递减的栈反之。
单调栈的应用:
1.最基础的应用就是给定一组数,针对每个数,寻找它和它右边第一个比它大的数之间有多少个数。
2.给定一序列,寻找某一子序列,使得子序列中的最小值乘以子序列的长度最大。
3.给定一序列,寻找某一子序列,使得子序列中的最小值乘以子序列所有元素和最大。
例题:
1.Bad Hair Day
Some of Farmer John's N cows (1 ≤ N ≤ 80,000) are having a bad hair day! Since each cow is self-conscious about her messy hairstyle, FJ wants to count the number of other cows that can see the top of other cows' heads.
Each cow i has a specified height hi (1 ≤ hi ≤ 1,000,000,000) and is standing in a line of cows all facing east (to the right in our diagrams). Therefore, cow i can see the tops of the heads of cows in front of her (namely cows i+1, i+2, and so on), for as long as these cows are strictly shorter than cow i.
Consider this example:
=
= =
= - = Cows facing right -->
= = =
= - = = =
= = = = = =
1 2 3 4 5 6 Cow#1 can see the hairstyle of cows #2, 3, 4
Cow#2 can see no cow's hairstyle
Cow#3 can see the hairstyle of cow #4
Cow#4 can see no cow's hairstyle
Cow#5 can see the hairstyle of cow 6
Cow#6 can see no cows at all!
Let ci denote the number of cows whose hairstyle is visible from cow i; please compute the sum of c1 through cN.For this example, the desired is answer 3 + 0 + 1 + 0 + 1 + 0 = 5.
Input
Line 1: The number of cows, N.
Lines 2..N+1: Line i+1 contains a single integer that is the height of cow i.
Output
Line 1: A single integer that is the sum of c 1 through cN.
Sample Input
6
10
3
7
4
12
2Sample Output
5#include
#include
#include
#include
#include
#include
#include
#include 2.待补充
3.Feel Good