伸展树c++ 实现
原创文章,转载请声明 :chance_yin http://blog.csdn.net/chance_yin/article/details/35553747
一、为什么要有伸展树
根据80-20黄金法则即80%的访问发生在20%的数据上,所以如果我们能够把经常访问的节点推到靠近根节点的位置,那么就可以极大的提高访问速度。
根据这个思路,我们提出了 “ 旋转到根 ” 这一思路,具体的:每次查找、插入、删除一个节点,我们都使用旋转的方法把这个节点旋转到根节点的位置,并且因为旋转操作能够很好的把其他访问路径上的节点向上移动,所以最后这经常访问的20%的数据基本上都处于靠近根节点的位置。
二、普通AVL树的旋转和伸展树的旋转有什么不同?
AVL树的旋转操作目的是缩小左右子树的高度差,它是全局调控即目的是缩小整棵树的高度,不会针对某一个节点做优化(例如将经常访问的节点移动到根的位置或靠近根的位置)
相反,伸展树的旋转操作目的就是把经常访问的节点移动到根的位置,它不会考虑整棵树是否平衡,旋转完成后,伸展树可能成为一个糟糕的单链表,但伸展树保证在此单链表上查找经常访问的20%节点是最快的。
鉴于基本AVL树和伸展树的旋转目的不同,他们的旋转操作也有一定的区别,具体如下:
(下面的旋转操作看不懂可以继续往下看,只要知道他们的旋转操作有区别就好)
1、处理ZIG-ZIG 形式的旋转操作
(1)普通AVL数的旋转操作
(2)伸展树(这步操作是最明显的区别)
2、处理ZIG-ZAG形式的旋转操作
(1)普通AVL树
(2)伸展树(自顶向下)
三、伸展操作 splay
伸展操作又分为“自底向上” 和 “自顶向下” 两种。其中“自底向上” 比较容易想得到,因为想要把深层的访问节点移动到树根,最直接的思路就是从要访问的节点开始向上慢慢的旋转。
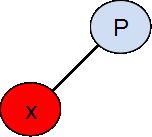
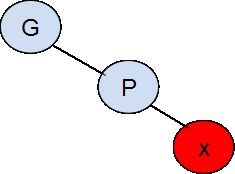
先要给出节点之间的几种连接形式:
注1:
注2:
注3:
1、自底向上伪码
for(;;)
{
if( x 是 P 的左子节点)
{
if( G == NULL ) // zig 形式,见注1(1)
{
x 绕 P 右旋; // 见注4
}
else if( P 是 G 的左子节点 ) // zig-zig 形式见注2(1)
{
P 绕 G 右旋;
x 绕 P 右旋; //见注5
}
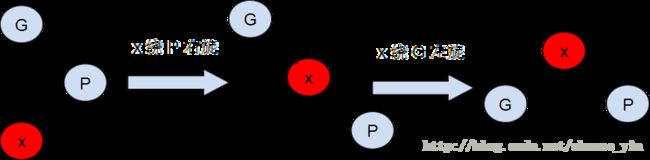
else if( P 是G的右子节点 ) //zig-zag ,形式见注3(1)
{
x 绕 P 右旋;
x 绕 G 左旋; //见注6
}
}
else if( x 是 P 右子节点)
{
“x 是 P 左子节点的镜像操作,和上面的if 操作大同小异,为了减少大家看代码的复杂度,我把它扔到下面的注释中了”
}
}x 是 P 左子节点的镜像操作
else if (x 是 P 右子节点)
{
if( G == NULL) // 见注1(2)
{
x 绕 P 左旋;//见注4(2)
}
else if( P 是 G 右子节点 )//见注2(2)
{
P 绕 G 左旋;
x 绕 P 左旋; //见注5(2)
}
else if( P 是 G 左子节点) //见注3(2)
{
x 绕 P 左旋;
x 绕 G 右旋; //见注6(2)
}
}注4:
(2)镜像:
注5:
(2)
注6:
(1)
(2)
终于把自底向上搞定了.....
自底向上写了半天,但我要说实际使用中,一般都不用这种算法!!
简单分析下不难发现,(1)首先要遍历访问路径上的所有节点,找到要访问的节点x (2)在自底向上调整结构的过程中,必须要记住x 的父节点P和祖父节点G,如果旋转G节点那么还需要记录曾祖父节点GG,如果你不想在struct BinaryNode 节点结构中添加额外的成员来记住父节点,那么就只能使用足够深的栈来记录父节点信息。
所以重点来了,我们使用自顶向下来替代自底向上,在自顶向下算法中,只需要一次遍历访问路径上的节点,并且在访问过程中我们就要完成“旋转到顶的操作”。
2、自顶向下伪码(1)
在自顶向下伪码中,需要再引入两个辅助指针,“左树指针LeftTreeMax” 和 “右树指针RightTreeMin”
从名字应该可以看出这两个指针的作用,LeftTreeMax 始终指向左树中的最右节点,即最左树的最大节点。RightTreeMax 始终指向右树中的最左节点,即最小节点。
分析起来原因有点困难,但如果找出一个特殊情况就比较好看:
先看为什么随着树的深度的加深,能够挂在左树上的节点的值会逐渐变大:
如上图,能挂到左子树上的节点,一定处于访问路径的右分支上,显然随着树的深度的加深,又分支上的节点值越来越大,所以leftTreeMax 永远指向左树上的最大节点。
同理不难分析,为什么RightTreeMin 永远指向右树上的最小值,这里只贴出一张分析图,其他文字分析就不再赘述:
好知道了这些,自顶向下的代码就简单了,具体思路就一句话 “遍历访问路径,在遍历过程中执行适当的旋转和将节点挂载到左右子树上的工作”
for(;;)
{
if(x < G)
{
if(x == G 的左子节点 P ) //zig 形式
{
将G及其右子树挂到右树上;
}
else if( X < G 的左子节点P) // zig-zig
{
P 绕G旋转;
将P和G挂到右树上
}
else (x > G 的左子节点P) //zig-zag
{
将G及其右子树挂到右树上;
将P及其左子数挂到左树上;
}
}
else if(X > G)
{
if(x == G的右子节点P)
{
将G及其左子树挂到左树上;
}
else if( X > G 的右子节点P)
{
将P绕G左旋;
将P和G挂到左树上;
}
else if(X < G右子节点P)
{
将G及其左子树挂到左树上;
将P及其右子树挂到右树上;
}
}
else
break;
}
观察自顶向下的伪代码发现,红色字部分是实际上是相同的语句,重复即罪恶,所以我们可以把他们合并或者说共用同一个语句。特别的zig-zag 形式中的 将"P及其左子树挂到左树上" 这句伪代码是可以丢到镜像 if(X > G) 中去的...... 自己考虑下,如此一来,我们就只剩下两种变换形式“zig(zag)” 和 “zig-zig(zag-zag)” ,而“zig-zag ”可以简化成一个zig和一个zag
for(;;)
{
if( x < G )
{
if(x < G 的左子节点P) //zig-zig
{
P 绕 G 右旋;
}
将当前树的根和根的右子树挂到右树上; //zig
}
else if( x > G )
{
if(x > G 的右子节点P) // zag-zag
{
P 绕 G 左旋;
}
将当前树的根和根的左子树挂到左树上; //zag
}
else
break;
}四、最后再将下具体代码实现(代码来自Mark Allen Weiss 的数据结构与算法分析c++描述)
template
class SplayTree
{
public:
SplayTree()
{
nullnode = new BinaryNode(0,NULL,NULL);
nullnode->left = nullnode->right = nullnode;
root = nullnode; //不赋值为0,则root值是随机数
}
~SplayTree(){};
void insert(const Comparable& x)
{
insert(x,root);
}
void printTree()
{
printTree(root);
}
void splay(const Comparable& x)
{
splay(x,root);
}
private:
typedef struct BinaryNode
{
Comparable element;
struct BinaryNode * left;
struct BinaryNode * right;
BinaryNode(const Comparable& theElement, BinaryNode * lt,BinaryNode * rt):
element(theElement),left(lt),right(rt){};
}BinaryNode;
BinaryNode * root;
BinaryNode * nullnode;
/*
*注释说明:
* T 表示当前的根节点
* p 表示当前根节点的孩子节点
* x 表示待查找元素
* */
void splay(const Comparable& x, BinaryNode *& root)
{
static BinaryNode header(x,nullnode,nullnode);
BinaryNode * leftTreeMax,*rightTreeMin;
header.right = header.left = nullnode; //因为static 语句只会调用一次对象的构造函数,所以必须要在这里清空左右子树
leftTreeMax = rightTreeMin = &header;
nullnode->element = x;
for(;;)
{
if(x < root->element)
{
BinaryNode * leftChild = root->left;
if(x < leftChild->element)
{
rotateWithLeftChild(root); // 该函数执行完成后,root 指向p 节点
}
if(root->left == nullnode) // nullnode 和 这个判断节点为空的语句是否应该在上面的 if(x < leftChild->element) 判断语句之前再放一个的解释见注释7
break;
rightTreeMin->left = root;
rightTreeMin = root;
root = root->left;
}
else if(x > root->element)
{
BinaryNode * rightChild = root->right;
if(x > rightChild->element)
{
rotateWithRightChild(root);
}
if(root->right == nullnode)
break;
leftTreeMax->right = root;
leftTreeMax = root;
root = root->right;
}
else
break;
}
leftTreeMax->right = root->left;
rightTreeMin->left = root->right;
root->left = header.right;
root->right = header.left;
}
/*
* root leftChild
* / / \
* leftChild ==> other root
* / \ /
* left right right
**/
void rotateWithLeftChild(BinaryNode *& root)
{
BinaryNode * leftChild = root->left;
root->left = leftChild->right;
leftChild->right = root;
root = leftChild;
}
/*
* root rightChild
* \ / \
* rightChild root right
* / \ \
* left right left
**/
void rotateWithRightChild(BinaryNode *& root)
{
BinaryNode * rightChild = root->right;
root->right = rightChild->left;
rightChild->left = root;
root = rightChild;
}
void printTree(BinaryNode * node)
{
if(node == nullnode)
{
return;
}
cout << node->element << endl;
printTree(node->left);
printTree(node->right);
}
void remove(const Comparable& x, BinaryNode *& root)
{
BinaryNode * newTree;
//删除一个节点也要重新调整树的结构
//因为伸展树可能极度不平衡,如果使用递归的方法来删除一个
//节点,则在大数据中可能会导致栈溢出
splay(x,root);
if(x == root->element)
{
/*
* 如果左子树为空则右子树的根就是新树的根
* 如果左子树不为空,则使用左子树最大的节点(最右节点)作为新树的根
* */
if(root->left == nullnode)
{
newTree = root->right;
}
else
{
newTree = root->left;
/* 再次重构整个伸展树 */
splay(x,newTree); // 找到左子树最大的节点
newTree->right = root->right; //让左子树最大的节点作为新树的根
}
delete root;
root = newTree;
}
}
void insert(const Comparable& x,BinaryNode *& root)
{
static BinaryNode * newNode = NULL;
if(newNode == NULL)
{
newNode = new BinaryNode(x,nullnode,nullnode);
}
newNode->element = x;
if(root == nullnode)
{
root = newNode;
root->left = root->right = nullnode;
}
else
{
splay(x,root);
if(x < root->element)
{
newNode->left = root->left; //splay 完成后,根据伸展规则root的左子树都小于关键字
newNode->right = root; // root 的右子树都大于关键字,所以要把左子树的元素挂在到
//新节点的左子树上,而root和root的右子树都大于关键字 ,见注释8
root->left = nullnode; //保证所有的空节点都指向nullnode
root = newNode; //新插入的节点作为root节点
}
else if(x > root->element)
{
newNode->right = root->right;
newNode->left = root;
root->right = nullnode;
root = newNode;
}
else
return; // 查到重复元素,则此次new的BinaryNode没有使用,所以下一次插入新的节点时,可以不用重新new
}
newNode = NULL;
}
};
注释7:
1、nullnode 的作用,为什么不用NULL??
(1)分析如果不用nullnode 而是用我们熟悉的NULL来标表示节点为空
那么我们就必须 在 “ if ( x < leftChild->element ) ”判断语句前后都要放一个if(leftChild == NULL)判断,原因是放在“ if ( x < leftChild->element ) ” 之前的if(leftChild == NULL)是为了避免访问空指针的->element元素,即防止出现 NULL->element 的语句的出现。
而之后的if(leftChild == NULL) 是因为 rotateWihtXXXXChild() 语句会改变树的根节点。因为在伸展树中查找一个节点,如果这个节点不存在我们就要返回“访问路径上的最后一个元素”如图:
(2)分析如果我们使用了nullnode,并且规定整棵树中所有空接点全指向nullnode,而不是NULL
那么我们可以在splay 开始时,设置 nullnode == x (要查找的关键字值),这样就可以保证不会出先“NULL->elemetn”空引用的问题,也就省掉了(1)中提到的第一次 if(leftChild == NULL)的判断
最后还要再提一下for(;;)循环出口的问题,如果找到了节点 那么应该从 if(X < root->element ) ....else (X > root->element)....else break; 结构中的break 退出。此时当前结点即要访问的节点; 如果没有找到想访问的节点,则从if(root->leftChild == nullnode) 返回。此时root表示访问路径上最后一个节点。
2、最后一个比较讲究的函数就是 insert 函数了
(1) insert 函数需要保证我们在splay函数中假定的那个前提“整棵树中所有空接点均指向nullnode”
(2)另外insert 开始的static 定义和对于if (newNode == NULL)的判断是考虑了这种情况:如果待插入的节点X 在树中已经存在,则新new 出来的节点可以给下次插入使用。
(3)贴出一张图解释 newNode->left = root->left; :

最后一个图中,蓝色连接表示:newNode->left = root->left; 黄色连接表示:newNode->right = root; 红色连接表示:root->left = nullnode;
五、上面的所有图片就是我能想到的伸展树操作及其实现的所有“难点”了。有错误和不明白的地方欢迎留言交流。