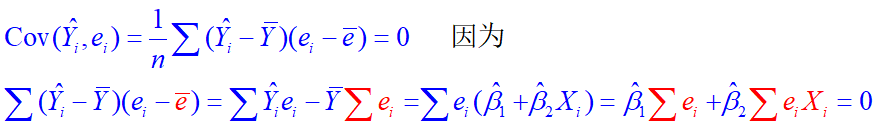- 磨课心得
爬坡启动
这几天,严格的说是一个星期以来,参加中心学校选送县级参赛教师的磨课。参赛课题是人教版小学数学三年级上册分数单元的《认识几分之几》到《分数的简单应用》共五个课题中的一个。今天早上已经抽签定下来,我们乡镇参赛教师抽到的课题是五个参赛课题的第二个课时——《同分母分数大小的比较》,所以这个课题今天下午又给这位参赛老师听了第二遍。通过这几天参与磨课,收获颇多,简要记录于下。一、进一步认同了黄爱华老师所说的“
- 常见Hash算法
LUCIAZZZ
算法哈希算法javaspringboot操作系统spring密码学
部分内容来源:JavaGuide什么是Hash算法哈希算法也叫散列函数或摘要算法,它的作用是对任意长度的数据生成一个固定长度的唯一标识也叫哈希值、散列值或消息摘要哈希算法的是不可逆的,你无法通过哈希之后的值再得到原值哈希值的作用是可以用来验证数据的完整性和一致性哈希算法可以简单分为两类:加密哈希算法:安全性较高的哈希算法,它可以提供一定的数据完整性保护和数据防篡改能力,能够抵御一定的攻击手段,安全
- 成功日记(Day806)
狮子座的兔子姑娘
1、跟l斌约好周一见。2、摘豆角。~0.25h。3、给爸买水泵遥控器。4、和y月简单聊天。~0.25h。5、和谢哥微信闲聊。~0.25h。6、和g夙微信闲唠嗑。~0.5h。7、淘宝协商退掉了买的梨膏糖。~0.25h。8、淘宝买一丢丢吃的。~0.25h。9、帮妈妈串苏子叶。~0.5h。心情:尚可。
- Matlab学习笔记:矩阵基础
MATLAB学习笔记:矩阵基础作为MATLAB的核心,矩阵是处理数据的基础工具。矩阵本质上是一个二维数组,由行和列组成,用于存储和操作数值数据。在本节中,我将详细讲解矩阵的所有知识点,包括创建、索引、运算、函数等,确保内容通俗易懂。我会在关键地方添加MATLAB代码示例,帮助你直观理解。最后,我会总结本课重点,并引出下一节“逻辑基础”的内容。一、什么是矩阵?在MATLAB中,矩阵是一个二维数组,元
- 当深情变成沉默
独善其身_0731
我是一个深情地人,也是一个花心的人,爱过甲乙丙丁,说过海誓山盟。我是一个普通的人,因为我无法给你所有,能给你的不过尔尔,我给你的需要用尽全力,或许只是别人的举手之劳。我脾气不好,不爱表达对你的好,我喜欢默默的去爱一个人,默默的去付出自己所有。我是一个深情的人,我可以为你付出所有,甚至毫无尊严的下跪挽留。可以为了讨你欢心,跟所有人为敌去跟所有人绝交。其实爱一个人我一直都觉得挺简单。只要付出,不断的付
- 【QT常用技术讲解】任务栏图标+socket网络服务+开机自启动
前言首先看网络编程的定义:两个不同主机设备之间的进程通信。C/S(Client-Server)是早期非常典型的软件架构,C/S架构虽然简单,但却非常适用于桌面图形化的QT项目。本篇的QT项目是从真实的项目中简化出来,满足很多相似的场景:创建一个TCP服务,接收到消息后,通过多线程执行后台CMD命令行,并且自动把程序放到系统自启动目录中。覆盖到QT的知识点:任务栏托盘、右键菜单、TCP服务、多线程。
- 2022年京东618红包密令和领取时间和使用时间
一起高省
关于2022淘宝618红包什么时候开始的这个话题,相信小伙伴们是非常有兴趣了解的,因为这个话题是目前网络上非常火热的,既然大家都想要知道的话,下面跟小编一起悄悄,今年活动没任何套路,最高可领22888元了,比往年的618翻了许多倍。2022年618密令红包提前公布‼️宝618密令红包公布!收藏起来!时间:5.29日20点—6.20日每天抽三次红包,最高可领28888r‼️参与方式很简单,直接去桃宝
- 简单WEB登录页面代码实现
逆流的飞鱼
简单代码java
longin.html:登录页面,此处action引用**/**类型的地址,JSP可以用${pageContext.request.contextPath}/LS用户名:密码:LoginServlet.java用户和前台WEB页面数据进行交互packageit.tongyou.web.servlet;importjava.io.IOException;importjava.io.PrintWrit
- 拉姆达表达式(Lambda Expressions)
xwdpepsi
C#.netlambdaclass编译器
让我们先看一个简单的拉姆达表达式:x=>x/2这个表达式的意思是:x为参数,对x进行相应的操作后的结果作为返回值。通过这个拉姆达表达式,我们可以看到:这个表达式没有任何类型信息,但这并不代表拉姆达表达式是和类型无关的。在实际运用上,编译器会根据表达式的上下文判断上述x的类型及返回值的类型。例如:usingSystem;usingSystem.Linq;publicclassLambdaTest{s
- 第十五章 Caché 变量大全 $STORAGE 变量
Cache技术分享
第十五章Caché变量大全$STORAGE变量包含可用于局部变量存储的字节数。大纲$STORAGE$S描述$STORAGE返回可用于当前进程分区中的本地变量存储的字节数。$STORAGE的初始值由$ZSTORAGE的值确定,该值是该进程可用的最大内存量。$ZSTORAGE值(以千字节为单位)越大,$STORAGE值(以字节为单位)越大。但是,$ZSTORAGE和$STORAGE之间的关系不是简单的
- 【MoodVine】DeepSeek聊天持久化(2):Spring AI + Redis实现对话记忆管理
一只鱼吖
【西瓜和晚霞】MoodVinespringredisjava
在上一篇文章中,我们介绍了如何引入SpringAI,本文将深入探讨如何实现聊天记录的持久化存储。一、初始方案:内存存储的局限性在项目初期,我们使用简单的内存存储实现聊天记录管理:创建ChatController@RestController@RequestMapping("/chat")publicclassChatController{privatefinalOllamaChatModeloll
- 十大广告赚钱平台APP排行榜:一天收益50元天花板软件曝光
清风导师
十大广告赚钱平台APP排行榜,实测2024年看广告一天50元收益是真的还是骗局?最近小编发现很多赚钱副业项目开始返璞归真,简单说就是随着管理的越来越严格,现在一些新模式或者特别火爆的玩法会比较低调,反而是老玩法旧瓶装新酒优化升级了许多,比如广告赚钱类型,很多人过去印象并不好,不过现在甚至有些软件可以做到日赚50+的利润,确实是另外眼前一亮。广告赚钱日赚50+是真的吗?实事求是的评级,在过去几年广告
- redis-plus-plus安装与使用
Yu_Lijing
redis数据库缓存
目录一.安装hiredis二.接口三.使用四.总结C++操作redis的库有很多.咱们使用redis-plus-plus.这个库的功能强大,使用简单.Github地址:https://github.com/sewenew/redis-plus-plus一.安装hiredisredis-plus-plus是基于hiredis实现的.hiredis是一个C语言实现的redis客户端.因此需要先安装hi
- 《财务自由之路》2
拥有俩娃的少女妈
图片发自App二、责任意味着什么1、你并非要对所有的事情负责,但你总是要在个人范畴内对自己对时间的判断和反映负责,这听起来简单,但做起来很不容易。并不是发生在我们身上的事情让我们痛苦,而是我们对待事情的反应。2、责任的意思就是有技巧地进行回应。你把责任给了谁,也就给了他权力。你要问自己,我们想要自己掌控将来事态的发展,还是让我们的错误以及其后果掌握将来的事态?3、拓宽你的可控领域A、可控领域,指的
- 10分钟搞定 MinIO 单节点多磁盘部署!打造稳定高可用对象存储【二】
MinIO是一个**高性能、开源的对象存储系统**,主要用于存储非结构化数据(如图片、视频、文档、备份等),与AmazonS3完全兼容。它被广泛用于云原生应用、大数据分析、AI模型存储、容器平台(如Kubernetes)等场景。MinIO支持多种部署模式,其中:单节点单磁盘(Single-NodeSingle-Drive)模式适用于开发测试、小规模应用或资源受限的场景。它的部署简单,不依赖集群、分
- 亲子日记25
我死行了吧
2018年10月13日.星期六.晴今天我和两个孩子都休息,我们三睡到9点多才起床,起来吃了点东西,姐姐开始写作业,先把周四晚上的作业补上,告诉她要写拼音,她说老师说从第一页开始写,我说,那你写吧,一会的功夫说写完了,从a写到了ui……,孩,你倒是省事,怎么简单怎么来……图片发自App我告诉她老师不是布置这个作业,她立马垮了脸,可怜兮兮的说,我已经写了很多了啊,怎么还有那么多!?我说,是啊,你为了偷
- STM32F4-ETH通信(lwip)——学习笔记_stm32 lwip
2401_84010497
程序员嵌入式
7、CSMA/CD冲突检测:8、MAC子层:MAC数据包、MAC数据包格式、MAC地址:MAC地址由48位数字组成,它是网卡的物理地址,在以太网传输的最底层,就是根据MAC地址来收发数据的。部分MAC地址用于广播和多播,在同一个网络里不能有两个相同的MAC地址。PC的网卡在出厂时已经设置好了MAC地址,但也可以通过一些软件来进行修改,在嵌入式的以太网控制器中可由程序进行配置。数据包中的DA是目标地
- 机器学习数据预处理阶段为什么需要——归一化处理
参考:https://www.cnblogs.com/bjwu/p/8977141.html通常,在DataScience中,预处理数据有一个很关键的步骤就是数据的标准化。这里主要引用sklearn文档中的一些东西来说明,主要把各个标准化方法的应用场景以及优缺点总结概括,以来充当笔记。提升模型精度在机器学习算法的目标函数(例如SVM的RBF内核或线性模型的l1和l2正则化),许多学习算法中目标函数
- 使用CrewAI创建一个研究团队
AI量化投资
php开发语言多智能体智能体人工智能
本指导文档将带你一步步完成使用CrewAI框架创建你的第一个AI代理团队的过程。通过这个简单的示例,你将学习如何构建一个研究团队,用于研究和分析指定主题,并生成一份综合报告。本教程基于CrewAI官方文档,适合初学者快速上手。前提条件在开始之前,请确保你已完成以下准备工作:安装Python:确保你的系统安装了Python版本在3.10到3.13之间。你可以通过以下命令检查Python版本:pyth
- 消息队列MQ
不辉放弃
kafka大数据开发数据库
消息队列(MessageQueue,简称MQ)是一种基于异步通信模式的中间件技术,核心作用是在分布式系统中实现消息的存储、传递和缓冲,解决不同组件/服务之间的通信耦合问题,提升系统的灵活性、可靠性和可扩展性。一、核心概念与本质消息队列的本质是一个“存储消息的容器”,但它并非简单的存储工具,而是通过一套规则(如消息路由、持久化、确认机制等)实现“生产者”和“消费者”的解耦通信:生产者(Produce
- 三个人的友情,我选择退出
蓝空的空
这是我在微博上看到的,三个女孩的故事:女孩A挽着女孩B的胳膊和女孩B说着手机里的内容,而女孩C在旁边显得很多余。女孩A突然看见前面很热闹,二话不说就拉着女孩B跑过去,而第三个女孩看着她们跑过去的背影,默默转身,离开。看着很简单的动作,却挑明了一个很简单的事实:三个人的友情,我只能退出。小学时,我,潇潇,桂桂是能玩到一起的朋友。无论做什么事,都会在一起。初中时,我们还是在一所学校,因为学校离家远,所
- “重复”定义函数的睿智(Python/与ai助手“智普清言”深度交流)
梦幻精灵_cq
笔记学习
镜像双胞谬重复,定制便捷巧活工。 笔记模板由python脚本于2025-07-1612:16:30创建,本篇笔记适合至少通晓一门语言,熟悉基本编程范式的coder翻阅。学习的细节是欢悦的历程 博客的核心价值:在于输出思考与经验,而不仅仅是知识的简单复述。Python官网: 这里,才python前沿。英文原版,原汁原味,才是寻根溯源的正统。地址:https://www.python.org/F
- 偶拾《退让》,一阙仿七律带出的文化思考(中文诗创作)
梦幻精灵_cq
笔记学习
礼貌温言沐春风,谦让理解通彼此。 笔记模板由python脚本于2025-07-0111:29:03创建,本篇笔记适合喜欢中文仿古七言诗的coder翻阅。学习的细节是欢悦的历程 博客的核心价值:在于输出思考与经验,而不仅仅是知识的简单复述。Python官网: 这里,才python前沿。英文原版,原汁原味,才是寻根溯源的正统。地址:https://www.python.org/Free: 大咖
- 最简单的赚钱方法是什么?盘点5个简单快速赚钱方法
优惠券高省
在家可以做什么赚钱?很多宝妈、上班族、大学生可能经常会有这种困惑。他们大多有空闲时间,但不想出去全职或兼职,想在家赚钱。今天分享五种在家赚钱的方法。第一:互联网淘宝客选择全网佣金最高的「高省」APP,高省邀请码:110000。分享商品及推广APP做团队赚钱,适合新手小白(有导师一对一带)日入500+。自用省钱,分享赚钱,高省含有自动云发单功能,可以解放双手,自动发群发圈赚钱。使用【高省app】网购
- 2022.04.18简单日记
谢谋淦
2022.04.18晴不冷不热早饭牛奶袋豆浆茶叶蛋菜包花费6.5块钱。来客户买U盘收费100块钱128gb。进货399+69.9+840+71块钱。午饭买两个馒头花费1.5块钱加鱼汤。睡午觉。醒了去买20块钱瓜子带去办公室人员吃,送了发票去等着结账。骑电动车出去爬山。股市收盘三大指数涨跌不一,个股涨一片,我的股票海默科技跌6.46%,收盘价格4.92块钱,华仁药业跌1.21%,收盘价格4.08块钱
- 2021-09-12
姗姗_52f9
《对来访者对咨询师真的重要起来》刘姗姗中原焦点团队坚持分享第1504天第167次咨询约练观察员不管是心理咨询还是心理治疗,终究是围绕“人”进行工作的,与来访者建立良好的关系,不是简单几句空话就能成立的,咨询师需要展现出人情味,真正地与来访者站在一起。一个懂很多技术的咨询师,并不一定能切实地帮到来访者。如果咨询师永远与对面的人保持距离,能够完全地隔离自己的情绪感受,不受来访者的分毫影响,我觉得这不叫
- 金蝶云苍穹树形单据体创建及插件的简单使用
涎涎
树形单据体介绍单据体,用来在界面上显示、录入多行多列数据。树形单据体与单据体的不同之处在于,树形单据体中的数据行之间,可以设置父子从属关系,形成树形结构。树形单据体创建通过模板创建单据带组织模板单据选中单据体添加高级面板选中高级面板子容器,插入树形单据体按如下步骤设置工具栏设置树形单据体表名t_treebill_entry树形单据体功能添加字段开启显示序号列和显示选择列保存并授权退出当前账号,ad
- 菠萝这么做,美味不上火
一米财富NO1
现在是吃菠萝的季节,菠萝很美味,相信我们大家都吃过,特别是孩子都喜欢吃菠萝,但是很多朋友都会说吃了菠萝上火。今天听朋友说这样做菠萝,孩子爱吃还不上火,就试做了一次,很简单,也很好吃,分享给大家,希望大家喜欢。菠萝一个,去皮,清洗干净,切成小片,锅里加点水,把菠萝放进去,水没过菠萝就好,中火先烧开转小火煮大约5分钟,再加点冰糖,小火再煮大约十分钟左右关火,放凉就可以吃了,酸酸甜甜真好吃。冰糖可以根据
- kafka--基础知识点--5.4--max.in.flight.requests.per.connection
一、参数定义max.in.flight.requests.per.connection是Kafka生产者客户端配置参数,用于控制生产者与单个Broker连接中未确认请求的最大数量。简单来说,它限制了生产者在等待之前发送的消息确认(ACK)时,可以同时向同一个Broker发送的未完成请求数量。二、核心作用吞吐量与延迟的平衡:高值(如5):允许生产者并行发送多个请求,提高吞吐量,但可能增加延迟(因需要
- 祭,我们的十年!
Voyageur晨
回忆,不是为了感伤,而是想更好的祭奠我们的青春!匆匆十年,或为了梦想,或为了生计,大家天各一方,这唯一能关联的一个地方,也许就只有家乡!十年前,初中毕业的我们,没有饭店KTV,简简单单在我家、你家、或者他家,十来人动手,一桌丰盛的餐食也就完成。席间,一包辣条还未传到我手,就已是空袋子,相互间就这辣条的调侃,也是最美味的下饭菜!饭后小广场的篮球场,被我们这群半大不小的学生霸占,就连那杀马特的非主流小
- 辗转相处求最大公约数
沐刃青蛟
C++漏洞
无言面对”江东父老“了,接触编程一年了,今天发现还不会辗转相除法求最大公约数。惭愧惭愧!
为此,总结一下以方便日后忘了好查找。
1.输入要比较的两个数a,b
忽略:2.比较大小(因为后面要的是大的数对小的数做%操作)
3.辗转相除(用循环不停的取余,如a%b,直至b=0)
4.最后的a为两数的最大公约数
&
- F5负载均衡会话保持技术及原理技术白皮书
bijian1013
F5负载均衡
一.什么是会话保持? 在大多数电子商务的应用系统或者需要进行用户身份认证的在线系统中,一个客户与服务器经常经过好几次的交互过程才能完成一笔交易或者是一个请求的完成。由于这几次交互过程是密切相关的,服务器在进行这些交互过程的某一个交互步骤时,往往需要了解上一次交互过程的处理结果,或者上几步的交互过程结果,服务器进行下
- Object.equals方法:重载还是覆盖
Cwind
javagenericsoverrideoverload
本文译自StackOverflow上对此问题的讨论。
原问题链接
在阅读Joshua Bloch的《Effective Java(第二版)》第8条“覆盖equals时请遵守通用约定”时对如下论述有疑问:
“不要将equals声明中的Object对象替换为其他的类型。程序员编写出下面这样的equals方法并不鲜见,这会使程序员花上数个小时都搞不清它为什么不能正常工作:”
pu
- 初始线程
15700786134
暑假学习的第一课是讲线程,任务是是界面上的一条线运动起来。
既然是在界面上,那必定得先有一个界面,所以第一步就是,自己的类继承JAVA中的JFrame,在新建的类中写一个界面,代码如下:
public class ShapeFr
- Linux的tcpdump
被触发
tcpdump
用简单的话来定义tcpdump,就是:dump the traffic on a network,根据使用者的定义对网络上的数据包进行截获的包分析工具。 tcpdump可以将网络中传送的数据包的“头”完全截获下来提供分析。它支 持针对网络层、协议、主机、网络或端口的过滤,并提供and、or、not等逻辑语句来帮助你去掉无用的信息。
实用命令实例
默认启动
tcpdump
普通情况下,直
- 安卓程序listview优化后还是卡顿
肆无忌惮_
ListView
最近用eclipse开发一个安卓app,listview使用baseadapter,里面有一个ImageView和两个TextView。使用了Holder内部类进行优化了还是很卡顿。后来发现是图片资源的问题。把一张分辨率高的图片放在了drawable-mdpi文件夹下,当我在每个item中显示,他都要进行缩放,导致很卡顿。解决办法是把这个高分辨率图片放到drawable-xxhdpi下。
&nb
- 扩展easyUI tab控件,添加加载遮罩效果
知了ing
jquery
(function () {
$.extend($.fn.tabs.methods, {
//显示遮罩
loading: function (jq, msg) {
return jq.each(function () {
var panel = $(this).tabs(&
- gradle上传jar到nexus
矮蛋蛋
gradle
原文地址:
https://docs.gradle.org/current/userguide/maven_plugin.html
configurations {
deployerJars
}
dependencies {
deployerJars "org.apache.maven.wagon
- 千万条数据外网导入数据库的解决方案。
alleni123
sqlmysql
从某网上爬了数千万的数据,存在文本中。
然后要导入mysql数据库。
悲剧的是数据库和我存数据的服务器不在一个内网里面。。
ping了一下, 19ms的延迟。
于是下面的代码是没用的。
ps = con.prepareStatement(sql);
ps.setString(1, info.getYear())............;
ps.exec
- JAVA IO InputStreamReader和OutputStreamReader
百合不是茶
JAVA.io操作 字符流
这是第三篇关于java.io的文章了,从开始对io的不了解-->熟悉--->模糊,是这几天来对文件操作中最大的感受,本来自己认为的熟悉了的,刚刚在回想起前面学的好像又不是很清晰了,模糊对我现在或许是最好的鼓励 我会更加的去学 加油!:
JAVA的API提供了另外一种数据保存途径,使用字符流来保存的,字符流只能保存字符形式的流
字节流和字符的难点:a,怎么将读到的数据
- MO、MT解读
bijian1013
GSM
MO= Mobile originate,上行,即用户上发给SP的信息。MT= Mobile Terminate,下行,即SP端下发给用户的信息;
上行:mo提交短信到短信中心下行:mt短信中心向特定的用户转发短信,你的短信是这样的,你所提交的短信,投递的地址是短信中心。短信中心收到你的短信后,存储转发,转发的时候就会根据你填写的接收方号码寻找路由,下发。在彩信领域是一样的道理。下行业务:由SP
- 五个JavaScript基础问题
bijian1013
JavaScriptcallapplythisHoisting
下面是五个关于前端相关的基础问题,但却很能体现JavaScript的基本功底。
问题1:Scope作用范围
考虑下面的代码:
(function() {
var a = b = 5;
})();
console.log(b);
什么会被打印在控制台上?
回答:
上面的代码会打印 5。
&nbs
- 【Thrift二】Thrift Hello World
bit1129
Hello world
本篇,不考虑细节问题和为什么,先照葫芦画瓢写一个Thrift版本的Hello World,了解Thrift RPC服务开发的基本流程
1. 在Intellij中创建一个Maven模块,加入对Thrift的依赖,同时还要加上slf4j依赖,如果不加slf4j依赖,在后面启动Thrift Server时会报错
<dependency>
- 【Avro一】Avro入门
bit1129
入门
本文的目的主要是总结下基于Avro Schema代码生成,然后进行序列化和反序列化开发的基本流程。需要指出的是,Avro并不要求一定得根据Schema文件生成代码,这对于动态类型语言很有用。
1. 添加Maven依赖
<?xml version="1.0" encoding="UTF-8"?>
<proj
- 安装nginx+ngx_lua支持WAF防护功能
ronin47
需要的软件:LuaJIT-2.0.0.tar.gz nginx-1.4.4.tar.gz &nb
- java-5.查找最小的K个元素-使用最大堆
bylijinnan
java
import java.util.Arrays;
import java.util.Random;
public class MinKElement {
/**
* 5.最小的K个元素
* I would like to use MaxHeap.
* using QuickSort is also OK
*/
public static void
- TCP的TIME-WAIT
bylijinnan
socket
原文连接:
http://vincent.bernat.im/en/blog/2014-tcp-time-wait-state-linux.html
以下为对原文的阅读笔记
说明:
主动关闭的一方称为local end,被动关闭的一方称为remote end
本地IP、本地端口、远端IP、远端端口这一“四元组”称为quadruplet,也称为socket
1、TIME_WA
- jquery ajax 序列化表单
coder_xpf
Jquery ajax 序列化
checkbox 如果不设定值,默认选中值为on;设定值之后,选中则为设定的值
<input type="checkbox" name="favor" id="favor" checked="checked"/>
$("#favor&quo
- Apache集群乱码和最高并发控制
cuisuqiang
apachetomcat并发集群乱码
都知道如果使用Http访问,那么在Connector中增加URIEncoding即可,其实使用AJP时也一样,增加useBodyEncodingForURI和URIEncoding即可。
最大连接数也是一样的,增加maxThreads属性即可,如下,配置如下:
<Connector maxThreads="300" port="8019" prot
- websocket
dalan_123
websocket
一、低延迟的客户端-服务器 和 服务器-客户端的连接
很多时候所谓的http的请求、响应的模式,都是客户端加载一个网页,直到用户在进行下一次点击的时候,什么都不会发生。并且所有的http的通信都是客户端控制的,这时候就需要用户的互动或定期轮训的,以便从服务器端加载新的数据。
通常采用的技术比如推送和comet(使用http长连接、无需安装浏览器安装插件的两种方式:基于ajax的长
- 菜鸟分析网络执法官
dcj3sjt126com
网络
最近在论坛上看到很多贴子在讨论网络执法官的问题。菜鸟我正好知道这回事情.人道"人之患好为人师" 手里忍不住,就写点东西吧. 我也很忙.又没有MM,又没有MONEY....晕倒有点跑题.
OK,闲话少说,切如正题. 要了解网络执法官的原理. 就要先了解局域网的通信的原理.
前面我们看到了.在以太网上传输的都是具有以太网头的数据包.
- Android相对布局属性全集
dcj3sjt126com
android
RelativeLayout布局android:layout_marginTop="25dip" //顶部距离android:gravity="left" //空间布局位置android:layout_marginLeft="15dip //距离左边距
// 相对于给定ID控件android:layout_above 将该控件的底部置于给定ID的
- Tomcat内存设置详解
eksliang
jvmtomcattomcat内存设置
Java内存溢出详解
一、常见的Java内存溢出有以下三种:
1. java.lang.OutOfMemoryError: Java heap space ----JVM Heap(堆)溢出JVM在启动的时候会自动设置JVM Heap的值,其初始空间(即-Xms)是物理内存的1/64,最大空间(-Xmx)不可超过物理内存。
可以利用JVM提
- Java6 JVM参数选项
greatwqs
javaHotSpotjvmjvm参数JVM Options
Java 6 JVM参数选项大全(中文版)
作者:Ken Wu
Email:
[email protected]
转载本文档请注明原文链接 http://kenwublog.com/docs/java6-jvm-options-chinese-edition.htm!
本文是基于最新的SUN官方文档Java SE 6 Hotspot VM Opt
- weblogic创建JMC
i5land
weblogicjms
进入 weblogic控制太
1.创建持久化存储
--Services--Persistant Stores--new--Create FileStores--name随便起--target默认--Directory写入在本机建立的文件夹的路径--ok
2.创建JMS服务器
--Services--Messaging--JMS Servers--new--name随便起--Pers
- 基于 DHT 网络的磁力链接和BT种子的搜索引擎架构
justjavac
DHT
上周开发了一个磁力链接和 BT 种子的搜索引擎 {Magnet & Torrent},本文简单介绍一下主要的系统功能和用到的技术。
系统包括几个独立的部分:
使用 Python 的 Scrapy 框架开发的网络爬虫,用来爬取磁力链接和种子;
使用 PHP CI 框架开发的简易网站;
搜索引擎目前直接使用的 MySQL,将来可以考虑使
- sql添加、删除表中的列
macroli
sql
添加没有默认值:alter table Test add BazaarType char(1)
有默认值的添加列:alter table Test add BazaarType char(1) default(0)
删除没有默认值的列:alter table Test drop COLUMN BazaarType
删除有默认值的列:先删除约束(默认值)alter table Test DRO
- PHP中二维数组的排序方法
abc123456789cba
排序二维数组PHP
<?php/*** @package BugFree* @version $Id: FunctionsMain.inc.php,v 1.32 2005/09/24 11:38:37 wwccss Exp $*** Sort an two-dimension array by some level
- hive优化之------控制hive任务中的map数和reduce数
superlxw1234
hivehive优化
一、 控制hive任务中的map数: 1. 通常情况下,作业会通过input的目录产生一个或者多个map任务。 主要的决定因素有: input的文件总个数,input的文件大小,集群设置的文件块大小(目前为128M, 可在hive中通过set dfs.block.size;命令查看到,该参数不能自定义修改);2.
- Spring Boot 1.2.4 发布
wiselyman
spring boot
Spring Boot 1.2.4已于6.4日发布,repo.spring.io and Maven Central可以下载(推荐使用maven或者gradle构建下载)。
这是一个维护版本,包含了一些修复small number of fixes,建议所有的用户升级。
Spring Boot 1.3的第一个里程碑版本将在几天后发布,包含许多