现代控制理论4——线性系统状态方程的解

注：本文是在MOOC平台上学习西北工业大学《现代控制理论基础》（郭建国、赵斌、郭宗易）的课程进行随笔记录与整理

一.线性定常连续系统状态方程的解——齐次方程

1.求解

齐次状态方程：x`=Ax

其解描述的是：
即无控情况下在初始状态作用下系统的自由运动

解法：
将标量齐次微分方程的解法推广到向量中
标量中：
标量微分方程： x`=ax
解为： x(t)=e^at · x(0)

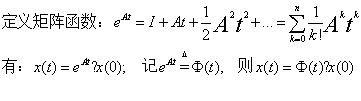
向量中：
法一：幂级数法（设齐次状态方程的解是t的向量幂级数）

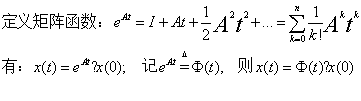
其中e^At，又称为矩阵指数函数/状态转移矩阵
（问号处并没有东西…）
法二：拉氏变化法

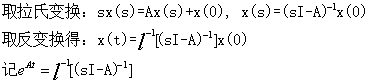
可以发现，两种方法的结果是相同互通的
注：无论A是否奇异，是否可逆，矩阵（sI-A）的逆都存在

2.状态转移矩阵的性质

（1）Ф(0)=1
有：x(t)=Ф(t)x(0),
得：x(0)=Ф(0)x(0)=x(0)
即：零时刻为初始状态

（2）Ф`(t)=AФ(t)=Ф(t)A

求A的时候可以用Ф(0)的导数来求，即：
Ф`(0)=A

（3）Ф(t1 +/- t2)
=Ф(t1) Ф(+/- t2)
=Ф(+/- t2) Ф(t1)

（4)
Ф(t)的逆矩阵 =Ф(-t)
Ф(-t)的逆矩阵 =Ф(t)
（证明：Ф(t-t)=Ф(t)Ф(-t)=Ф(0)=I）

（5)
x(t) = Ф(t-t0) x(t0)
首先有：x(t0) = Ф(t0) x(0)

（6）时间分段：
Ф(t2-t0) = Ф(t2-t1) Ф(t1-t0)

（7）k个相乘变为可加
【Ф(t)】^k = Ф(kt)

(8)当AB=BA时，有：
e^(A-B)t = e^At ×e^Bt = e^Bt × e^At

（9）状态转移矩阵引入非奇异线性变换后：

二.线性定常连续系统状态方程的解——非齐次方程

非齐次的解，是在初始状态和控制输入共同作用下系统的运动；或有控状态下系统的受迫运动

1.求解

（1）积分法
思路：两边同乘e^-At
解为：

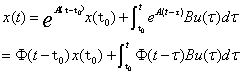
解的第一项是对初始状态的相应分量，第二项是对控制输入的相应分量
（由于：输入为0，只有第一项；初值为0即x0为0，只有第二项）

（2）拉氏变换法
sx(s)= Ax(s) + x(0) + Bu(s)
(sI-A) x(s) = x(0) + Bu(s)
整理后，取反拉式变化后，会得到两个函数先相乘后反拉式变化的情况，此时需要应用卷积定理
最后处理可得，与积分法有相同的结果

三.传函矩阵

1.由动态方程求传函矩阵

在初始条件为0时，对动态方程
x`=Ax+Bu, y=Cx+Du
取拉氏变换：
可得到：

G（s）（q×p）为系统传函矩阵，表示初始条件为0时，输入向量与输出向量拉氏变换式之间的传递关系

而对于单输入单输出系统，G（s）则是传递函数。此时若G（s）为对角方阵，则q=p
此时系统为解耦系统，整个系统由q§个独立系统组成

2.闭环系统中的传函矩阵

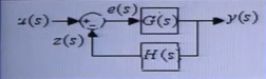
u：输入 e：偏差 z：反馈 y：输出
G：前向通路传递矩阵 H：反馈通路传递矩阵
开环：
z = Hy = HGe （注意HG不能写反）
HG为开环传递矩阵，确定偏差向量反馈向量间的传递关系

闭环：
y = Ge = G(u-z) = Gu-GHy
y=(I+GH)^(-1) · Gu
记Ф为闭环传递矩阵，Ф=(I+GH)^(-1) · G

e = u-z = u-HGe
e=(I+HG)^(-1)·u
记Фe为误差传递矩阵,Фe=(I+HG)^(-1)
它确定输入向量至偏差向量间的传递关系

四.线性离散系统的动态方程及其解

离散：假设采样等间隔，间隔内变量保持常值

对多输入多输出系统有：
x(k+1) = Gx(k) + Hu(k)
y(k) = Cx(k) + Du(k)

还可以通过对定常连续动态方程进行离散化
令t0=kT,有x(t0) = x(kT) = x(k);
令t=(k+1)T,有x[(k+1)T] = x(k+1)

定常离散动态方程的解：
令k=0,1,…k-1，可得到T,2T…kT