【计算机视觉】图像内容分类

---

一、K邻近分类法（KNN）

（一）KNN概述

KNN算法是机器学习里面比较简单的一个分类算法。它通过测量不同特征值之间的距离来进行分类。

KNN算法的思想：对于任意n维输入向量，分别对应于特征空间中的一个点，输出为该特征向量所对应的类别标签或预测值。

KNN算法的工作原理：KNN是通过测量不同特征值之间的距离（一般使用欧氏距离或曼哈顿距离）进行分类。它的思路是：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别，其中K通常是不大于20的整数。KNN算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。

如下图，绿色圆要被决定赋予哪个类，是红色三角形还是蓝色四方形？如果K=3，由于红色三角形所占比例为2/3，绿色圆将被赋予红色三角形那个类，如果K=5，由于蓝色四方形比例为3/5，因此绿色圆被赋予蓝色四方形类。

说明了KNN算法的结果很大程度取决于K的选择。

（二）KNN步骤

1、准备样本数据集（样本中每个数据都已经分好类，并具有分类标签）；
2、使用样本数据进行训练；
3、输入测试数据A；
4、计算A与样本集的每一个数据之间的距离；
5、按照距离递增次序排序；
6、选取与A距离最小的k个点；
7、计算前k个点所在类别的出现频率；
8、返回前k个点出现频率最高的类别作为A的预测分类。

（三）实验过程（包含代码）

1、创建两个不同的二维点集，一个用来训练，一个用来测试。

from numpy.random import randn
import pickle
from pylab import *

#创建二维样本数据
n = 100
# 两个正态分布数据集
class_1 = 0.9 * randn(n,2)
class_2 = 1.8 * randn(n,2) + array([5,1])
labels = hstack((ones(n),-ones(n)))

# 用Pickle模块保存
with open('points_normal.pkl', 'wb') as f:
    pickle.dump(class_1,f)
    pickle.dump(class_2,f)
    pickle.dump(labels,f)

print ("save OK!")

#正态分布，并使数据成环绕状分布
class_1 = 0.2 * randn(n,2)
r = 0.5 * randn(n,1) + 5
angle = 2*pi * randn(n,1)
class_2 = hstack((r*cos(angle),r*sin(angle)))
labels = hstack((ones(n),-ones(n)))

# 用Pickle保存
with open('points_ring.pkl', 'wb') as f:
    pickle.dump(class_1,f)
    pickle.dump(class_2,f)
    pickle.dump(labels,f)
    
print ("save OK!")

#得到4个二维数据集文件，每个分布都有两个文件，一个用来训练，另一个用来测试

注意：因为要得到两个数据集，所以应该用不同的保存文件名运行该脚本两次。

此时文件夹生成数据集为

2、使用KNN分类器对数据进行分类

# 使用KNN分类器
import pickle
from pylab import *
from PCV.classifiers import knn
from PCV.tools import imtools

pklist=['points_normal.pkl','points_ring.pkl']

figure()

# 用Pickle载入二维数据点
for i, pklfile in enumerate(pklist):
    with open(pklfile, 'rb') as f:
        class_1 = pickle.load(f)
        class_2 = pickle.load(f)
        labels = pickle.load(f)

    with open(pklfile[:-4]+'_test.pkl', 'rb') as f:
        class_1 = pickle.load(f)
        class_2 = pickle.load(f)
        labels = pickle.load(f)

    model = knn.KnnClassifier(labels,vstack((class_1,class_2))) 
    #用Pickle模块创建了一个KNN分类器模型

    # 在测试数据集的第一个数据点上进行测试
    print (model.classify(class_1[0]))

#可视化所有测试数据点的分类
    #定义绘图函数
    def classify(x,y,model=model):
        return array([model.classify([xx,yy]) for (xx,yy) in zip(x,y)])

    # 绘制分类边界
    subplot(1,2,i+1)
    imtools.plot_2D_boundary([-6,6,-6,6],[class_1,class_2],classify,[1,-1])
    titlename=pklfile[:-4]
    title(titlename)
show()

运行得最终的分类情况如下：

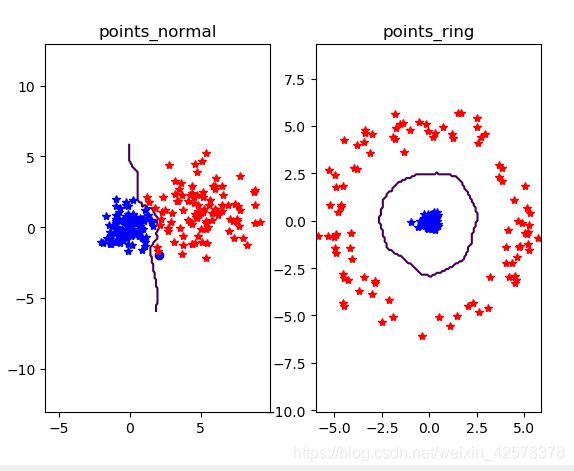
在运行的结果图中，蓝色数据密集些，红色数据比较分散，但是KNN分类器还是能够将两类数据很好地进行分类。

---

二、用稠密SIFT作为图像特征（dense sift）

在一幅图像上应用稠密SIFT描述子的例子（代码）

需要先添加一些额外的参数（放在dsift.py文件中）来得到稠密SIFT特征

dsift.py文件如下：

from PIL import Image
from numpy import *
import os

from PCV.localdescriptors import sift


def process_image_dsift(imagename,resultname,size=20,steps=10,force_orientation=False,resize=None):

    im = Image.open(imagename).convert('L')
    if resize!=None:
        im = im.resize(resize)
    m,n = im.size
    
    if imagename[-3:] != 'pgm':
        #create a pgm file
        im.save('tmp.pgm')
        imagename = 'tmp.pgm'

    # create frames and save to temporary file
    scale = size/3.0
    x,y = meshgrid(range(steps,m,steps),range(steps,n,steps))
    xx,yy = x.flatten(),y.flatten()
    frame = array([xx,yy,scale*ones(xx.shape[0]),zeros(xx.shape[0])])
    savetxt('tmp.frame',frame.T,fmt='%03.3f')
    
    path = os.path.abspath(os.path.join(os.path.dirname("__file__"),os.path.pardir))
    path = path + "\\ch08\\win32vlfeat\\sift.exe "
    if force_orientation:
        cmmd = str(path+imagename+" --output="+resultname+
                    " --read-frames=tmp.frame --orientations")
    else:
        cmmd = str(path+imagename+" --output="+resultname+
                    " --read-frames=tmp.frame")
    os.system(cmmd)
    print ('processed', imagename, 'to', resultname)

主要代码如下：

from PCV.localdescriptors import sift, dsift
from pylab import  *
from PIL import Image

dsift.process_image_dsift('empire.jpg','empire.dsift',70,30,True)
l,d = sift.read_features_from_file('empire.dsift')
im = array(Image.open('empire.jpg'))
sift.plot_features(im,l,True)
title('dense SIFT')
show()

运行结果为：

---

三、图像分类：手势识别（实验过程代码）

进行手势的图像分类中，采用稠密SIFT描述子来表示这些手势图像，并且建立一个简单的手势识别系统。此处使用的手势下载自静态手势数据库，将下载后的所有图像放在一个名为uniform的文件夹中，每一类均分两组，并分别放入名为train和test的两个文件夹中。

实现过程：
1、获得每幅图像的稠密SIFT特征，并且对每一幅图像创建一个特征文件.dsift：

for i, im in enumerate(imlist):
    print (im)
    dsift.process_image_dsift(im,im[:-3]+'dsift',90,40,True)
    l,d = sift.read_features_from_file(im[:-3]+'dsift')

结果如下：

2、绘制出带有描述子的这些手势的图像并显示：

    dirpath, filename=os.path.split(im)
    im = array(Image.open(im))
    #显示手势含义title
    titlename=filename[:-14]
    subplot(2,3,i+1)
    sift.plot_features(im,l,True)
    title(titlename)
show()

结果如下：

3、定义一个辅助函数，用于从文件中读取SIFT描述子：

def read_gesture_features_labels(path):

    featlist = [os.path.join(path,f) for f in os.listdir(path) if f.endswith('.dsift')]
    features = []
    for featfile in featlist:
        l,d = sift.read_features_from_file(featfile)
        features.append(d.flatten())
    features = array(features)

    labels = [featfile.split('/')[-1][0] for featfile in featlist]
    return features,array(labels)

4、读取训练集、测试集的特征和标记信息：

features,labels = read_gesture_features_labels('gesture/train/')
test_features,test_labels = read_gesture_features_labels('gesture/test/')
classnames = unique(labels)

5、测试KNN并且算出准确率：

k = 1
knn_classifier = knn.KnnClassifier(labels,features)
res = array([knn_classifier.classify(test_features[i],k) for i in
range(len(test_labels))])
# accuracy
acc = sum(1.0*(res==test_labels)) / len(test_labels)
print ('Accuracy:', acc)

6、打印标记和相应的混淆矩阵：

def print_confusion(res,labels,classnames):
    n = len(classnames)
    # confusion matrix
    class_ind = dict([(classnames[i],i) for i in range(n)])
    confuse = zeros((n,n))
    for i in range(len(test_labels)):
        confuse[class_ind[res[i]],class_ind[test_labels[i]]] += 1
    print ('Confusion matrix for')
    print (classnames)
    print (confuse)

print_confusion(res,test_labels,classnames)

结果如下：

这说明该例子中有81%的图像是正确的。