Python计算机视觉编程 - LeNet卷积模型实现Mnist手写体训练
摘要
1.看mnist数据库特点
2.LeNet-5原理
3.数值化结果
1.mnist数据库特点
MNIST数据集是一个手写数字数据集,每一张图片都是0到9中的单个数字。
MNIST数据库的来源是两个数据库的混合,一个来自Census Bureau employees(SD-3),一个来自high-school students(SD-1);有训练样本60000个,测试样本10000个。训练样本和测试样本中,employee和student写的都是各占一半。60000个训练样本一共大概250个人写的。训练样本和测试样本的来源人群没有交集。MNIST数据库也保留了手写数字与身份的对应关系。我们可以使用Tensorflow提供的input_data.py 脚本来加载数据集。
2.LeNet-5原理
2.1、简介
卷积神经网络是一种特殊的多层神经网络,像其它的神经网络一样,卷积神经网络也使用一种反向传播算法来进行训练,不同之处在于网络的结构。卷积神经网络的网络连接具有局部连接、参数共享的特点。局部连接是相对于普通神经网络的全连接而言的,是指这一层的某个节点只与上一层的部分节点相连。参数共享是指一层中多个节点的连接共享相同的一组参数。
LeNet-5正是卷积神经网络的一种。

2.2原理简述
LeNet一共有7层(不包括输入层)
输入层:
输入图像的大小为3232,这要比mnist数据库中的最大字母(2828)还大。
作用: 图像较大,这样做的目的是希望潜在的明显特征,比如笔画断续,角点等能够出现在最高层特征监测子感受野的中心。
其他层:
C1,C3,C5为卷积层,S2,S4为降采样层,F6为全连接层,还有一个输出层。
每一个层都有多个Feature Map(每个Feature Map中含有多个神经元),输入通过一种过滤器作用,提取输入的一种特征,得到一个不同的Feature Map。如下图所示:
2.3、各层详解
卷积运算的优点:通过卷积运算,可以使原信号特征增强,并且降低噪声。
卷积对于二维图像中的效果就是:对于图像中的每个像素邻域求加权和得到该像素点的输出值。

-
C1卷积层
● C1 是一个卷积层,由6个Feature Map组成。 每一个Feature Map中的每个神经元与输入中55的区域相连(也就是Filter的大小),Feature Map的大小为2828,
● C1一共有156个参数,因为55个参数加上一个bias,一共又有6个Filter,所以为:(55+1)6=156,一共有156(28*28) = 122304个连接。 -
S2 下采样层(Pooling)
下采样的作用: 利用图像的局部相关性原理,对图像进行子抽样,可以减少数据处理量,同时又保留有用的信息。
同样的,有61414, 6个Feature Map。
池化层一般有两种方式:
● (1) Max_Pooling: 选择Pooling窗口中最大值最为采样值
● (2) Mean_Pooling: 将Pooling窗口中的所有值相加取平均,然后以平均值最为采样值。
说明:
每个单元的22的感受野()并不重叠,因此S2中每一个Feature Map的大小为C1中Feature Map中大小的1/4。行列各位1/2。所以,S2有12个可训练的参数和5880个连接。个人感觉,5880是这么来的,Filter的大小为:22,一个偏差bias,6个Feature Map,则可训练参数个数为:(22+1)6 = 30,连接数为:30(1414)= 5880
12 则为: 6个2*2的小方块,加上一个bias,为(1+1)*6=12卷积过程中,用一个可训练的过滤器fx去卷积一个输入图像,然后添加一个偏置bx ,得到卷积层Cx 。子采样过程就是:每个邻域4个像素变为一个像素,然后加上标量Wx 加权,最后再增加偏置bx+1 ,接着通过一个sigmoid激活函数,产生一个大概缩小了4倍的特征映射图Sx+1。
-
C3层 卷积层
同样的,Filter大小认为55,去卷积S2,得到的Feature Map为1010大小。每一个Feature Map中包含1010个神经元。C3层有16个不同的Filter,所以会得到16个不同的Feature Map。
C3中的每一个Feature Map连接到S2的所有6个Feature Map或者是几个Feature Map。表示本层的Feature Map是上一层提取的Feature Map的不同组合。为什么不把S2的每一个Feature Map连接到S3的每一个Feature Map中?原因有2: 第一,不完全连接机制连接的数量保持在合理范围,第二,这样破坏了网络的对称性,由于不同的Feature Map有不同的输入,所以迫使他们抽取不同的特征(理想状态特征互补)。
如果:C3的前6个Feature Map以S2中的3个相邻的Feature Map子集为输入,接下来的6个Feature Map以S2中相邻的4个Feature Map作为输入,接下来的3个以不相邻的4个Feature Map子集作为输入,最后一个将S2中所有的Feature Map作为输入的话,C3将会有1516个可训练参数和151600个连接。
因为6(325+1) + 6(425+1) + 3(425+1) + 1(625+1) = 1516。连接数为:15161010=151600。 -
S4层 Pooling层
由16个55的Feature Map组成,Feature Map中每个单元与C3中相应的Feature Map的22邻域相连。
S4有32个可训练的参数和2000个连接
同S2,(1+1)16=32. 连接数为: (22+1) 16 * 55 = 2000 -
C5 卷积层
这一层有120个Feature Map,每个单元与S4层的全部的16个55的邻域相连。 S4的Feature Map的大小也是55,这一层的Filter大小也是55,所以,C5的Feature Map的大小为11。此时构成了S4与C5之间的全连接。但这里C5表示为卷积层而不是全连接层,是因为如果LeNet的输入变大,而其他保持不变,此时的Feature Map的大小就比11要大。
C5有48120个可训练的链接: (55*16 +1) *120 = 48120。 -
F6 全连接层
有84个单元(之所以是84是因为输入层的设计),F6计算输入向量和权重向量之间的点积,再加上一个偏置,最后将其传递给sigmoid函数产生一个单元i的一个状态。
一共有10164个可训练的连接,为:84*(120+1)=10164。 -
输出层
输出层由欧式径向基函数(Euclidean Radial Basis Function)单元组成,每类一个单元,每个单元有84个输入。
也就是说: 每个输入RBF单元计算输入向量和参数向量之间的欧氏距离。输入离参数向量越远,RBF输出越大。一个RBF输出可以理解为衡量输入模式和RBF相关联的一个模型的匹配程度的惩罚项。给定一个输入模式,损失函数应该能使F6的配置和RBF参数向量(模式的期望分类)足够接近。
每一个单元的参数是人工选取并保持固定的。这些参数向量的成分被设计成-1或1。虽然这些参数可以以-1或1等概论方式任取,或者是构成一个纠错码,但是被设计成一个相应字符类的7*12的格式化图片。
网络的训练过程为:
分为四步:
(1) 在一批数据中取样(Sample a batch of data)
(2)前向过程计算得到损失(Forward prop it through the graph, get loss)
(3)反向传播计算梯度(Backprop to calculate the gradient)
(4)利用梯度进行梯度的更新(Updata the parameters using the gradient)
这里,网络的训练主要分为2个大的阶段:
1)从样本集中取一个样本(X,Yp),将X输入网络;
2)计算相应的实际输出Op。
在此阶段,信息从输入层经过逐级的变换,传送到输出层。这个过程也是网络在完成训练后正常运行时执行的过程。在此过程中,网络执行的是计算(实际上就是输入与每层的权值矩阵相点乘,得到最后的输出结果):
Op=Fn(…(F2(F1(XpW(1))W(2))…)W(n))
第二阶段,向后传播阶段
1)算实际输出Op与相应的理想输出Yp的差;
2)按极小化误差的方法反向传播调整权矩阵。
原理参照:https://blog.csdn.net/Sakura55/article/details/81393827
3.数值化结果
环境:python3.6+TensorFlow(GPU)
TensorFlow安装导引:https://blog.csdn.net/titansm/article/details/88755173
3.1读取package训练集进行训练
代码:
import tensorflow as tf
import numpy as np # 习惯加上这句,但这边没有用到
from tensorflow.examples.tutorials.mnist import input_data
import matplotlib.pyplot as plt
mnist = input_data.read_data_sets('MNIST_data/', one_hot=True)
sess = tf.InteractiveSession()
# 1、权重初始化,偏置初始化
# 为了创建这个模型,我们需要创建大量的权重和偏置项
# 为了不在建立模型的时候反复操作,定义两个函数用于初始化
def weight_variable(shape):
initial = tf.truncated_normal(shape,stddev=0.1)#正太分布的标准差设为0.1
return tf.Variable(initial)
def bias_variable(shape):
initial = tf.constant(0.1,shape=shape)
return tf.Variable(initial)
# 2、卷积层和池化层也是接下来要重复使用的,因此也为它们定义创建函数
# tf.nn.conv2d是Tensorflow中的二维卷积函数,参数x是输入,w是卷积的参数
# strides代表卷积模块移动的步长,都是1代表会不遗漏地划过图片的每一个点,padding代表边界的处理方式
# padding = 'SAME',表示padding后卷积的图与原图尺寸一致,激活函数relu()
# tf.nn.max_pool是Tensorflow中的最大池化函数,这里使用2 * 2 的最大池化,即将2 * 2 的像素降为1 * 1的像素
# 最大池化会保留原像素块中灰度值最高的那一个像素,即保留最显著的特征,因为希望整体缩小图片尺寸
# ksize:池化窗口的大小,取一个四维向量,一般是[1,height,width,1]
# 因为我们不想再batch和channel上做池化,一般也是[1,stride,stride,1]
def conv2d(x, w):
return tf.nn.conv2d(x, w, strides=[1,1,1,1],padding='SAME') # 保证输出和输入是同样大小
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1,2,2,1], strides=[1,2,2,1],padding='SAME')
# 3、参数
# 这里的x,y_并不是特定的值,它们只是一个占位符,可以在TensorFlow运行某一计算时根据该占位符输入具体的值
# 输入图片x是一个2维的浮点数张量,这里分配给它的shape为[None, 784],784是一张展平的MNIST图片的维度
# None 表示其值的大小不定,在这里作为第1个维度值,用以指代batch的大小,means x 的数量不定
# 输出类别y_也是一个2维张量,其中每一行为一个10维的one_hot向量,用于代表某一MNIST图片的类别
x = tf.placeholder(tf.float32, [None,784], name="x-input")
y_ = tf.placeholder(tf.float32,[None,10]) # 10列
# 4、第一层卷积,它由一个卷积接一个max pooling完成
# 张量形状[5,5,1,32]代表卷积核尺寸为5 * 5,1个颜色通道,32个通道数目
w_conv1 = weight_variable([5,5,1,32])
b_conv1 = bias_variable([32]) # 每个输出通道都有一个对应的偏置量
# 我们把x变成一个4d 向量其第2、第3维对应图片的宽、高,最后一维代表图片的颜色通道数(灰度图的通道数为1,如果是RGB彩色图,则为3)
x_image = tf.reshape(x,[-1,28,28,1])
# 因为只有一个颜色通道,故最终尺寸为[-1,28,28,1],前面的-1代表样本数量不固定,最后的1代表颜色通道数量
h_conv1 = tf.nn.relu(conv2d(x_image, w_conv1) + b_conv1) # 使用conv2d函数进行卷积操作,非线性处理
h_pool1 = max_pool_2x2(h_conv1) # 对卷积的输出结果进行池化操作
# 5、第二个和第一个一样,是为了构建一个更深的网络,把几个类似的堆叠起来
# 第二层中,每个5 * 5 的卷积核会得到64个特征
w_conv2 = weight_variable([5,5,32,64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, w_conv2) + b_conv2)# 输入的是第一层池化的结果
h_pool2 = max_pool_2x2(h_conv2)
# 6、密集连接层
# 图片尺寸减小到7 * 7,加入一个有1024个神经元的全连接层,
# 把池化层输出的张量reshape(此函数可以重新调整矩阵的行、列、维数)成一些向量,加上偏置,然后对其使用Relu激活函数
w_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1,7 * 7 * 64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, w_fc1) + b_fc1)
# 7、使用dropout,防止过度拟合
# dropout是在神经网络里面使用的方法,以此来防止过拟合
# 用一个placeholder来代表一个神经元的输出
# tf.nn.dropout操作除了可以屏蔽神经元的输出外,
# 还会自动处理神经元输出值的scale,所以用dropout的时候可以不用考虑scale
keep_prob = tf.placeholder(tf.float32, name="keep_prob")# placeholder是占位符
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)
# 8、输出层,最后添加一个softmax层
w_fc2 = weight_variable([1024,10])
b_fc2 = bias_variable([10])
y_conv = tf.nn.softmax(tf.matmul(h_fc1_drop, w_fc2) + b_fc2, name="y-pred")
# 9、训练和评估模型
# 损失函数是目标类别和预测类别之间的交叉熵
# 参数keep_prob控制dropout比例,然后每100次迭代输出一次日志
cross_entropy = tf.reduce_sum(-tf.reduce_sum(y_ * tf.log(y_conv),reduction_indices=[1]))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
# 预测结果与真实值的一致性,这里产生的是一个bool型的向量
correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
# 将bool型转换成float型,然后求平均值,即正确的比例
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# 初始化所有变量,在2017年3月2号以后,用 tf.global_variables_initializer()替代tf.initialize_all_variables()
sess.run(tf.initialize_all_variables())
# 保存最后一个模型
saver = tf.train.Saver(max_to_keep=1)
for i in range(1000):
batch = mnist.train.next_batch(64)
if i % 100 == 0:
train_accuracy = accuracy.eval(feed_dict={x: batch[0], y_: batch[1],keep_prob: 1.0})
print("Step %d ,training accuracy %g" % (i, train_accuracy))
train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})
print("test accuracy %f " % accuracy.eval(feed_dict={x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0}))
# 保存模型于文件夹
saver.save(sess,"save/model")
3.2读取Images训练集进行训练
代码:
#coding:utf8
import os
import cv2
import numpy as np
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
sess = tf.InteractiveSession()
def getTrain():
train=[[],[]] # 指定训练集的格式,一维为输入数据,一维为其标签
# 读取所有训练图像,作为训练集
train_root="mnist_train"
labels = os.listdir(train_root)
for label in labels:
imgpaths = os.listdir(os.path.join(train_root,label))
for imgname in imgpaths:
img = cv2.imread(os.path.join(train_root,label,imgname),0)
array = np.array(img).flatten() # 将二维图像平铺为一维图像
array=MaxMinNormalization(array)
train[0].append(array)
label_ = [0,0,0,0,0,0,0,0,0,0]
label_[int(label)] = 1
train[1].append(label_)
train = shuff(train)
return train
def getTest():
test=[[],[]] # 指定训练集的格式,一维为输入数据,一维为其标签
# 读取所有训练图像,作为训练集
test_root="mnist_test"
labels = os.listdir(test_root)
for label in labels:
imgpaths = os.listdir(os.path.join(test_root,label))
for imgname in imgpaths:
img = cv2.imread(os.path.join(test_root,label,imgname),0)
array = np.array(img).flatten() # 将二维图像平铺为一维图像
array=MaxMinNormalization(array)
test[0].append(array)
label_ = [0,0,0,0,0,0,0,0,0,0]
label_[int(label)] = 1
test[1].append(label_)
test = shuff(test)
return test[0],test[1]
def shuff(data):
temp=[]
for i in range(len(data[0])):
temp.append([data[0][i],data[1][i]])
import random
random.shuffle(temp)
data=[[],[]]
for tt in temp:
data[0].append(tt[0])
data[1].append(tt[1])
return data
count = 0
def getBatchNum(batch_size,maxNum):
global count
if count ==0:
count=count+batch_size
return 0,min(batch_size,maxNum)
else:
temp = count
count=count+batch_size
if min(count,maxNum)==maxNum:
count=0
return getBatchNum(batch_size,maxNum)
return temp,min(count,maxNum)
def MaxMinNormalization(x):
x = (x - np.min(x)) / (np.max(x) - np.min(x))
return x
# 1、权重初始化,偏置初始化
# 为了创建这个模型,我们需要创建大量的权重和偏置项
# 为了不在建立模型的时候反复操作,定义两个函数用于初始化
def weight_variable(shape):
initial = tf.truncated_normal(shape,stddev=0.1)#正太分布的标准差设为0.1
return tf.Variable(initial)
def bias_variable(shape):
initial = tf.constant(0.1,shape=shape)
return tf.Variable(initial)
# 2、卷积层和池化层也是接下来要重复使用的,因此也为它们定义创建函数
# tf.nn.conv2d是Tensorflow中的二维卷积函数,参数x是输入,w是卷积的参数
# strides代表卷积模块移动的步长,都是1代表会不遗漏地划过图片的每一个点,padding代表边界的处理方式
# padding = 'SAME',表示padding后卷积的图与原图尺寸一致,激活函数relu()
# tf.nn.max_pool是Tensorflow中的最大池化函数,这里使用2 * 2 的最大池化,即将2 * 2 的像素降为1 * 1的像素
# 最大池化会保留原像素块中灰度值最高的那一个像素,即保留最显著的特征,因为希望整体缩小图片尺寸
# ksize:池化窗口的大小,取一个四维向量,一般是[1,height,width,1]
# 因为我们不想再batch和channel上做池化,一般也是[1,stride,stride,1]
def conv2d(x, w):
return tf.nn.conv2d(x, w, strides=[1,1,1,1],padding='SAME') # 保证输出和输入是同样大小
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1,2,2,1], strides=[1,2,2,1],padding='SAME')
iterNum = 10
batch_size=1024
print("load train dataset.")
train=getTrain()
print("load test dataset.")
test0,test1=getTest()
# 3、参数
# 这里的x,y_并不是特定的值,它们只是一个占位符,可以在TensorFlow运行某一计算时根据该占位符输入具体的值
# 输入图片x是一个2维的浮点数张量,这里分配给它的shape为[None, 784],784是一张展平的MNIST图片的维度
# None 表示其值的大小不定,在这里作为第1个维度值,用以指代batch的大小,means x 的数量不定
# 输出类别y_也是一个2维张量,其中每一行为一个10维的one_hot向量,用于代表某一MNIST图片的类别
x = tf.placeholder(tf.float32, [None,784], name="x-input")
y_ = tf.placeholder(tf.float32,[None,10]) # 10列
# 4、第一层卷积,它由一个卷积接一个max pooling完成
# 张量形状[5,5,1,32]代表卷积核尺寸为5 * 5,1个颜色通道,32个通道数目
w_conv1 = weight_variable([5,5,1,32])
b_conv1 = bias_variable([32]) # 每个输出通道都有一个对应的偏置量
# 我们把x变成一个4d 向量其第2、第3维对应图片的宽、高,最后一维代表图片的颜色通道数(灰度图的通道数为1,如果是RGB彩色图,则为3)
x_image = tf.reshape(x,[-1,28,28,1])
# 因为只有一个颜色通道,故最终尺寸为[-1,28,28,1],前面的-1代表样本数量不固定,最后的1代表颜色通道数量
h_conv1 = tf.nn.relu(conv2d(x_image, w_conv1) + b_conv1) # 使用conv2d函数进行卷积操作,非线性处理
h_pool1 = max_pool_2x2(h_conv1) # 对卷积的输出结果进行池化操作
# 5、第二个和第一个一样,是为了构建一个更深的网络,把几个类似的堆叠起来
# 第二层中,每个5 * 5 的卷积核会得到64个特征
w_conv2 = weight_variable([5,5,32,64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, w_conv2) + b_conv2)# 输入的是第一层池化的结果
h_pool2 = max_pool_2x2(h_conv2)
# 6、密集连接层
# 图片尺寸减小到7 * 7,加入一个有1024个神经元的全连接层,
# 把池化层输出的张量reshape(此函数可以重新调整矩阵的行、列、维数)成一些向量,加上偏置,然后对其使用Relu激活函数
w_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1,7 * 7 * 64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, w_fc1) + b_fc1)
# 7、使用dropout,防止过度拟合
# dropout是在神经网络里面使用的方法,以此来防止过拟合
# 用一个placeholder来代表一个神经元的输出
# tf.nn.dropout操作除了可以屏蔽神经元的输出外,
# 还会自动处理神经元输出值的scale,所以用dropout的时候可以不用考虑scale
keep_prob = tf.placeholder(tf.float32, name="keep_prob")# placeholder是占位符
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)
# 8、输出层,最后添加一个softmax层
w_fc2 = weight_variable([1024,10])
b_fc2 = bias_variable([10])
y_conv = tf.nn.softmax(tf.matmul(h_fc1_drop, w_fc2) + b_fc2, name="y-pred")
# 9、训练和评估模型
# 损失函数是目标类别和预测类别之间的交叉熵
# 参数keep_prob控制dropout比例,然后每100次迭代输出一次日志
cross_entropy = tf.reduce_sum(-tf.reduce_sum(y_ * tf.log(y_conv),reduction_indices=[1]))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
# 预测结果与真实值的一致性,这里产生的是一个bool型的向量
correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
# 将bool型转换成float型,然后求平均值,即正确的比例
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# 初始化所有变量,在2017年3月2号以后,用 tf.global_variables_initializer()替代tf.initialize_all_variables()
sess.run(tf.initialize_all_variables())
# 保存最后一个模型
saver = tf.train.Saver(max_to_keep=1)
for i in range(iterNum):
for j in range(int(len(train[1])/batch_size)):
imagesNum=getBatchNum(batch_size,len(train[1]))
batch = [train[0][imagesNum[0]:imagesNum[1]],train[1][imagesNum[0]:imagesNum[1]]]
train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})
if i % 2 == 0:
train_accuracy = accuracy.eval(feed_dict={x: batch[0], y_: batch[1],keep_prob: 1.0})
print("Step %d ,training accuracy %g" % (i, train_accuracy))
print("test accuracy %f " % accuracy.eval(feed_dict={x: test0, y_:test1, keep_prob: 1.0}))
# 保存模型于文件夹
saver.save(sess,"save/model")
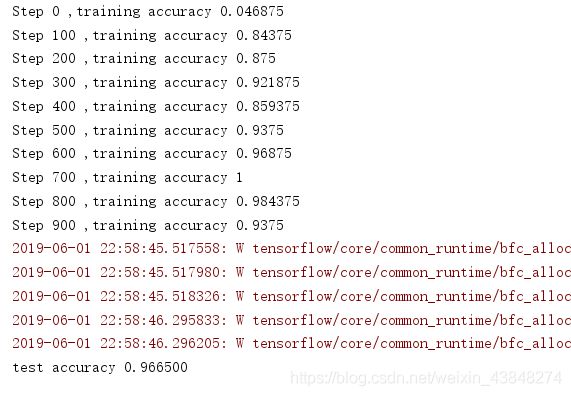
结果:


仅仅只允许到Step8便提示内存耗尽报错中止。根据其他同道的情况,了解到使用GPU运行此代码皆会报错。而使用CPU运行则要消耗大约一个小时的时间。CPU运行处的结果和3.1相近,精确度皆超过了90%
3.3手写体数字识别
代码:
import tensorflow as tf
import numpy as np
import tkinter as tk
from tkinter import filedialog
from PIL import Image, ImageTk
from tkinter import filedialog
import time
def creat_windows():
win = tk.Tk() # 创建窗口
sw = win.winfo_screenwidth()
sh = win.winfo_screenheight()
ww, wh = 400, 450
x, y = (sw-ww)/2, (sh-wh)/2
win.geometry("%dx%d+%d+%d"%(ww, wh, x, y-40)) # 居中放置窗口
win.title('手写体识别') # 窗口命名
bg1_open = Image.open("timg.jpg").resize((300, 300))
bg1 = ImageTk.PhotoImage(bg1_open)
canvas = tk.Label(win, image=bg1)
canvas.pack()
var = tk.StringVar() # 创建变量文字
var.set('')
tk.Label(win, textvariable=var, bg='#C1FFC1', font=('宋体', 21), width=20, height=2).pack()
tk.Button(win, text='选择图片', width=20, height=2, bg='#FF8C00', command=lambda:main(var, canvas), font=('圆体', 10)).pack()
win.mainloop()
def main(var, canvas):
file_path = filedialog.askopenfilename()
bg1_open = Image.open(file_path).resize((28, 28))
pic = np.array(bg1_open).reshape(784,)
bg1_resize = bg1_open.resize((300, 300))
bg1 = ImageTk.PhotoImage(bg1_resize)
canvas.configure(image=bg1)
canvas.image = bg1
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
saver = tf.train.import_meta_graph('save/model.meta') # 载入模型结构
saver.restore(sess, 'save/model') # 载入模型参数
graph = tf.get_default_graph() # 加载计算图
x = graph.get_tensor_by_name("x-input:0") # 从模型中读取占位符变量
keep_prob = graph.get_tensor_by_name("keep_prob:0")
y_conv = graph.get_tensor_by_name("y-pred:0") # 关键的一句 从模型中读取占位符变量
prediction = tf.argmax(y_conv, 1)
predint = prediction.eval(feed_dict={x: [pic], keep_prob: 1.0}, session=sess) # feed_dict输入数据给placeholder占位符
answer = str(predint[0])
var.set("预测的结果是:" + answer)
if __name__ == "__main__":
creat_windows()
结果:
正确结果:

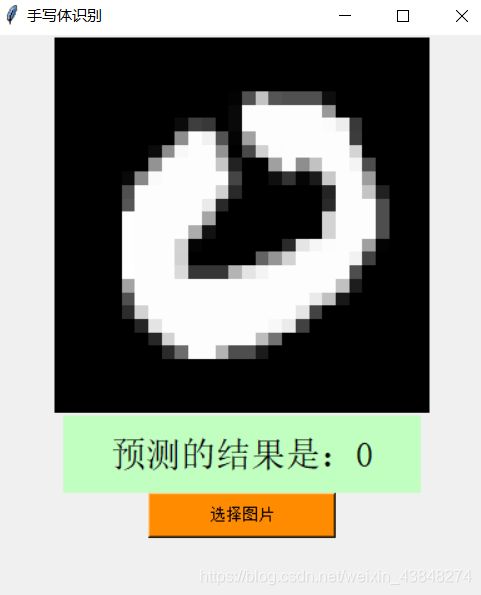
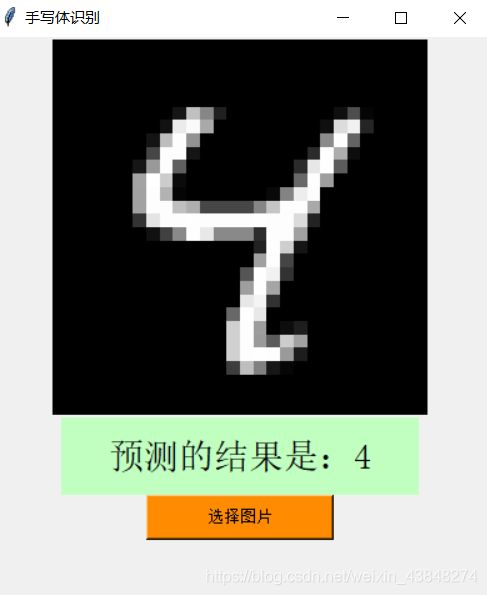

错误结果:

可以看到,除了最后一图将4识别为了6之外,其余图片均识别正确。由此,可以简单认定,在除却图像较为扭曲或模棱两可的情况下,Mnist手写体的识别能力基本得以保证,在图片特征较为明显的情况下更可以保证绝大部分情况下的正确识别。