【论文笔记】Crowd Counting Using Scale-Aware Attention Networks
文章目录
- Abstract
- 1. Introduction
- 2. Related Work
- 3. Our Approach
- 3.1. Multi-Scale Feature Extractor
- 3.2. Global Scale Attention
- 3.3. Local Scale Attention
- 3.4. Fusion Network
- 3.5. Loss Function
- 4. Experiments
Abstract
人群计数的一大挑战是图像的尺度不同。这篇文章提出了一种创新的scale-aware attention网络来处理尺度问题。最近的深度学习架构中流行使用注意力机制,我们的模型可以自动关注图像的某些全局和局部scale。通过结合全局和局部的sacle attention,我们的模型在几个经典数据集上优于其他方法。
1. Introduction
对于任意给定的人群图像,我们的目标是估计输入图像的密度图,其中密度图中的每个像素值对应于输入图像相应位置的人群密度。最后对密度图求和或积分得到最终的人群数。
crowd counting有很多现实生活的应用,例如监视,公共安全,交通监控,城市规划等。人群计数的方法也可以应用于其他领域的计数,例如对显微图像中的细胞或细菌进行计数[28],对动物进行生态研究[1],对交通控制中的车辆进行计数。
人群计数的挑战是多方面的,包括严重的遮挡,透视变形,人群密度的变化等等,如图1所示。早期的人群计数工作是基于人头检测的方法,近几年来,CNNs在人群计数领域越来越普遍,大多数基于CNN的方法通过预测图像的密度图来获得人群数,人群计数的准确度很大程度依赖于生成密度图的质量。

近几年来,attention机制在不同的计算机视觉任务中取得了很不错的效果。注意机制不是从整个图像中提取特征,而是使模型根据需要专注于最相关的特征。在本文中,我们使用类似的想法,开发了具有scale-aware attention的CNN架构,用于人群密度的估算和计数。
这篇文章的贡献如下:
- 在基于CNN的人群计数方法中使用了attention机制。
- 其次,先前的工作通常使用注意力模型来关注图像中的某些空间位置。在我们的工作中,我们是将注意力集中在某些scale上。
2. Related Work
3. Our Approach
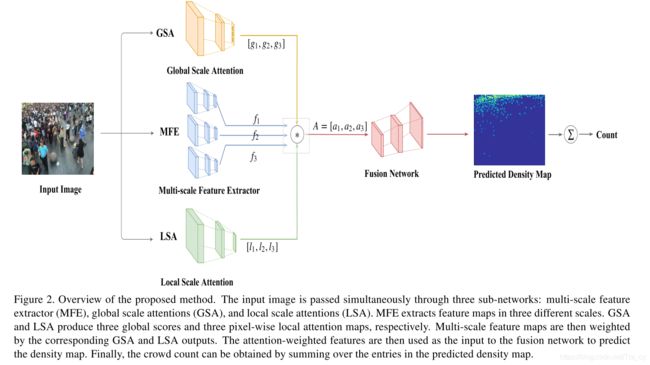
人群密度在不同图像之间以及同一图像内的不同空间位置上都可能发生巨大变化。我们建议同时使用全局和局部注意力权重来捕获人群密度的图像间和图像内变化。这使我们的模型能够以适当的比例自适应地使用要素。如图2所示,我们的模型包含几个模块:multi-scale feature extractor (MFE), global scale attentions (GSA), local scale attention (LSA), and the fusion network (FN)。接下来,我们详细描述这几个模块。
3.1. Multi-Scale Feature Extractor
这个模块的作用是从输入图片中提取多尺度的特征图。我们使用类似多分支结构来获取多尺度特征图,如图3所示。
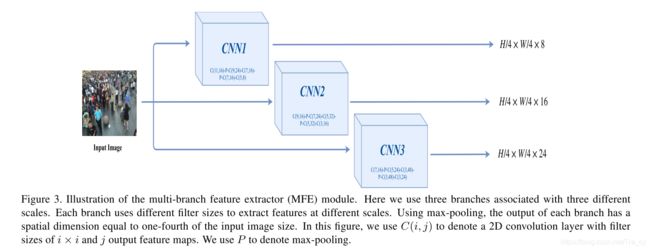
它以任意图片大小作为输入,每个分支独立处理输入图片,每个分支由具有不同滤波器大小的卷积层的多个块组成。通过在这些分支中选择不同的过滤器大小,我们可以更改每个分支中的接收场并以不同的比例捕获特征。每个分支还具有几个最大池化层。我们在最大池化层中选择filter大小,以便每个分支中的输出特征图的空间尺寸等于输入图像尺寸的四分之一。
3.2. Global Scale Attention
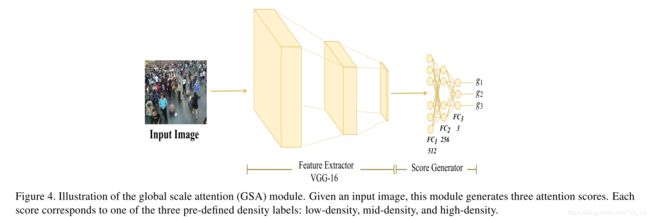
在我们的模型中,我们使用Global Scale Attention(GSA)模块来捕获有关图像密度的全局上下文信息。该模块获取输入图像并产生三个注意力得分,每个得分对应于三个预定义的密度标签级别之一:低密度,中密度和高密度。密度级别的数量等于多尺度特征提取模块中的尺度数量(第3.1节)。 GSA的架构如图4所示。
对于每张图片,GSA都输出三个分数 g i ( i = 1 , 2 , 3 ) g_i (i=1,2,3) gi(i=1,2,3),代表输入图像属于三个密度标签中的每个的程度。在pipeline的末尾使用softmax层将分数(可以解释为“注意”)归一化以求和为1。
3.3. Local Scale Attention
GSA模块捕获图像的整体density level。但是一张图片在不同的区域具有不同的density map。全局density level不足以捕获图像中不同位置的局部上下文信息。我们加入了local scale attention(LSA)模块来捕获一张图片不同区域的局部尺度信息。LSA生成代表不同位置上的比例尺信息的逐点注意图。与全球关注模块类似,在这里我们还考虑了三个不同的scale level。与产生三个标量得分的GSA不同,LSA会产生三个逐像素的attention map。这些注意图具有与相应的多尺度特征图相同的空间尺寸(第3.1节)。
LSA模块包括8个卷积层和两个最大池化层,接着是3个全连接层,如图5所示。在模块的末端放置一个sigmoid层,以确保attention map中的值在0到1之间。

3.4. Fusion Network
融合网络为输入图片产生最终的密度图。该模块从图像中提取提取的特征图,然后通过全局和局部注意力分数对特征图进行加权。输出预测密度图,然后求和得到人群总数。

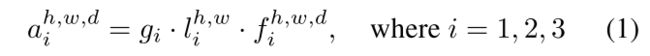
三个scale特征图的尺度都是 H / 4 ∗ W / 4 H/4 * W/4 H/4∗W/4, H ∗ W H*W H∗W是输入图像的大小,但是,特征图在不同scale之间可以具有不同的深度(即通道数)。在这里,低密度,中密度和高密度的通道数分别设置为24、16和8。然后将不同比例的注意权重特征图concat在一起,并输入到融合网络(FN)模块中以生成密度图。FN模块由几个卷积层以及2个反卷积层组成,后者将要素图的大小调整为H / 2×W / 2,最后调整为H×W,其中H×W是原始输入图像的空间尺寸。该阶段的输出是尺寸为H×W×16的特征图。最后,我们用1*1的卷积产生一个通道为1,大小为 H ∗ W H*W H∗W的密度图DM,最后求和得到人数。
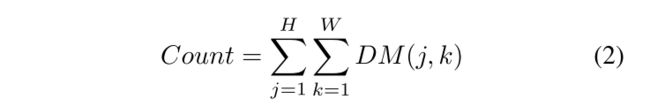
3.5. Loss Function
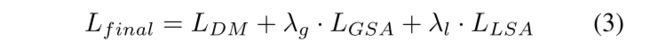
损失函数包含三个部分, L D M L_{DM} LDM是在预测密度图上定义的损失函数。这个loss是为了让预测得到的密度图接近ground truth密度图。我们还使用了两个辅助的损失 L G S A L_{GSA} LGSA和 L L S A L_{LSA} LLSA,这两个损失将让预测的全局和局部密度scale attention分别接近于真实的全局和局部scale。参数 λ g λ_g λg和 λ l λ_l λl用来控制两个辅助loss的贡献度。接下来,我们详细介绍损失函数。
![]()
L G S A L_{GSA} LGSA是用于使预测得到的global scale attention scores接近于ground truth,我们按照下面的方式获得ground-truth global scale attention。
首先,在训练数据中找到count的最大值和最小值,记为 C o u n t m a x Count_{max} Countmax和 C o u n t m i n Count_{min} Countmin,我们将范围 [ C o u n t m i n , C o u n t m a x ] [Count_{min},Count_{max}] [Countmin,Countmax]分为三个大小相等的距离。对于一张训练图片,根据ground truth crowd counting落入那一段,我们假设ground truth global scale为 g g t g_{gt} ggt, g g t g_{gt} ggt属于 { 1 , 2 , 3 } \{1,2,3\} {1,2,3}。令 g ∈ R 3 g∈R^3 g∈R3是该训练图像上全局注意力分数(对应于3个不同尺度)的向量。我们使用标准交叉熵损失定义 L G S A L_{GSA} LGSA为 L G S A = C E ( g , g g t ) L_{GSA} = CE(g,g_{gt}) LGSA=CE(g,ggt),其中 C E ( ⋅ ) CE(·) CE(⋅)表示多类交叉熵损失函数。
L L S A L_{LSA} LLSA用于使图像上每个空间位置处的预测local scale与训练图像上的ground truth local scale一致。我们按照下列的方法生成ground-truth local scale。对于训练图像中的像素位置,我们通过对该位置的64×64邻域中的ground truth密度图求和,得出该位置的局部人群计数。然后,我们在训练图像上找到局部人群数量的最小值/最大值。同样,我们将范围划分为三段,并根据本地人群计数(超过64×64邻域)所属的bin在像素位置分配ground truth。 l g t ∈ R H × W l_{gt} ∈ R^{H×W} lgt∈RH×W作为训练图片的ground truth local scale,每个项 l g t l_{gt} lgt ( l g t ∈ 1 , 2 , 3 ) (_{lg}t∈{1,2,3}) (lgt∈1,2,3)表示相应空间位置处的ground truth scale。 l ∈ R H × W × 3 l ∈ R^{H×W×3} l∈RH×W×3表示预测得到的local scale attention。我们定义 L L S A L_{LSA} LLSA为所有空间位置的交叉熵求和,如下所示
![]()