Python时间序列处理之ARIMA模型的使用讲解
今天小编就为大家分享一篇关于Python时间序列处理之ARIMA模型的使用讲解,小编觉得内容挺不错的,现在分享给大家,具有很好的参考价值,需要的朋友一起跟随小编来看看吧
ARIMA模型
ARIMA模型的全称是自回归移动平均模型,是用来预测时间序列的一种常用的统计模型,一般记作ARIMA(p,d,q)。
ARIMA的适应情况
ARIMA模型相对来说比较简单易用。在应用ARIMA模型时,要保证以下几点:
时间序列数据是相对稳定的,总体基本不存在一定的上升或者下降趋势,如果不稳定可以通过差分的方式来使其变稳定。
非线性关系处理不好,只能处理线性关系
判断时序数据稳定
基本判断方法:稳定的数据,总体上是没有上升和下降的趋势的,是没有周期性的,方差趋向于一个稳定的值。
ARIMA数学表达
ARIMA(p,d,q),其中p是数据本身的滞后数,是AR模型即自回归模型中的参数。d是时间序列数据需要几次差分才能得到稳定的数据。q是预测误差的滞后数,是MA模型即滑动平均模型中的参数。
a) p参数与AR模型
AR模型描述的是当前值与历史值之间的关系,滞后p阶的AR模型可以表示为: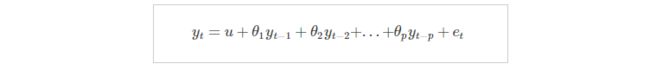
其中u是常数,et代表误差。
b) q参数与MA模型
MA模型描述的是当前值与自回归部分的误差累计的关系,滞后q阶的MA模型可以表示为: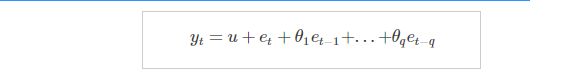
其中u是常数,et代表误差。
c) d参数与差分
一阶差分: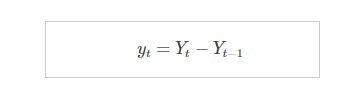
二阶差分: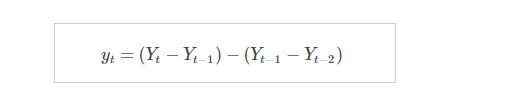
d) ARIMA = AR+MA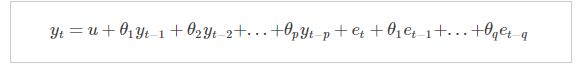
ARIMA模型使用步骤
获取时间序列数据
观测数据是否为平稳的,否则进行差分,化为平稳的时序数据,确定d
通过观察自相关系数ACF与偏自相关系数PACF确定q和p
得到p,d,q后使用ARIMA(p,d,q)进行训练预测
Python调用ARIMA
#差分处理
diff_series = diff_series.diff(1)#一阶
diff_series2 = diff_series.diff(1)#二阶
#ACF与PACF
#从scipy导入包
from scipy import stats
import statsmodels.api as sm
#画出acf和pacf
sm.graphics.tsa.plot_acf(diff_series)
sm.graphics.tsa.plot_pacf(diff_series)
#arima模型
from statsmodels.tsa.arima_model import ARIMA
model = ARIMA(train_data,order=(p,d,q),freq='')#freq是频率,根据数据填写
arima = model.fit()#训练
print(arima)
pred = arima.predict(start='',end='')#预测
推荐我们的Python学习扣qun:913066266 ,看看前辈们是如何学习的!从基础的python脚本到web开发、爬虫、django、数据挖掘等【PDF,实战源码】,零基础到项目实战的资料都有整理。送给每一位python的小伙伴!每天都有大牛定时讲解Python技术,分享一些学习的方法和需要注意的小细节,点击加入我们的 python学习者聚集地
总结
以上就是这篇文章的全部内容了,希望本文的内容对大家的学习或者工作具有一定的参考学习价值