Python基础学习笔记-11.Numpy库

11.Numpy库

11.1.Numpy概述

低效的Python for循环

【例】 求100万个数的倒数

def compute_reciprocals(values):

    res = []

    for value in values:      # 每遍历到一个元素，就要判断其类型，并查找适用于该数据类型的正确函数

        res.append(1/value)

    return res

 

values = list(range(1, 1000000))

%timeit compute_reciprocals(values)

145 ms ± 13.7 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

%timeit ：ipython中统计运行时间的魔术方法（多次运行取平均值）

import numpy as np

values = np.arange(1, 1000000)

%timeit 1/values

5.99 ms ± 33.9 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

实现相同计算，Numpy的运行速度是Python循环的25倍，产生了质的飞跃

Numpy为什么如此高效

Numpy 是由C语言编写的

1、编译型语言VS解释型语言

C语言执行时，对代码进行整体编译，速度更快

2、连续单一类型存储VS分散多变类型存储

（1）Numpy数组内的数据类型必须是统一的，如全部是浮点型，而Python列表支持任意类型数据的填充

（2）Numpy数组内的数据连续存储在内存中，而Python列表的数据分散在内存中

  这种存储结构，与一些更加高效的底层处理方式更加的契合

3、多线程VS线程锁

Python语言执行时有线程锁，无法实现真正的多线程并行，而C语言可以

什么时候用Numpy

在数据处理的过程中，遇到使用“Python for循环” 实现一些向量化、矩阵化操作的时候，要优先考虑用Numpy

如： 1、两个向量的点乘

    2、矩阵乘法

11.2.Numpy数组的创建

11.2.1.从列表开始创建

import numpy as np

x = np.array([1, 2, 3, 4, 5])

print(x)

[1 2 3 4 5]

print(type(x))

print(x.shape)

(5,)

设置数组的数据类型

x = np.array([1, 2, 3, 4, 5], dtype="float32")

print(x)

print(type(x[0]))

[1. 2. 3. 4. 5.]

二维数组

x = np.array([[1, 2, 3],

             [4, 5, 6],

             [7, 8, 9]])

print(x)

print(x.shape)

[[1 2 3]

 [4 5 6]

 [7 8 9]]

(3, 3)

11.2.2.从头创建数组

（1）创建长度为5的数组，值都为0

np.zeros(5, dtype=int)

array([0, 0, 0, 0, 0])

（2）创建一个2*4的浮点型数组，值都为1

np.ones((2, 4), dtype=float)

array([[1., 1., 1., 1.],

       [1., 1., 1., 1.]])

（3）创建一个3*5的数组，值都为8.8

np.full((3, 5), 8.8)

array([[8.8, 8.8, 8.8, 8.8, 8.8],

       [8.8, 8.8, 8.8, 8.8, 8.8],

       [8.8, 8.8, 8.8, 8.8, 8.8]])

（4）创建一个3*3的单位矩阵

np.eye(3)

array([[1., 0., 0.],

       [0., 1., 0.],

       [0., 0., 1.]])

（5）创建一个线性序列数组，从1开始，到15结束，步长为2

np.arange(1, 15, 2)

array([ 1,  3,  5,  7,  9, 11, 13])

（6）创建一个4个元素的数组，这四个数均匀的分配到0~1

np.linspace(0, 1, 4)

array([0.        , 0.33333333, 0.66666667, 1.        ])

（7）创建一个10个元素的数组，形成1~10^9的等比数列

np.logspace(0, 9, 10)

array([1.e+00, 1.e+01, 1.e+02, 1.e+03, 1.e+04, 1.e+05, 1.e+06, 1.e+07,

       1.e+08, 1.e+09])

（8）创建一个3*3的，在0~1之间均匀分布的随机数构成的数组

np.random.random((3,3))

array([[0.24347952, 0.41715541, 0.41363866],

       [0.44869706, 0.18128167, 0.18568051],

       [0.05705023, 0.0689205 , 0.74837661]])

（9）创建一个3*3的，均值为0，标准差为1的正态分布随机数构成的数组

np.random.normal(0, 1, (3,3))

array([[-0.38530465,  0.17474932,  0.31129291],

       [ 1.61626424, -2.18883854,  0.54043825],

       [-0.9141666 , -0.03804043, -0.6645122 ]])

（10）创建一个3*3的，在[0,10)之间随机整数构成的数组

np.random.randint(0, 10, (3,3))

array([[9, 1, 9],

       [0, 3, 9],

       [8, 5, 4]])

（11）随机重排列

x = np.array([10, 20, 30, 40])

np.random.permutation(x)       # 生产新列表

array([20, 40, 10, 30])

print(x)

np.random.shuffle(x)          # 修改原列表

print(x)

[10 20 30 40]

[20 40 10 30]

（12）随机采样

按指定形状采样

x = np.arange(10, 25, dtype = float)

x

array([10., 11., 12., 13., 14., 15., 16., 17., 18., 19., 20., 21., 22.,

       23., 24.])

np.random.choice(x, size=(4, 3))

array([[19., 23., 22.],

       [22., 21., 13.],

       [15., 21., 17.],

       [14., 23., 19.]])

import numpy as np

np.random.choice(10, 10)

array([0, 0, 9, 5, 8, 5, 2, 4, 9, 8])

x = np.arange(5).reshape(1, 5)

x

x.sum(axis=1, keepdims=True)

array([[10]])

按概率采样

np.random.choice(x, size=(4, 3), p=x/np.sum(x))

array([[15., 21., 20.],

       [23., 17., 18.],

       [23., 15., 17.],

       [19., 24., 22.]])

11.3.Numpy数组的性质

11.3.1.数组的属性

1、数组的形状shape

x = np.random.randint(10, size=(3, 4))

x

array([[5, 5, 2, 7],

       [2, 3, 0, 8],

       [3, 8, 1, 7]])

x.shape

(3, 4)

2、数组的维度ndim

x.ndim

2

y = np.arange(10)

y

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

y.ndim

1

3、数组的大小size

x.size

12

4、数组的数据类型dtype

x.dtype

dtype('int32')

11.3.2.数组索引

1、一维数组的索引

x1 = np.arange(10)

x1

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

x1[0]

0

x1[5]

5

x1[-1]

9

2、多维数组的索引——以二维为例

x2 = np.random.randint(0, 20, (2,3))

x2

array([[11,  3, 11],

       [ 6,  1,  5]])

x2[0, 0]

11

x2[0][0]

11

注意：numpy数组的数据类型是固定的，向一个整型数组插入一个浮点值，浮点值会向下进行取整

x2[0, 0] = 1.618

x2

array([[ 1,  3, 11],

       [ 6,  1,  5]])

11.3.3.数组的切片

1、一维数组——跟列表一样

x1 = np.arange(10)

x1

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

x1[:3]

array([0, 1, 2])

x1[3:]

array([3, 4, 5, 6, 7, 8, 9])

x1[::-1]

array([9, 8, 7, 6, 5, 4, 3, 2, 1, 0])

2、多维数组——以二维为例

x2 = np.random.randint(20, size=(3,4))

x2

array([[14,  9, 15,  8],

       [18,  8, 16, 17],

       [ 0,  8,  2, 17]]

x2[:2, :3]             # 前两行，前三列

array([[14,  9, 15],

       [18,  8, 16]])

x2[:2, 0:3:2]       # 前两行 前三列（每隔一列）

array([[14, 15],

       [18, 16]])

x2[::-1, ::-1]

array([[17,  2,  8,  0],

       [17, 16,  8, 18],

       [ 8, 15,  9, 14]])

3、获取数组的行和列

x3 = np.random.randint(20, size=(3,4))

x3

array([[ 8, 13, 15,  7],

       [19, 13, 17,  6],

       [11,  2,  0, 12]])

x3[1, :]   #第一行  从0开始计数

array([19, 13, 17,  6])

x3[1]    # 第一行简写

array([19, 13, 17,  6])

x3[:, 2]  # 第二列   从0开始计数

array([15, 17,  0])

4、切片获取的是视图，而非副本

x4 = np.random.randint(20, size=(3,4))

x4

array([[ 5, 14,  7,  2],

       [ 8, 12,  9,  3],

       [19,  0, 10,  7]])

x5 = x4[:2, :2]

x5

array([[ 5, 14],

       [ 8, 12]])

注意：视图元素发生修改，则原数组亦发生相应修改

x5[0, 0] = 0

x5

array([[ 0, 14],

       [ 8, 12]])

x4

array([[ 0, 14,  7,  2],

       [ 8, 12,  9,  3],

       [19,  0, 10,  7]])

5、修改切片的安全方式：copy

x4 = np.random.randint(20, size=(3,4))

x4

array([[18, 14, 10, 12],

       [10, 16,  7, 19],

       [ 3, 16,  3, 12]])

x6 = x4[:2, :2].copy()

x6

array([[18, 14],

       [10, 16]])

x6[0, 0] = 0

x6

array([[ 0, 14],

       [10, 16]])

x4

array([[18, 14, 10, 12],

       [10, 16,  7, 19],

       [ 3, 16,  3, 12]])

11.3.4.数组的变形

x5 = np.random.randint(0, 10, (12,))

x5

array([9, 8, 5, 9, 2, 6, 2, 9, 4, 5, 1, 7])

x5.shape

(12,)

x6 = x5.reshape(3, 4)

x6

array([[9, 8, 5, 9],

       [2, 6, 2, 9],

       [4, 5, 1, 7]])

注意：reshape返回的是视图，而非副本

x6[0, 0] = 0

x5

array([0, 8, 5, 9, 2, 6, 2, 9, 4, 5, 1, 7])

一维向量转行向量

x7 = x5.reshape(1, x5.shape[0])    

x7

array([[0, 8, 5, 9, 2, 6, 2, 9, 4, 5, 1, 7]])

x8 = x5[np.newaxis, :] #np.newaxis表示增加一个维度

x8

array([[0, 8, 5, 9, 2, 6, 2, 9, 4, 5, 1, 7]])

一维向量转列向量

x7 = x5.reshape(x5.shape[0], 1)    

x7

array([[0],

       [8],

        ...

       [7]])

x8 = x5[:, np.newaxis]

x8

array([[0],

       [8],

        ...

       [7]])

多维向量转一维向量

x6 = np.random.randint(0, 10, (3, 4))

x6

array([[3, 7, 6, 4],

       [4, 5, 6, 3],

       [7, 6, 2, 3]])

flatten返回的是副本

x9 = x6.flatten()

x9

array([3, 7, 6, 4, 4, 5, 6, 3, 7, 6, 2, 3])

x9[0]=0

x6

array([[3, 7, 6, 4],

       [4, 5, 6, 3],

       [7, 6, 2, 3]])

ravel返回的是视图

x10 = x6.ravel()

x10

array([3, 7, 6, 4, 4, 5, 6, 3, 7, 6, 2, 3])

x10[0]=0

x6

array([[0, 7, 6, 4],

       [4, 5, 6, 3],

       [7, 6, 2, 3]])

reshape返回的是视图

x11 = x6.reshape(-1)

x11

array([0, 7, 6, 4, 4, 5, 6, 3, 7, 6, 2, 3])

x11[0]=10

x6

array([[10,  7,  6,  4],

       [ 4,  5,  6,  3],

       [ 7,  6,  2,  3]])

11.3.5.数组的拼接

x1 = np.array([[1, 2, 3],

              [4, 5, 6]])

x2 = np.array([[7, 8, 9],

              [0, 1, 2]])

1、水平拼接——非视图

x3 = np.hstack([x1, x2])

x3

array([[1, 2, 3, 7, 8, 9],

       [4, 5, 6, 0, 1, 2]])

x3[0][0] = 0

x1

array([[1, 2, 3],

       [4, 5, 6]])

x4 = np.c_[x1, x2]

x4

array([[1, 2, 3, 7, 8, 9],

       [4, 5, 6, 0, 1, 2]])

x4[0][0] = 0

x1

array([[1, 2, 3],

       [4, 5, 6]])

2、垂直拼接——非视图

x1 = np.array([[1, 2, 3],

              [4, 5, 6]])

x2 = np.array([[7, 8, 9],

              [0, 1, 2]])

x5 = np.vstack([x1, x2])

x5

array([[1, 2, 3],

       [4, 5, 6],

       [7, 8, 9],

       [0, 1, 2]])

x6 = np.r_[x1, x2]

x6

array([[1, 2, 3],

       [4, 5, 6],

       [7, 8, 9],

       [0, 1, 2]])

11.3.6.数组的分裂

1、split的用法

x6 = np.arange(10)

x6

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

x1, x2, x3 = np.split(x6, [2, 7])

print(x1, x2, x3)

[0 1] [2 3 4 5 6] [7 8 9]

2、hsplit的用法

x7 = np.arange(1, 26).reshape(5, 5)

x7

array([[ 1,  2,  3,  4,  5],

       [ 6,  7,  8,  9, 10],

       [11, 12, 13, 14, 15],

       [16, 17, 18, 19, 20],

       [21, 22, 23, 24, 25]])

left, middle, right = np.hsplit(x7, [2,4])

print("left:\n", left)            # 第0~1列

print("middle:\n", middle)        # 第2~3列

print("right:\n", right)          # 第4列

left:

 [[ 1  2]

 [ 6  7]

 [11 12]

 [16 17]

 [21 22]]

middle:

 [[ 3  4]

 [ 8  9]

 [13 14]

 [18 19]

 [23 24]]

right:

 [[ 5]

 [10]

 [15]

 [20]

 [25]]

3、vsplit的用法

x7 = np.arange(1, 26).reshape(5, 5)

x7

array([[ 1,  2,  3,  4,  5],

       [ 6,  7,  8,  9, 10],

       [11, 12, 13, 14, 15],

       [16, 17, 18, 19, 20],

       [21, 22, 23, 24, 25]])

upper, middle, lower = np.vsplit(x7, [2,4])

print("upper:\n", upper)         # 第0~1行

print("middle:\n", middle)       # 第2~3行

print("lower:\n", lower)         # 第4行

upper:

 [[ 1  2  3  4  5]

 [ 6  7  8  9 10]]

middle:

 [[11 12 13 14 15]

 [16 17 18 19 20]]

lower:

 [[21 22 23 24 25]]

11.4.Numpy四大运算

11.4.1.向量化运算

1、与数字的加减乘除等

x1 = np.arange(1,6)

x1

array([1, 2, 3, 4, 5])

print("x1+5", x1+5)

print("x1-5", x1-5)

print("x1*5", x1*5)

print("x1/5", x1/5)

x1+5 [ 6  7  8  9 10]

x1-5 [-4 -3 -2 -1  0]

x1*5 [ 5 10 15 20 25]

x1/5 [0.2 0.4 0.6 0.8 1. ]

print("-x1", -x1)

print("x1**2", x1**2)

print("x1//2", x1//2)

print("x1%2", x1%2)

-x1 [-1 -2 -3 -4 -5]

x1**2 [ 1  4  9 16 25]

x1//2 [0 1 1 2 2]

x1%2 [1 0 1 0 1]

2、绝对值、三角函数、指数、对数

（1）绝对值

x2 = np.array([1, -1, 2, -2, 0])

x2

array([ 1, -1,  2, -2,  0])

abs(x2)

array([1, 1, 2, 2, 0])

np.abs(x2)

array([1, 1, 2, 2, 0])

（2）三角函数

theta = np.linspace(0, np.pi, 3)

theta

array([0.        , 1.57079633, 3.14159265])

print("sin(theta)", np.sin(theta))

print("con(theta)", np.cos(theta))

print("tan(theta)", np.tan(theta))

sin(theta) [0.0000000e+00 1.0000000e+00 1.2246468e-16]

con(theta) [ 1.000000e+00  6.123234e-17 -1.000000e+00]

tan(theta) [ 0.00000000e+00  1.63312394e+16 -1.22464680e-16]

x = [1, 0 ,-1]

print("arcsin(x)", np.arcsin(x))

print("arccon(x)", np.arccos(x))

print("arctan(x)", np.arctan(x))

arcsin(x) [ 1.57079633  0.         -1.57079633]

arccon(x) [0.         1.57079633 3.14159265]

arctan(x) [ 0.78539816  0.         -0.78539816]

（3）指数运算

x = np.arange(3)

x

array([0, 1, 2])

np.exp(x)

array([1.        , 2.71828183, 7.3890561 ])

（4）对数运算

x = np.array([1, 2, 4, 8 ,10])

print("ln(x)", np.log(x))

print("log2(x)", np.log2(x))

print("log10(x)", np.log10(x))

ln(x) [0.         0.69314718 1.38629436 2.07944154 2.30258509]

log2(x) [0.         1.         2.         3.         3.32192809]

log10(x) [0.         0.30103    0.60205999 0.90308999 1.        ]

3、两个数组的运算

x1 = np.arange(1,6)

x1

array([1, 2, 3, 4, 5])

x2 = np.arange(6,11)

x2

array([ 6,  7,  8,  9, 10])

print("x1+x2:", x1+x2)

print("x1-x2:", x1-x2)

print("x1*x2:", x1*x2)

print("x1/x2:", x1/x2)

x1+x2: [ 7  9 11 13 15]

x1-x2: [-5 -5 -5 -5 -5]

x1*x2: [ 6 14 24 36 50]

x1/x2: [0.16666667 0.28571429 0.375      0.44444444 0.5       ]

11.4.2.矩阵运算

x = np.arange(9).reshape(3, 3)

x

array([[0, 1, 2],

       [3, 4, 5],

       [6, 7, 8]])

矩阵的转置

y = x.T

y

array([[0, 3, 6],

       [1, 4, 7],

       [2, 5, 8]])

矩阵乘法

x = np.array([[1, 0],

             [1, 1]])

y = np.array([[0, 1],

             [1, 1]])

x.dot(y)

array([[0, 1],

       [1, 2]])

np.dot(x, y)

array([[0, 1],

       [1, 2]])

y.dot(x)

array([[1, 1],

       [2, 1]])

np.dot(y, x)

array([[1, 1],

       [2, 1]])

注意跟x*y的区别

x*y

array([[0, 0],

       [1, 1]])

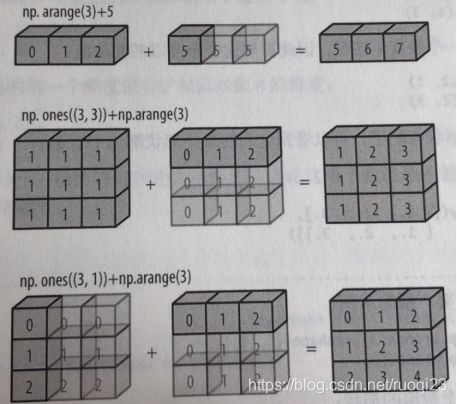
11.4.3.广播运算

x = np.arange(3).reshape(1, 3)

x

array([[0, 1, 2]])

x+5

array([[5, 6, 7]])

规则

如果两个数组的形状在维度上不匹配

那么数组的形式会沿着维度为1的维度进行扩展以匹配另一个数组的形状。

x1 = np.ones((3,3))

x1

array([[1., 1., 1.],

       [1., 1., 1.],

       [1., 1., 1.]])

x2 = np.arange(3).reshape(1, 3)

x2

array([[0, 1, 2]])

x1+x2

array([[1., 2., 3.],

       [1., 2., 3.],

       [1., 2., 3.]])

x3 = np.logspace(1, 10, 10, base=2).reshape(2, 5)

x3

array([[   2.,    4.,    8.,   16.,   32.],

       [  64.,  128.,  256.,  512., 1024.]])

x4 = np.array([[1, 2, 4, 8, 16]])

x4

array([[ 1,  2,  4,  8, 16]])

x3/x4

array([[ 2.,  2.,  2.,  2.,  2.],

       [64., 64., 64., 64., 64.]])

x5 = np.arange(3).reshape(3, 1)

x5

array([[0],

       [1],

       [2]])

x6 = np.arange(3).reshape(1, 3)

x6

array([[0, 1, 2]])

x5+x6

array([[0, 1, 2],

       [1, 2, 3],

       [2, 3, 4]])

11.4.4.比较运算和掩码

1、比较运算

x1 = np.random.randint(30, size=(3,10))

x1

array([[37, 44, 58, 79,  1, 24, 85, 90, 27, 56],

       [74, 68, 88, 27, 46, 34, 92,  1, 35, 45],

       [36, 31, 45, 39, 66, 82, 42, 25, 33, 84]])

x1 > 50

array([[False, False,  True,  True, False, False,  True,  True, False, True],

       [ True,  True,  True, False, False, False,  True, False, False, False],

       [False, False, False, False,  True,  True, False, False, False, True]])

2、操作布尔数组

x2 = np.random.randint(10, size=(3, 4))

x2

array([[1, 4, 2, 9],

       [8, 8, 2, 4],

       [9, 5, 3, 6]])

print(x2 > 5)

np.sum(x2 > 5)

[[False False False  True]

 [ True  True False False]

 [ True False False  True]]

5

np.all(x2 > 0)

True

np.any(x2 == 6)

True

np.all(x2 < 9, axis=1)   # 按行进行判断

array([False,  True, False])

(x2 < 9) & (x2 >5)

array([[False, False, False, False],

       [ True,  True, False, False],

       [False, False, False,  True]])

np.sum((x2 < 9) & (x2 >5))

3

3、将布尔数组作为掩码

x2

array([[1, 4, 2, 9],

       [8, 8, 2, 4],

       [9, 5, 3, 6]])

x2 > 5

array([[False, False, False,  True],

       [ True,  True, False, False],

       [ True, False, False,  True]])

x2[x2 > 5]

array([9, 8, 8, 9, 6])

11.4.5.花式索引

1、一维数组

x = np.random.randint(100, size=10)

x

array([43, 69, 67,  9, 11, 27, 55, 93, 23, 82])

注意：结果的形状与索引数组ind一致

ind = [2, 6, 9]

x[ind]

array([67, 55, 82])

ind = np.array([[1, 0],

               [2, 3]])

x[ind]

array([[69, 43],

       [67,  9]])

2、多维数组

x = np.arange(12).reshape(3, 4)

x

array([[ 0,  1,  2,  3],

       [ 4,  5,  6,  7],

       [ 8,  9, 10, 11]])

row = np.array([0, 1, 2])

col = np.array([1, 3, 0])

x[row, col]               # x(0, 1) x(1, 3) x(2, 0)

array([1, 7, 8])

row[:, np.newaxis]       # 列向量

array([[0],

       [1],

       [2]])

x[row[:, np.newaxis], col]    # 广播机制

array([[ 1,  3,  0],

       [ 5,  7,  4],

       [ 9, 11,  8]])

11.5.其他Numpy通用函数

11.5.1.数值排序

x = np.random.randint(20, 50, size=10)

x

array([48, 27, 44, 24, 34, 21, 24, 30, 34, 46])

产生新的排序数组

np.sort(x)

array([21, 24, 24, 27, 30, 34, 34, 44, 46, 48])

x

array([48, 27, 44, 24, 34, 21, 24, 30, 34, 46])

替换原数组

x.sort()

x

array([21, 24, 24, 27, 30, 34, 34, 44, 46, 48])

获得排序索引

x = np.random.randint(20, 50, size=10)

x

array([27, 36, 35, 28, 34, 20, 21, 49, 48, 30])

i = np.argsort(x)

i

array([5, 6, 0, 3, 9, 4, 2, 1, 8, 7], dtype=int64)

11.5.2.最大最小值

x = np.random.randint(20, 50, size=10)

x

array([48, 31, 30, 44, 48, 33, 44, 48, 39, 35])

print("max:", np.max(x))

print("min:", np.min(x))

max: 48

min: 30

print("max_index:", np.argmax(x))

print("min_index:", np.argmin(x))

max_index: 0

min_index: 2

11.5.3.数值求和、求积

x = np.arange(1,6)

x

array([1, 2, 3, 4, 5])

x.sum()

15

np.sum(x)

15

x1 = np.arange(6).reshape(2,3)

x1

array([[0, 1, 2],

       [3, 4, 5]])

按行求和

np.sum(x1, axis=1)

array([ 3, 12])

按列求和

np.sum(x1, axis=0)

array([3, 5, 7])

全体求和

np.sum(x1)

15

求积

x.prod()

120

np.prod(x)

120

11.5.4.中位数、均值、方差、标准差

x = np.random.normal(0, 1, size=10000)

import matplotlib.pyplot as plt

plt.hist(x, bins=50)

plt.show()

中位数

np.median(x)

-0.01024418366119727

均值

x.mean()

-0.004164442327293362

np.mean(x)

-0.004164442327293362

方差

x.var()

1.0221853234535774

np.var(x)

1.0221853234535774

标准差

x.std()

1.0110318112965473

np.std(x)

1.0110318112965473

11.6.作业练习

numpy数组的创建和性质：

1、创建一个4*6的二维数组，元素由0~1之间均匀分布的随机数构成，输出其形状、大小、维度和数据类型。

2、将（1）中的二维数组分别转换为3*8的数组和摊平为一维数组。

3、创建2个4*4的二维数组，元素为整数，随机取自区间[0, 10)，请将两个数组分别进行水平拼接和垂直拼接。

4、创建一个6*16的数组，其中，数组的外围均为1，内部均为0，提示：用到切片赋值。

numpy四大运算和通用函数：

5、创建一个由10000个元素构成的一维数组，元素随机取自[0, 100)

l 求数组元素的均值、方差和标准差；

l 通过 (x-x.mean)/x.std的方法，将数组归一化。

l 求数组的最大值和最小值，并获取其索引位置；

l 通过 (x-x.min)/(x.max-x.min)的方法，将数组归一化。

6、创建一个由30个元素构成的一维数组，元素随机取自[80, 100)

l 获得大于等于95分的成绩；

l 获得小于等于85分的成绩；

l 获得大于85分，小于95分的成绩；

l 对成绩进行排序。

7、构建两个3*3的二维列表A和B

（1）乘法运算

l 用Python for循环实现A*B的乘法运算；

l 用Numpy 实现A*B 的乘法运算；

l 对比两种实现方式的运行时间。

（2）矩阵乘法

l 用Python for循环实现A和B的矩阵乘法；

l 用Numpy实现np.dot(A, B)的矩阵乘法；

l 对比两种实现方式的运行时间。

（3）对比矩阵乘法跟乘法运算的不同。

 

答案：

import numpy as np

import random

1.

arr = np.random.random((4, 6))

print(arr)

print("shape = {}, size = {}, dimension = {}, dtype = {}"

      .format((arr.shape[0], arr.shape[1]), arr.size, arr.ndim, arr.dtype))

[[0.87234165 0.76793816 0.20329659 0.67588528 0.39278516 0.30852181]

 [0.3722015  0.17675793 0.01827887 0.33450565 0.22872758 0.35906343]

 [0.4448989  0.0355992  0.88128631 0.40998858 0.31613782 0.61468709]

 [0.80893753 0.20962329 0.84701968 0.61099015 0.50922118 0.65357641]]

shape = (4, 6), size = 24, dimension = 2, dtype = float64

2.

print(arr.reshape(3, 8))

[[0.87234165 0.76793816 0.20329659 0.67588528 0.39278516 0.30852181

  0.3722015  0.17675793]

 [0.01827887 0.33450565 0.22872758 0.35906343 0.4448989  0.0355992

  0.88128631 0.40998858]

 [0.31613782 0.61468709 0.80893753 0.20962329 0.84701968 0.61099015

  0.50922118 0.65357641]]

print(arr.reshape(-1))

[0.87234165 0.76793816 0.20329659 0.67588528 0.39278516 0.30852181

 0.3722015  0.17675793 0.01827887 0.33450565 0.22872758 0.35906343

 0.4448989  0.0355992  0.88128631 0.40998858 0.31613782 0.61468709

 0.80893753 0.20962329 0.84701968 0.61099015 0.50922118 0.65357641]

3.

arr2 = np.random.randint(0, 10, (4, 4))

arr3 = np.random.randint(0, 10, (4, 4))

print("arr2 = \n{}".format(arr2))

print("arr3 = \n{}".format(arr3))

arr2 =

[[9 5 7 7]

 [2 5 2 9]

 [8 7 4 0]

 [4 1 5 3]]

arr3 =

[[9 0 5 1]

 [2 0 2 1]

 [5 5 5 1]

 [4 6 1 6]]

# 水平拼接

print(np.hstack([arr2, arr3]))

# 垂直拼接

print(np.vstack([arr2, arr3]))

[[9 5 7 7 9 0 5 1]

 [2 5 2 9 2 0 2 1]

 [8 7 4 0 5 5 5 1]

 [4 1 5 3 4 6 1 6]]

[[9 5 7 7]

 [2 5 2 9]

 [8 7 4 0]

 [4 1 5 3]

 [9 0 5 1]

 [2 0 2 1]

 [5 5 5 1]

 [4 6 1 6]]

4.

arr4 = np.zeros((6, 16))

# print(arr4)

arr4[0] = 1

arr4[:, 0] = 1

arr4[arr4.shape[0] - 1] = 1

arr4[:, arr4.shape[1] - 1] = 1

print(arr4)

[[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]

 [1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]

 [1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]

 [1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]

 [1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]

 [1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]]

5.

arr5 = np.random.randint(0, 100, 10000)

print(arr5)

[30 78 43 ... 39 99 11]

print("均值 = {}, 方差 = {}, 标准差 = {}".format(arr5.mean(), arr5.var(), arr5.std()))

均值 = 49.5523, 方差 = 830.88746471, 标准差 = 28.82511864173329

print((arr5 - arr5.mean()) / arr5.std())

[-0.6783077   0.98690661 -0.22731216 ... -0.36608002  1.71543787  -1.33745503]

# 最大值

print(arr5.max(), arr5.argmax())

# 最小值

print(arr5.min(), arr5.argmin())

99 190

0 34

print((arr5 - arr5.min()) / (arr5.max() - arr5.min()))

[0.3030303  0.78787879 0.43434343 ... 0.39393939 1.         0.11111111]

6.

score = np.random.randint(80, 100, 30)

print(score)

[89 90 97 96 83 97 92 82 98 90 86 99 94 98 98 91 91 85 98 81 98 82 86 84

 89 98 98 98 95 87]

print(score[score >= 95])

print(score[score <= 85])

[97 96 97 98 99 98 98 98 98 98 98 98 95]

[83 82 85 81 82 84]

score_over_85 = score[score > 85]

print(score_over_85[score_over_85 < 95])

# print(score[score > 85 and score < 95])

[89 90 92 90 86 94 91 91 86 89 87]

print(np.sort(score))

[81 82 82 83 84 85 86 86 87 89 89 90 90 91 91 92 94 95 96 97 97 98 98 98

 98 98 98 98 98 99]

7.

A = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]

B = [[3, 4, 8], [5, 2, 1], [4, 5, 9]]

print(A, B)

[[1, 2, 3], [4, 5, 6], [7, 8, 9]] [[3, 4, 8], [5, 2, 1], [4, 5, 9]]

# 乘法运算

import time

start_time = time.time()

for i in range(len(A)):

        for j  in range(len(B)):

            A[i][j] = A[i][j] * B[i][j]

end_time = time.time()                

print(start_time, end_time)

print("A = {}, the cost time is {}ms".format(A, (end_time - start_time) * 1000))

1571993538.380726 1571993538.381723

A = [[9, 32, 192], [100, 20, 6], [112, 200, 729]], the cost time is 0.9968280792236328ms

A = np.array(A)

B = np.array(B)

%timeit (A * B)

525 ns ± 29.6 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)

# 矩阵乘法

%timeit A.dot(B)

960 ns ± 24.1 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)

A.dot(B)

array([[ 955, 1060, 1832],

       [ 424,  470,  874],

       [4252, 4493, 7657]])

A = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]

B = [[3, 4, 8], [5, 2, 1], [4, 5, 9]]

def pro():

    res = [[0] * len(B[0]) for i in range(len(A))]

    for i in range(len(A)):

        for j in range(len(B[0])):

            for k in range(len(B)):

                res[i][j] += A[i][k] * B[k][j]

    return res

%timeit pro()

12.7 µs ± 83.1 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)