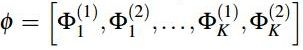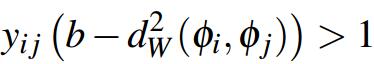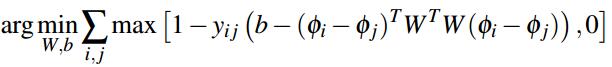人脸识别——DSIFT+Fisher Vecttor Coding
本次介绍的是一种传统的人脸识别方法《2013-BMVC-Fisher Vector Faces in the Wild》.
文章给出了数据和代码http://www.robots.ox.ac.uk/~vgg/software/face_desc/.
我自己的验证的时候使用的是VLfeat开源工具包,很好用:http://www.vlfeat.org/index.html
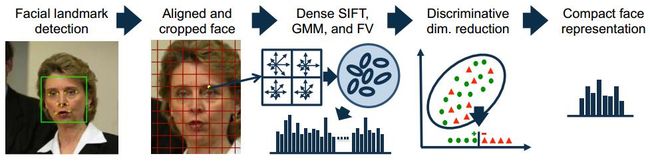
先来一个整个方法的流程图,然后再分步描述:
人脸特征表示
(1)Dense Sift with PCA
Dense Sift简称DSIFT,顾名思义,是一种密集采点的SIFT特征。传统的SIFT特征有一个选择关键点的过程,而DSIFT略过选点过程,而是在一定区域内类似滑动窗口一样密集选点并计算SIFT描述子。
此外,我们还需要回顾一下一个128维的SIFT算子是怎么来的,如下图(该图来自于Rachel-Zhang博客):
![]()
首先,选定一个关键点之后,我们会划定一个框,该框水平方向有4个bins,垂直方向也有4个bins,即该框包含了16个区域,每个区域又是一个\(4\times 4\)的块。我们在每个块里面统计8个方向的梯度,最终就可以得到\(16\times 8=128 \) 维的SIFT特征。由此可见,SIFT的维度是可以任意的,不一定非得是128。
文中作者以滑动步长1,滑动窗口\(24\times 24\) 密集的计算SIFT,同时按照\(\frac{1}{\sqrt{2}}\)的比例放缩图像,在不同尺度空间上重复上述过程。最终一副\(160\times 125\)大小的图片可以得到约2.6W个128维的SIFT。
由于数据量太大,不利用后续的编码学习,因此首先进行一次PCA将数据由128降维到64.
(2)Fisher Coding
Fisher Vector Coding有两个优点:(1)可以将特征映射到高维,这样特征易区分;(2)可以将不同数量的特征编码到同一长度,这一点对于我们的DSIFT尤其重要。
编码过程分为两步(首先需指定码字个数K):
(1)学习K个Gaussian Mixture Model (GMM)参数。
输入PCA之后的所有训练图片的特征\(64\times N\) ,输出K个均值\(\mu _k\)和K个方差\(\sigma _k\)以及K个后验概率\(\omega _k\)。这些参数其实描述的是整个训练集的分布,类似于我们通过Kmeans得到的K个聚类中心。
(2) 编码
编码过程其实就是按照下式利用我们上一步得到的GMM参数来计算。其中\(N\)是一副图像所提取的SIFT特征个数,\(\alpha_p(k)\)是第\(p\)个SIFT特征\(x_p\)分配到第\(k\)个高斯中心的权重。
然后将上面的结果拼成一个矢量,就得到Fisher Coding的结果。
由上易知,编码之后的长度为\(2\times k\times d\), 其中\(k\)为高斯个数,\(d\)为特征维度。
编码可能还需要进一步做signed square-rooting and L2 normalisation。
(3)Spatial information
显然上面的SIFT特征是不带有空间信息的,而空间信息对于人脸识别又很重要。因此,作者在Fisher Coding编码之前,在降维后的64维的SIFT特征后面追加2个空间坐标信息,如下式:
其中\(S_{xy}\)是降维后的64维特征,\(w,h\)分别是图像宽高。
人脸识别
本文后续的识别方法是一种基于距离的识别(认证)方法,即相同身份距离小于一定阈值,不同身份距离大于一定阈值。
最终,目标就是学习一个线性投影矩阵\(W\in R^{p\times d}\), 其中\(p\ll d\)。
作用有两点:
(1)降维,之前编码后纬度太高;
(2)映射到欧氏距离可分的子空间从而提高识别性能。
距离约束如下,添加了1的余量:
其中,\(b\) 是阈值,身份相同时 \(y_{ij}=1\), \(d\)表示欧氏距离.
\(p\) 维投影空间的欧氏距离可以看做原始\(d\) 维空间的低秩马氏度量,即:
于是, Object Function为:
优化采用PCA初始化,然后使用梯度下降方法,具体可参考原文。