曼哈顿距离最小生成树&莫队算法
参考资料:https://www.cnblogs.com/CsOH/p/5904430.html
https://blog.csdn.net/huzecong/article/details/8576908
https://www.cnblogs.com/xzxl/p/7237246.html
https://www.cnblogs.com/Paul-Guderian/p/6933799.html
首先先看一下
曼哈顿距离最小生成树
一,简述曼哈顿距离最小生成树:
给定二维平面上的N个点,在两点之间连边的代价为其曼哈顿距离,求使所有点连通的最小代价。
朴素的算法可以用O(N2)的Prim,或者处理出所有边做Kruskal,但在这里总边数有O(N2)条,所以Kruskal的复杂度变成了O(N2logN)。
事实上,真正有用的边远没有O(N2)条。我们考虑每个点会和其他一些什么样的点连边。
可以得出这样一个结论,以一个点为原点建立直角坐标系,在每45度内只会向距离该点最近的一个点连边。
证明:假设我们以点A为原点建系,考虑在y轴向右45度区域内的任意两点B(x1,y1)和C(x2,y2),不妨设|AB|≤|AC|(这里的距离为曼哈顿距离),如下图:
![]()
|AB|=x1+y1,|AC|=x2+y2,|BC|=|x1-x2|+|y1-y2|。而由于B和C都在y轴向右45度的区域内,有y-x>0且x>0。
下面我们分情况讨论:
1. x1>x2且y1>y2。这与|AB|≤|AC|矛盾;
2. x1≤x2且y1>y2。此时|BC|=x2-x1+y1-y2,|AC|-|BC|=x2+y2-x2+x1-y1+y2=x1-y1+2*y2。由前面各种关系可得y1>y2>x2>x1。假设|AC|<|BC|即y1>2*y2+x1,那么|AB|=x1+y1>2*x1+2*y2,|AC|=x2+y2<2*y2<|AB|与前提矛盾,故|AC|≥|BC|;
3. x1>x2且y1≤y2。与2同理;
4. x1≤x2且y1≤y2。此时显然有|AB|+|BC|=|AC|,即有|AC|>|BC|。
综上有|AC|≥|BC|,也即在这个区域内只需选择距离A最近的点向A连边。
这种连边方式可以保证边数是O(N)的,那么如果能高效处理出这些边,就可以用Kruskal在O(NlogN)的时间内解决问题。
下面我们就考虑怎样高效处理边。
我们只需考虑在一块区域内的点,其他区域内的点可以通过坐标变换“移动”到这个区域内。
为了方便处理,我们考虑在y轴向右45度的区域。
在某个点A(x0,y0)的这个区域内的点B(x1,y1)满足x1≥x0且y1-x1>y0-x0。这里对于边界我们只取一边,但是操作中两边都取也无所谓。那么|AB|=y1-y0+x1-x0=(x1+y1)-(x0+y0)。
在A的区域内距离A最近的点也即满足条件的点中x+y最小的点。因此我们可以将所有点按x坐标排序,再按y-x离散,用线段树或者树状数组维护大于当前点的y-x的最小的x+y对应的点。时间复杂度O(NlogN)。
至于坐标变换,一个比较好处理的方法是第一次直接做;第二次沿直线y=x翻转,即交换x和y坐标;第三次沿直线x=0翻转,即将x坐标取相反数;第四次再沿直线y=x翻转。注意只需要做4次,因为边是双向的。
至此,整个问题就可以在O(NlogN)的复杂度内解决了。
二、知识梳理
曼哈顿距离:给定二维平面上的N个点,在两点之间连边的代价。(即distance(P1,P2) = |x1-x2|+|y1-y2|)
曼哈顿距离最小生成树问题求什么?求使所有点连通的最小代价。
最小生成树的“环切”性质:在图G = (V, E)中,如果存在一个环,那么把环上的最大边e删除后得到的图G’ = (V, E- {e})的最小生成树的边权和与G相同。
三,简述算法
一个点把平面分成了8个部分:
![]()
由上面的废话可知,我们只需要让这个点与每个部分里距它最近的点连边。
拿R1来说吧:
![]()
如图,i的R1区域里距i最近的点是j。也就是说,其他点k都有:
xj + yj <= xk + yk
那么k将落在如下阴影部分:
![]()
显然,边(i,j), (j,k), (i,k)构成一个环
为了避免重复加边,我们只考虑R1~R4这4个区域。(总共加了4N条边)
这4个区域的点(x,y)要满足什么条件?
- 如果点(x,y)在R1,它要满足:x ≥ xi ,y – x ≥ yi – xi(最近点的x + y最小)
- 如果点(x,y)在R2,它要满足:y ≥ yi ,y – x ≤ yi – xi(最近点的x + y最小)
- 如果点(x,y)在R3,它要满足:y ≤ yi ,y + x ≥ yi + xi(最近点的y – x最小)
- 如果点(x,y)在R4,它要满足:x ≥ xi ,y + x ≤ yi – xi(最近点的y – x最小)
其中一个条件用排序,另一个条件用数据结构(这种方法很常用),在数据结构上询问,找最近点。因为询问总是前缀或后缀,所以可以用树状数组。
四,代码模板
//离散化:
scanf("%d", &N);
for (int i=1; i<=N; ++i)
{
scanf("%d%d", &P[i].x, &P[i].y);
P[i].id = i;
P[i].d = P[i].y - P[i].x;
P[i].s = P[i].y + P[i].x;
}
//对x,y离散化
int totxy = 0;
for (int i=1; i<=N; ++i)
{
xy[totxy++] = P[i].x;
xy[totxy++] = P[i].y;
}
sort(xy, xy+totxy);
for (int i=1; i<=N; ++i)
{
P[i].idx = lower_bound(xy, xy+totxy, P[i].x) - xy + 1;
P[i].idy = lower_bound(xy, xy+totxy, P[i].y) - xy + 1;
}//树状数组:
struct BIT
{
pii a[maxN * 2];
int N;
void Init(int _N)
{
N = _N;
for (int i=0; i<=N; ++i) a[i] = pii(oo, 0);
}
pii ask(int x)
{
return x == 0 ? pii(oo, 0) : min(a[x], ask(x - (x & (-x))));
}
void update(int x, const pii &v)
{
if (x > N) return ;
a[x] = min(a[x], v);
update(x + (x & (-x)), v);
}
pii ask_front(int x) {return ask(x);}
pii ask_back(int x) {return ask(N - x + 1);}
void update_front(int x, const pii &v) {update(x, v);}
void update_back(int x, const pii &v) {update(N - x + 1, v);}
} tree;
//构图:
bool cmp1(const Tpoint &A, const Tpoint &B)
{
//return A.x < B.x || (A.x == B.x && A.y < B.y);
return (A.y - A.x > B.y - B.x || A.y - A.x == B.y - B.x && A.x > B.x);
}
bool cmp2(const Tpoint &A, const Tpoint &B)
{
//return A.x < B.x || (A.x == B.x && A.y > B.y);
return (A.y + A.x < B.y + B.x || A.y + A.x == B.y + B.x && A.x > B.x);
}
bool cmp3(const Tpoint &A, const Tpoint &B)
{
//return A.y < B.y || (A.y == B.y && A.x < B.x);
return A.y - A.x < B.y - B.x || A.y - A.x == B.y - B.x && A.y > B.y;
}
bool cmp4(const Tpoint &A, const Tpoint &B)
{
//return A.y < B.y || (A.y == B.y && A.x > B.x);
return A.s > B.s || A.s == B.s && A.y < B.y;;
}
bool cmpE(const E_arr &A, const E_arr &B) {return A.v < B.v;}
void Make_Graph()
{
#define Connect(i,j) E[++tot_E].Init(P[i].id,P[j].id,getdis(i,j))
int LL, RR;
tree.Init(2 * N);
sort(P+1, P+N+1, cmp1);
for (int i=1; i<=N; ++i)
{
pii tmp = tree.ask_back(P[i].idx);
if (tmp.first < oo) Connect(i, tmp.second);
tree.update_back(P[i].idx, pii(P[i].x + P[i].y, i));
}
sort(P+1, P+N+1, cmp2);
tree.Init(2 * N);
for (int i=1; i<=N; ++i)
{
pii tmp = tree.ask_back(P[i].idx);
if (tmp.first < oo) Connect(i, tmp.second);
tree.update_back(P[i].idx, pii(P[i].x - P[i].y, i));
}
sort(P+1, P+N+1, cmp3);
tree.Init(2 * N);
for (int i=1; i<=N; ++i)
{
pii tmp = tree.ask_back(P[i].idy);
if (tmp.first < oo) Connect(i, tmp.second);
tree.update_back(P[i].idy, pii(P[i].x + P[i].y, i));
}
sort(P+1, P+N+1, cmp4);
tree.Init(2 * N);
for (int i=1; i<=N; ++i)
{
pii tmp = tree.ask_front(P[i].idy);
if (tmp.first < oo) Connect(i, tmp.second);
tree.update_front(P[i].idy, pii(P[i].x - P[i].y, i));
}
}五,实际应用
题目链接:http://poj.org/problem?id=3241
//POJ3241; Object Clustering; Manhattan Distance MST
#include
#include
#include
#define N 100000
#define INFI 123456789
struct point
{
int x, y, n;
bool operator < (const point &p) const
{ return x == p.x ? y < p.y : x < p.x; }
}p[N + 1];
struct inedge
{
int a, b, w;
bool operator < (const inedge &x) const
{ return w < x.w; }
}e[N << 3 | 1];
struct BITnode
{
int w, p;
}arr[N + 1];
int n, k, tot = 0, f[N + 1], a[N + 1], *l[N + 1], ans;
template
inline T abs(T x)
{ return x < (T)0 ? -x : x; }
int find(int x)
{ return x == f[x] ? x : f[x] = find(f[x]); }
inline bool cmp(int *a, int *b)
{ return *a < *b; }
inline int query(int x)
{
int r = INFI, p = -1;
for (; x <= n; x += x & -x)
if (arr[x].w < r) r = arr[x].w, p = arr[x].p;
return p;
}
inline void modify(int x, int w, int p)
{
for (; x > 0; x -= x & -x)
if (arr[x].w > w) arr[x].w = w, arr[x].p = p;
}
inline void addedge(int a, int b, int w)
{
++tot;
e[tot].a = a, e[tot].b = b, e[tot].w = w;
// printf("%d %d %d\n", a, b, w);
}
inline int dist(point &a, point &b)
{ return abs(a.x - b.x) + abs(a.y - b.y); }
int main()
{
//Initialize
scanf("%d%d", &n, &k);
for (int i = 1; i <= n; ++i)
{
scanf("%d%d", &p[i].x, &p[i].y);
p[i].n = i;
}
//Solve
for (int dir = 1; dir <= 4; ++dir)
{
//Coordinate transform - reflect by y=x and reflect by x=0
if (dir == 2 || dir == 4)
for (int i = 1; i <= n; ++i) p[i].x ^= p[i].y ^= p[i].x ^= p[i].y;
else if (dir == 3)
for (int i = 1; i <= n; ++i) p[i].x = -p[i].x;
//Sort points according to x-coordinate
std::sort(p + 1, p + n + 1);
//Discretize
for (int i = 1; i <= n; ++i) a[i] = p[i].y - p[i].x, l[i] = &a[i];
std::sort(l + 1, l + n + 1, cmp);
/*
int cnt = 1;
for (int i = 2; i <= n; ++i)
if (*l[i] != *l[i - 1]) *l[i - 1] = cnt++;
else *l[i - 1] = cnt;
*l[n] = cnt;
*/
for (int i = 1; i <= n; ++i) *l[i] = i;
//Initialize BIT
for (int i = 1; i <= n; ++i) arr[i].w = INFI, arr[i].p = -1;
//Find points and add edges
for (int i = n; i > 0; --i)
{
int pos = query(a[i]);
if (pos != -1)
addedge(p[i].n, p[pos].n, dist(p[i], p[pos]));
modify(a[i], p[i].x + p[i].y, i);
}
}
//Kruskal
std::sort(e + 1, e + tot + 1);
for (int i = 1; i <= n; ++i) f[i] = i;
for (int i = 1, ec = n; ec > k && i <= tot; ++i)
if (find(e[i].a) != find(e[i].b))
{
f[find(e[i].a)] = find(e[i].b);
if (--ec == k) ans = e[i].w;
}
printf("%d\n", ans);
return 0;
} 莫队算法
·排序巧妙优化复杂度,带来NOIP前的最后一丝宁静。几个活蹦乱跳的指针的跳跃次数,决定着莫队算法的优劣……
·目前的题型概括为三种:普通莫队,树形莫队以及带修莫队。
若谈及入门,那么BZOJ2038的美妙袜子一题堪称顶尖。
【例题一】袜子
·述大意:
进行区间询问[l,r],输出该区间内随机抽两次抽到相同颜色袜子的概率。
·分析:
首先考虑对于一个长度为n区间内的答案如何求解。题目要求Ans使用最简分数表示:那么分母就是n*n(表示两两袜子之间的随机组合),分子是一个累加和,累加的内容是该区间内每种颜色i出现次数sum[i]的平方。
将莫队算法抬上议程。莫队算法的思路是,离线情况下对所有的询问进行一个美妙的SORT(),然后两个指针l,r(本题是两个,其他的题可能会更多)不断以看似暴力的方式在区间内跳来跳去,最终输出答案。
掌握一个思想基础:两个询问之间的状态跳转。如图,当前完成的询问的区间为[a,b],下一个询问的区间为[p,q],现在保存[a,b]区间内的每个颜色出现次数的sum[]数组已经准备好,[a,b]区间询问的答案Ans1已经准备好,怎样用这些条件求出[p,q]区间询问的Ans2?
![]()
考虑指针向左或向右移动一个单位,我们要付出多大的代价才能维护sum[]和Ans(即使得sum[],Ans保存的是当前[l,r]的正确信息)。我们美妙地对图中l,r的向右移动一格进行分析:
![]()
如图啦。l指针向右移动一个单位,所造成的后果就是:我们损失了一个绿色方块。那么怎样维护?美妙地,sum[绿色]减去1。那Ans如何维护?先看分母,分母从n^2变成(n-1)^2,分子中的其他颜色对应的部分是不会变的,绿色却从sum[绿色]^2变成(sum[绿色]-1)^2 ,为了方便计算我们可以直接向给Ans减去以前该颜色的答案贡献(即sum[绿色]^2)再加上现在的答案贡献(即(sum[绿色]-1)2 )。同理,观赏下面的r指针移动,将是差不多的。
![]()
·如图r指针的移动带来的后果是,我们多了一个橙色方块。所以操作和上文相似,只不过是sum[橙色]++。
·回归正题地,我们美妙的发现,知道一个区间的信息,要求出旁边区间的信息(旁边区间指的是当前区间的一个指针通过加一减一得到的区间),竟只需要O(1)的时间。
·就算是这样,到这里为止的话莫队算法依旧无法焕发其光彩,原因是:如果我们以读入的顺序来枚举每个询问,每个询问到下一个询问时都用上述方法维护信息,那么在你脑海中会浮现出l,r跳来跳去的疯狂景象,疯狂之处在于最坏情况下时间复杂度为:O(n^2)————如果要这样玩,那不如写一个暴力程序。
·“莫队算法巧妙地将询问离线排序,使得其复杂度无比美妙……”在一般做题时我们时常遇到使用排序来优化枚举时间消耗的例子。莫队的优化基于分块思想:对于两个询问,若在其l在同块,那么将其r作为排序关键字,若l不在同块,就将l作为关键字排序(这就是双关键字)。大米饼使用Be[i]数组表示i所属的块是谁。排序如:
![]()
·值得强调的是,我们是在对询问进行操作。
·时间复杂度分析(分类讨论思想):
首先,枚举m个答案,就一个m了。设分块大小为unit。
分类讨论:
①l的移动:若下一个询问与当前询问的l所在的块不同,那么只需要经过最多2*unit步可以使得l成功到达目标.复杂度为:O(m*unit)
②r的移动:r只有在Be[l]相同时才会有序(其余时候还是疯狂地乱跳,你知道,一提到乱跳,那么每一次最坏就要跳n次!),Be[l]什么时候相同?在同一块里面l就Be[]相同。对于每一个块,排序执行了第二关键字:r。所以这里面的r是单调递增的,所以枚举完一个块,r最多移动n次。总共有n/unit个块:复杂度为:O(n*n/unit)
总结:O(n*unit+n*n/unit)(n,m同级,就统一使用n)
根据基本不等式得:当n为sqrt(n)时,得到莫队算法的真正复杂度:
O(n*sqrt(n))
·代码上来了(莫队喜欢while):
#include
#include
#include
#include
#include
#define go(i,a,b) for(int i=a;i<=b;i++)
#define mem(a,b) memset(a,b,sizeof(a))
#define ll long long
using namespace std;const int N=50003;
struct Mo{int l,r,ID;ll A,B;}q[N];ll S(ll x){return x*x;}
ll GCD(ll a,ll b){while(b^=a^=b^=a%=b);return a;}
int n,m,col[N],unit,Be[N];ll sum[N],ans;
bool cmp(Mo a,Mo b){return Be[a.l]==Be[b.l]?a.rq[i].l)revise(l-1,1),l--;
while(rq[i].r)revise(r,-1),r--;
if(q[i].l==q[i].r){q[i].A=0;q[i].B=1;continue;}
q[i].A=ans-(q[i].r-q[i].l+1);
q[i].B=1LL*(q[i].r-q[i].l+1)*(q[i].r-q[i].l);
ll gcd=GCD(q[i].A,q[i].B);q[i].A/=gcd;q[i].B/=gcd;
}
sort(q+1,q+m+1,CMP);
go(i,1,m)printf("%lld/%lld\n",q[i].A,q[i].B);
return 0;
}//Paul_Guderian 【例题二】数颜色
·述大意:
多个区间询问,询问[l,r]中颜色的种类数。可以单点修改颜色。
·分析:
莫队可以修改?那不是爆炸了吗。
这类爆炸的问题被称为带修莫队(可持久化莫队)。
按照美妙类比思想,可以引入一个“修改时间”,表示当前询问是发生在前Time个修改操作后的。也就是说,在进行莫队算法时,看看当前的询问和时间指针(第三个指针,别忘了l,r)是否相符,然后进行时光倒流或者时光推移操作来保证答案正确性。
·Sort的构造。仅靠原来的sort关键字会使得枚举每个询问都可能因为时间指针移动的缘故要移动n次,总共就n2次,那还不如写暴力。
·为了防止这样的事情发生,再加入第三关键字Tim:
![]()
·如何理解时间复杂度?
首先,R和Tim的关系就像L和R的关系一样:只有在前者处于同块时,后者才会得到排序的恩赐,否则sort会去满足前者,使得后者开始乱跳。
依旧像上文那样:枚举m个答案,就一个m了。设分块大小为unit。
分类讨论:
①对于l指针,依旧是O(unit*n)
②对于r指针,依旧是O(n*n/unit)
③对于T指针(即Time):
类比r时间复杂度的计算。我们要寻找有多少个单调段(一个单调段下来最多移动n次)。上文提到,当且仅当两个询问l在同块,r也在同块时,才会对可怜的Tim进行排序。局势明朗。对于每一个l的块,里面r最坏情况下占据了所有的块,所以最坏情况下:有n/unit个l的块,每个l的块中会有n/unit个r的块,此时,在一个r块里,就会出现有序的Tim。所以Tim的单调段个数为:(n/unit)*(n/unit)。每个单调段最多移动n次。
所以:O((n/unit)2*n)
三个指针汇总:O(unit*n+n2/unit+(n/unit)2*n)
·给你个大米饼代码:
#include
#include
#include
#define go(i,a,b) for(int i=a;i<=b;i++)
using namespace std;const int N=10003;
struct Query{int l,r,Tim,ID;}q[N];
struct Change{int pos,New,Old;}c[N];
int n,m,s[N],color[N*100],t,Time,now[N],unit,Be[N],ans[N],Ans,l=1,r,T;
bool cmp(Query a,Query b)
{
return Be[a.l]==Be[b.l]?(Be[a.r]==Be[b.r]?a.Tim0)Ans+=color[x]==1;if(d<0)Ans-=color[x]==0;}
void going(int x,int d){if(l<=x&&x<=r)revise(d,1),revise(s[x],-1);s[x]=d;}
int main(){
scanf("%d%d",&n,&m);unit=pow(n,0.666666);
go(i,1,n)scanf("%d",&s[i]),now[i]=s[i],Be[i]=i/unit+1;
go(i,1,m){char sign;int x,y;scanf(" %c %d%d",&sign,&x,&y);
if(sign=='Q')q[++t]=(Query){x,y,Time,t};
if(sign=='R')c[++Time]=(Change){x,y,now[x]},now[x]=y;
}
sort(q+1,q+t+1,cmp);go(i,1,t)
{
while(Tq[i].Tim)going(c[T].pos,c[T].Old),T--;
while(lq[i].l)revise(s[l-1],1),l--;
while(rq[i].r)revise(s[r],-1),r--;
ans[q[i].ID]=Ans;
}
go(i,1,t)printf("%d\n",ans[i]);return 0;
}//Paul_Guderian 【例题三】达到顶尖
·述大意:
一棵树,可以单点修改一个节点的权值,许多询问和修改,询问(u,v)表示u到v的路径上,求出最小的没有出现的自然数。
·分析:
带修莫队+树形莫队。要爆炸了。
上文解决了爆炸的带修莫队,如何处理树形莫队?
·树形莫队引入的第一个难点是:如何分块。注意,分块的目的是为了快速访问与查找(例如上文在分析l指针时间复杂度的时候,发现每次最多移动
unit*2次,这就是因为即使是跨越了块,这两个块的相邻关系使得时间复杂度不会改变)。
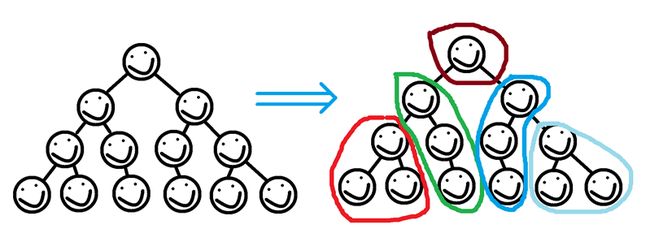
·尝试在树上构造相邻的块,使得:块内元素的互相访问的移动次数控制在一个范围内(也就是unit)。做法是用栈维护当前节点作为父节点访问它的子节点,当从栈顶到父节点的距离大于unit时,弹出这部分元素分为一块。
如图:
(另外,对于剩余分块的节点,也就是根节点附近由于个数小于unit而形成的一坨点,最后再分一块或加在最后一块中)
·强调这样做的好处:使得每一个块内的点到达另一个点最多移动unit次。
那么对于sort()就和第二题一样了。
·接下来还有一个区间移动(即指针u,v,T的移动)没有处理。很明显,这道题的树上路径的维护又是一个美妙的东西。与上几道题不同的是,u,v指针是在树上移动。如果当前路径(u,v)已处理好,下一个询问是到达(u1,v1).那么我们可以将u一步一步的移动到u1,一路上我们欢声笑语,走一个点就记录上面的自然数使用vis[u]标记这个节点来没来过,使用抑或就可以轻松求出访问状态,v到v1也可以这样做。
另外,维护当前已收集的自然数,可以用离散化+数据结构。(但是这道题好像有BUG,不需要离散化)。给出的代码用的方法是用分块维护,但事后想想,发现树状数组可能更美妙。
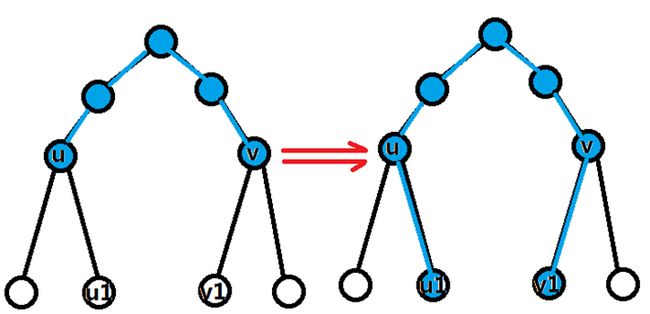
·这一切都得到解决,就在代码要到来时,你偷看了代码,发现里面有一个函数叫做LCA!什么,哪里要用到倍增求公共祖先?一张图如下:
·这样的问题在什么点出现?u1,v1的最近公共祖先。所以,我们上文维护自然数的数据结构(u,v)改成:表示u到v路径上除开他们的LCA的其他点的信息,每次u,v归位后,我们单独为LCA计算一次,这样既避免了怪异情况影响答案,有保证了LCA对答案的贡献。
·网上对这种路径问题还有一种本质相同出发点不同的妙解,它也能帮助理解为什么会有怪异情况:求出该树的欧拉序(类似于dfs序,但每个点有头有尾),那么对于(u,v)路径,就是在序列中仅出现一次的数字。这样做同样也要处理公共祖先卡机的怪异情况,画图看看吧。
·终于出场的大米饼代码:
#include
#include
#include
#define go(i,a,b) for(int i=a;i<=b;i++)
#define ro(i,a,b) for(int i=a;i>=b;i--)
#define fo(i,a,x) for(int i=a[x],v=e[i].v;i;i=e[i].next,v=e[i].v)
using namespace std;const int N=50009;
struct E{int v,next;}e[N*3];
int k=1,head[N],unit,Be[N],m,st[N],top,fa[N][18],deep[N];
int n,Q,a[N],t[N],op,x,y,p,tim,u=1,v=1,T,ans[N],vis[N];
void ADD(int u,int v){e[k]=(E){v,head[u]};head[u]=k++;}
void dfs(int u){
go(i,1,19)if((1<deep[u])break;
else fa[u][i]=fa[fa[u][i-1]][i-1];
int bottom=top;
fo(i,head,u)if(v!=fa[u][0])
{
fa[v][0]=u;deep[v]=deep[u]+1;dfs(v);
if(top-bottom>=unit){m++;while(top!=bottom)Be[st[top--]]=m;}
}
st[++top]=u;
}
int LCA(int x,int y)
{
if(deep[x]deep[y])Run(x),x=fa[x][0];
while(x!=y)Run(x),Run(y),x=fa[x][0],y=fa[y][0];
}
void Mo()
{
go(i,1,p)
{
while(Tq[i].tim)revise(cq[T].u,cq[T].Old),T--;
if(u!=q[i].u)move(u,q[i].u),u=q[i].u;
if(v!=q[i].v)move(v,q[i].v),v=q[i].v;
int anc=LCA(u,v);Run(anc);ans[q[i].id]=Data.mex()-1;Run(anc);
}
}
int main(){scanf("%d%d",&n,&Q);unit=pow(n,0.45);
go(i,1,n)scanf("%d",&a[i]),t[i]=++a[i];
go(i,2,n){int uu,vv;scanf("%d%d",&uu,&vv);ADD(uu,vv);ADD(vv,uu);}
dfs(1);while(top)Be[st[top--]]=m;
go(i,1,Q)
{
scanf("%d%d%d",&op,&x,&y);
if( op)p++,q[p]=(Query){x,y,tim,p};
if(!op)tim++,cq[tim]=(Change){x,y+1,t[x]},t[x]=y+1;
}
Data.n=n+1;Data.init();sort(q+1,q+1+p);Mo();
go(i,1,p)printf("%d\n",ans[i]);
}//Paul_Guderian [小小总结]
莫队算法适用条件是比较苛刻的吗?是的。
①题目必须离线
②能够以极少的时间推出旁边区间(一般是O(1))
③没有修改或者修改不太苛刻
④基于分块,分块不行,它也好不了哪里去(何况现在还有可持久化数据结构维护的分块)
但莫队的思想美妙,代码优美,你值得拥有。莫队的排序思想也为众多离线处理的题目提供了完整的思路。
问题:有n个数组成一个序列,有m个形如询问L, R的询问,每次询问需要回答区间内至少出现2次的数有哪些。
朴素的解法需要读取O(nm)次数。如果数据范围小,可以用数组,时间复杂度为O(nm)。如果使用STL的Map来保存出现的次数,则需要O(nmlogn)的复杂度。有没有更快的方法呢?
注意到询问并没有强制在线,因此我们可以使用离线方法。注意到一点,如果我们有计算完[L, R]时的“中间变量”(在本题为每个数出现的次数),那么[L - 1, R]、[L + 1, R]、[L, R - 1]、[L, R + 1]都能够在“中间变量”的“基本操作时间复杂度”(1)得出。如果能安排适当的询问顺序,使得每次询问都能用上上次运行产生的中间变量,那么我们将可以在更优的复杂度完成整个询问。
(1) 如果数据较小,用数组,时间复杂度为O(1);如果数据较大,可以考虑用离散化或map,时间复杂度为O(logn)。
那如何安排询问呢?这里有个时间复杂度非常优秀的方法:首先将每个询问视为一个“点”,两个点P1, P2之间的距离为abs(L1 - L2) + abs(R1 - R2),即曼哈顿距离,然后求这些点的最小生成树,然后沿着树边遍历一次。由于这里的距离是曼哈顿距离,所以这样的生成树被称为“曼哈顿最小生成树”。最小曼哈顿生成树有专用的算法(2),求生成树时间复杂度可以仅为O(mlogm)。
(2) 其实这里是建边的算法,建边后依然使用传统的Prim或者Kruskal算法来求最小生成树。
不幸的是,曼哈顿最小生成树的写法很复杂,考场上不建议这样做。
一种直观的办法是按照左端点排序,再按照右端点排序。但是这样的表现不好。特别是面对精心设计的数据,这样方法表现得很差。
举个例子,有6个询问如下:(1, 100), (2, 2), (3, 99), (4, 4), (5, 102), (6, 7)。
这个数据已经按照左端点排序了。用上述方法处理时,左端点会移动6次,右端点会移动移动98+97+95+98+95=483次。右端点大幅度地来回移动,严重影响了时间复杂度——排序的复杂度是O(mlogm),所有左端点移动次数仅为为O(n),但右端点每个询问移动O(n),共有m个询问,故总移动次数为O(nm),移动总数为O(mlogm + nm)。运行时间上界并没有减少。
其实我们稍微改变一下询问处理的顺序就能做得更好:(2, 2), (4, 4), (6, 7), (5, 102), (3, 99), (1, 100)。
左端点移动次数为2+2+1+2+2=9次,比原来稍多。右端点移动次数为2+3+95+3+1=104,右端点的移动次数大大降低了。
上面的过程启发我们:①我们不应该严格按照升序排序,而是根据需要灵活一点的排序方法;②如果适当减少右端点移动次数,即使稍微增多一点左端点移动次数,在总的复杂度上看,也是划算的。
在排序时,我们并不是按照左右端点严格升序排序询问,而只是令其左右端点处于“大概是升序”的状态。具体的方法是,把所有的区间划分为不同的块,将每个询问按照左端点的所在块序号排序,左端点块一样则按照右端点排序。注意这个与上一个版本的不同之处在于“第一关键字”是左端点所在块而非左端点。
(3) 由于莫涛经常打比赛做队长,大家都叫他莫队,该算法也被称为莫队算法。(感谢汝佳大神、莫队的指出)
莫队算法首先将整个序列分成√n个块(同样,只是概念上分的块,实际上我们并不需要严格存储块),接着将每个询问按照块序号排序(一样则按照右端点排序)。之后,我们从排序后第一个询问开始,逐个计算答案。
int len; // 块长度
struct Query{
int L, R, ID, block;
Query(){} // 构造函数重载
Query(int l, int r, int ID):L(l), R(r), ID(ID){
block = l / len;
}
bool operator < (const Query rhs) const {
if(block == rhs.block) return R < rhs.R; // 不是if(L == rhs.L) return R < rhs.R; return L < rhs.L
return block < rhs.block; // 否则这就变回算法一了
}
}queries[maxm];
map buf;
inline void insert(int n){
if(buf.count(n))
++buf[n];
else
buf[n] = 1;
}
inline void erase(int n){
if(--buf[n] == 0) buf.erase(n);
}
int A[maxn]; // 原序列
queue anss[maxm]; // 存储答案
int main(){
int n, m;
cin >> n;
len = (int)sqrt(n); // 块长度
for(int i = 1; i <= n; i++){
cin >> A[i];
}
cin >> m;
for(int i = 1; i <= m; i++){
int l, r;
cin >> l >> r;
queries[i] = Query(l, r, i);
}
sort(queries + 1, queries + m + 1);
int L = 1, R = 1;
buf[A[1]] = 1;
for(int i = 1; i <= m; i++){
queue& ans = anss[queries[i].ID];
Query &qi = queries[i];
while(R < qi.R) insert(A[++R]);
while(L > qi.L) insert(A[--L]);
while(R > qi.R) erase(A[R--]);
while(L < qi.L) erase(A[L++]);
for(map::iterator it = buf.begin(); it != buf.end(); ++it){
if(it->second >= 2){
ans.push(it->first);
}
}
}
for(int i = 1; i <= m; i++){
queue& ans = anss[i];
while(!ans.empty()){
cout << ans.front() << ' ';
ans.pop();
}
cout << endl;
}
} 尽管分了块,但是我们可以对所有的“询问转移”一视同仁。上述的代码有几个需要注意的地方。
一是insert和erase,这里在插入前判断了是否存在、插入后判断是否为0,但这不是必须的(insert时会将新节点初始化为0,erase为0后对处理答案不影响);
二是区间变化的顺序,insert最好放在前面,erase最好在后面(想一想,为什么);
三是insert总是使用前缀自增自减运算符,erase总是用后缀运算符;
四是我们在访问我们在“询问转移”前声明了Query的引用,来减少运行时寻址的计算量;
五是我们重载了Query的构造函数。为什么要重载呢?
我们希望在Query得到L, R, ID时自动计算块block,这就要写一个构造函数Query(int L, int R, int ID)来实现。但是,当结构体没有构造函数,实例化时不会初始化,有构造函数则一定会调用构造函数进行初始化。“托他的福”,queries数组建立时会对每个元素调用一次构造函数。可是我们只有有3个参数的构造函数,构造时一定要有3个参数。而建立数组时却没有参数,编译器会报错。折中的办法是写一个没有参数的构造函数,可以避免这一问题。
这样排序有个特点。L和R都是“大概是升序”。不过L大概像爬山,总体上升但是会有局部的小幅度下降。R则有些难以形容,大概可以看出其由很多段快速上升,每段上升到顶端后下降到最底。
下面是随机生成100个数据,将数据放到WPS表格后制成图表后的样子。
还有一个问题,为什么分块要分成√n块呢?我们分析一下时间复杂度。
假设我们每k个点分一块。
如果当前询问与上一询问左端点处在同一块,那么左端点移动为O(k)。虽然右端点移动可能高达O(n),但是整一块询问的右端点移动距离之和也是O(n)(想一想,为什么)。因此平摊意义下,整块移动为O(k) × O(k) + O(n),一共有n / k块,时间复杂度为O(kn + n2 / k)。
如果询问与上一询问左端点不处于同一块,那么左端点移动为O(k),但右端点移动则高达O(n)。幸运的是,这种情况只有O(n / k)个,时间复杂度为O(n + n2 / k)。
总的移动次数为O(kn + n2 / k)。因此,当k = √n时,运行时间上界最优,为O( n1.5 )。
最后,因此根据每次insert和erase的时间复杂度,乘上O(1)或者O(logn)亦或O(n)不等,得到完整算法的时间复杂度(代码使用了map,为O( logn ))。
真的不太理解,其中的分块,待修莫队的时间指针。大体整理了一下,找了两篇思路顺畅的博文先整理存下来。