A Pareto-Efficient Algorithm for Multiple Objective Optimization in E-Commerce Recommendation阅读翻译

备注：大部分通过百度翻译的中文

ABSTRACT 摘要

Recommendation with multiple objectives is an important but difficult problem, where the coherent difficulty lies in the possible conflicts between objectives. In this case, multi-objective optimization is expected to be Pareto efficient, where no single objective can be further improved without hurting the others. However existing approaches to Pareto efficient multi-objective recommendation still lack good theoretical guarantees.
In this paper, we propose a general framework for generating Pareto efficient recommendations. Assuming that there are formal differentiable formulations for the objectives, we coordinate these objectives with a weighted aggregation. Then we propose a condition ensuring Pareto efficiency theoretically and a two-step Pareto efficient optimization algorithm. Meanwhile the algorithm can be easily adapted for Pareto Frontier generation and fair recommendation selection. We specifically apply the proposed framework on E-Commerce recommendation to optimize GMV and CTR simultaneously. Extensive online and offline experiments are conducted on the real-world E-Commerce recommender system and the results validate the Pareto efficiency of the framework.
To the best of our knowledge, this work is among the first to provide a Pareto efficient framework for multi-objective recommendation with theoretical guarantees. Moreover, the framework can be applied to any other objectives with differentiable formulations and any model with gradients, which shows its strong scalability.

多目标推荐是一个重要而困难的问题，其难点在于目标之间可能存在冲突。在这种情况下，我们期望多目标优化是帕累托有效的，即，其中没有一个目标可以在不伤害其他目标的情况下得到进一步的改进。然而，现有的帕累托有效多目标推荐方法仍然缺乏很好的理论保证。

本文提出了一个产生帕累托有效推荐的一般框架。假设目标有形式可微的公式，我们用加权集合来协调这些目标。然后从理论上提出了保证Pareto有效的条件和两步Pareto有效优化算法。同时，该算法可以很好地适应Pareto边界的生成和公平的推荐选择。我们把所提出的框架应用到电子商务推荐来同时优化GMV和CTR。在实际的电子商务推荐系统上进行了大量的在线和离线实验，实验结果验证了该框架的帕累托效率。

据我们所知，这项工作是第一个为多目标推荐提供帕累托有效框架并提供理论保证的工作。此外，该框架还可以应用于任何其他具有可微公式的目标和任何具有梯度的模型，具有很强的可扩展性。

1 INTRODUCTION 简介

Recommender systems are emerging as a crucial role in online services and platforms, which prevent users from information overload. The recommendation algorithms (for example Learning To Rank) generate personalized rankings of items and the top-ranked items are recommended to users. Usually, the algorithms need very careful designs to fulfill multiple objectives. However, it is difficult to optimize multiple objectives simultaneously, where the core difficulty lies in the conflicts between different objectives. In E-Commerce recommendation, CTR (Click Through Rate) and GMV (Gross Merchandise Volume) are two important objectives that are not entirely consistent. To validate this inconsistency, we collect one-week online data from a real-world E-Commerce platform and plot the trends of GMV when CTR . According to the trends reflected in Fig. 1, CTR is not entirely consistent with GMV , and a CTR-optimal or GMV-optimal recommendation can be rather sub-optimal or even bad in terms of the other objective.
推荐系统在网络服务和平台中扮演着重要的角色，它可以防止用户的信息过载。推荐算法（例如排序学习LTR）生成个性化的物品排名，排名靠前的物品推荐给用户。通常，算法需要非常仔细的设计来实现多个目标。但同时优化多个目标是困难的，其核心难点在于不同目标之间存在冲突。在电子商务推荐中，点击率CTR和成交总额GMV是两个不完全一致的重要目标。为了验证这种不一致性，我们从一个真实的电子商务平台收集了一周的在线数据，并绘制了按CTR排序时GMV的趋势图。根据图1所示的趋势，CTR与GMV并不完全一致，就另一个目标而言，按CTR最优或GMV最优进行推荐可能是相当次优的，甚至是不好的。

Therefore, a solution is considered as optimal for two objectives in the sense that no objective can be further improved without hurting the other one. This optimality is widely acknowledged in multiple objective optimization and named as Pareto efficiency or Pareto optimality. In the context of Pareto efficiency, solution A is considered to dominate solution B only when A outperforms B on all the objectives. And the aim of Pareto efficiency is to find solutions that are not dominated by any others.
因此，如果没有一个目标可以在不伤害另一个目标的情况下得到进一步的改进，那么这个解被认为是两个目标的最优解。这种最优性在多目标优化中得到了广泛的认可，被称为帕累托效率或帕累托最优性。在帕累托效率的背景下，只有当A在所有目标上都优于B时，才认为A方案优于B方案。帕累托效率的目标是找到最优的解决方案。

Existing approaches for Pareto optimization can be categorized into two categories: heuristic search and scalarization. Evolutionary algorithms are popular choices in heuristic search approaches. However, heuristic search can not guarantee Pareto efficiency, it only ensures the resulting solutions are not dominated by each other (but still can be dominated by the Pareto efficient solutions) [45]. Unlike heuristic search, scalarization transforms multiple objectives into a single one with a weighted sum of all the objective functions. With proper scalarization, the Pareto efficient solutions can be achieved by optimizing the reformulated objective function. However, the scalarization weights of objective functions are usually determined manually and Pareto efficiency is still not guaranteed. To summarize, it is very difficult for existing evolutionary algorithms and scalarization algorithms to find Pareto efficient solutions with a guarantee. Recently, it is pointed out that the Karush-Kuhn-Tucker (KKT) conditions can be used to guide the scalarization [11]. We build our algorithm upon the KKT conditions and propose a novel algorithmic framework that generates the scalarization weights with theoretical guarantees.
现有的帕累托优化方法可分为两类：启发式搜索和标量化。进化算法是启发式搜索方法中的常用选择。然而，启发式搜索不能保证Pareto有效性，它只能保证得到的解在搜索到的解中最优（但仍然可能不如Pareto有效解）[45]。与启发式搜索不同，标量化将多个目标转换为一个单一的目标，并对所有目标函数进行加权和。在适当的尺度化条件下，通过优化目标函数可以得到Pareto有效解。然而，目标函数的标量化权值通常由人工确定，帕累托效率仍然得不到保证。综上所述，现有的进化算法和标量化算法很难找到具有保证的帕累托有效解。最近，有人指出Karush-Kuhn-Tucker（KKT）条件可以用来指导标度化[11]。我们在KKT条件下建立了算法，并提出了一种新的算法框架，该框架在理论上保证了量化权重的生成。

Specifically, we propose a Pareto-Efficient algorithmic framework “PE-LTR” that optimizes multiple objectives with an LTR procedure. Given the candidate items generated for each user, PE-LTR ranks the candidates so that the ranking is Pareto efficient with respect to multiple objectives. Assuming that there exist differentiable formulations for each objective correspondingly, we adopt the scalarization technique to coordinate different objectives into a single objective function. As stated before, the scalarization technique can not guarantee Pareto efficiency unless the weights are carefully chosen. Therefore, we first propose a condition for the scalarization weights that ensures the solution is Pareto efficient. The condition is equivalent to a constrained optimization problem, and we propose an algorithm that solves the problem in two steps. First we simplify the problem by relaxing the constraints so that an analytic solution is achieved; then we get the feasible solution by conducting a projection procedure. With PE-LTR as the cornerstone, we provide methods to generate the Pareto Frontier and a specific recommendation, depending on the needs of service providers. To generate the Pareto Frontier, one can run PE-LTR by evenly set the bounds of the objective scalarization weights. To generate a specific recommendation, one can either run PE-LTR once with proper bounds or generate the Pareto Frontier first and choose a “fair” solution with specific fairness metric.
具体地说，我们提出了一个帕累托有效的算法框架“PE-LTR”，用LTR过程优化多个目标。给定为每个用户生成的候选项，PE-LTR对候选项进行排序，以便对多个目标进行帕累托有效排序。假设每个目标都有相应的可微公式，采用标量化技术将不同目标协调成一个目标函数。如前所述，除非仔细选择权重，否则标量化技术不能保证帕累托效率。因此，我们首先提出了一个可确保解是帕累托有效的尺度化权重的条件。该条件等价于一个约束优化问题，提出了一种分两步求解的算法。首先通过放松约束使问题简化，得到解析解；然后通过投影过程得到可行解。以PE-LTR为基础，根据服务提供商的需求，我们提供了生成Pareto边界的方法和具体的建议。要生成Pareto边界，可以通过均匀设置目标尺度化权重的边界来运行PE-LTR。为了产生一个特定的推荐，他们可以使用适当的边界运行一次PE-LTR，或者首先生成Pareto边界，然后选择一个具有特定公平度量的“公平”解决方案。

In this paper we apply this framework to optimize two important objectives for E-Commerce recommendation, i.e. GMV and CTR. For E-Commerce platforms, the primary objective is to improve the GMV, but too much sacrifice of CTR may cause a severe decrease of daily active users (DAU) in the long term. Therefore we aim to find Pareto efficient solutions with respect to both objectives. We propose two differentiable formulations for GMV and CTR respectively and apply the PE-LTR framework for generating Pareto-optimal solutions. We conduct extensive experiments on a real-world E-Commerce recommender system and compare the results with state-of-the-art approaches. The online and offline experimental results both indicate that our solution outperforms other baselines significantly and the solutions are nearly Pareto efficient.
本文应用该框架对电子商务推荐的两个重要目标GMV和CTR进行了优化。对于电子商务平台来说，首要的目标是提高GMV，但长期来看，过度舍弃CTR可能会导致日常活跃用户（DAU）的严重减少。因此，我们的目的是找到关于这两个目标的Pareto有效解。我们分别提出了GMV和CTR的两个可微公式，并应用PE-LTR框架生成帕累托最优解。我们在一个真实的电子商务推荐系统上进行了大量的实验，并将结果与最新的方法进行了比较。离线和在线实验结果均表明，我们的解明显优于其他基线，且解接近帕累托效率。

The contributions of this work are:

• We propose a general Pareto efficient algorithmic framework
  (PE-LTR) for multi-objective recommendation. The framework is both model and objective agnostic, which shows its great scalability.
• We propose a two-step algorithm which theoretically guarantees the Pareto efficiency. Despite the algorithm is built upon scalarization technique, it differs from other scalarization approaches with its theoretical guarantee and its automatic learning of scalarization weights rather than manually assignment.
• With PE-LTR as the cornerstone, we present how to generate the Pareto Frontier and a specific recommendation. Specifically, we propose to select a fair recommendation from the Pareto Frontier with proper fairness metrics.
• We use E-Commerce recommendation as a specification of PE-LTR, and conduct extensive online and offline experiments on a real-world recommender system. The results indicate that our algorithm outperforms other state-of-the-art approaches significantly and the solutions generated are Pareto efficient.
• We open-source a large-scale E-Commerce recommendation dataset EC-REC, which contains the real records of impressions, clicks and purchases. To the best of our knowledge, no public dataset includes all three labels and enough features, this dataset can be used for further studies.
  这项工作的贡献是：
• 我们提出了一个通用的帕累托有效算法框架（PE-LTR）用于多目标推荐。该框架既不依赖于模型，也不依赖于目标，显示了其强大的可伸缩性。
• 我们提出一个两步算法，从理论上保证帕累托效率。尽管该算法是建立在标量化技术的基础上的，但它不同于其他标量化方法，它具有理论保证和标量化权值的自动学习，而不是手工赋值。
• 以PE-LTR为基础，我们介绍了如何生成帕累托前沿和具体推荐。具体来说，我们提出从帕累托边界中选择一个公平的推荐，并使用适当的公平度量。
• 我们使用电子商务推荐作为PE-LTR的规范，并在现实世界的推荐系统上进行广泛的在线和离线实验。结果表明，我们的算法明显优于其他最新方法，并且生成的解是帕累托有效的。
• 我们开源了一个大型电子商务推荐数据集EC-REC，其中包含展现、点击和购买的真实记录。据我们所知，这是第一个包含所有三个标签和足够特征的公共数据集，这个数据集可以用于进一步的研究。

2 RELATED WORK 相关工作

In this section, we provide a detailed introduction to the related studies from the following aspects: recommendation with multiple objectives, E-Commerce recommendation and learning to rank.
本部分从多目标推荐、电子商务推荐、排序学习等方面对相关研究进行了详细介绍。

2.1 Recommendation with Multiple Objectives 多目标推荐

We look at the studies on multi-objective recommendation from two aspects, i.e. the objectives concerned and the approaches for multi-objective recommendations.
Despite the recommendation accuracy is the main concern, some studies argue that other characteristics such as the availability, profitability, or usefulness should be considered simultaneously [15, 22]. Some studies attempt to model the trade-off s between relevance and diversity in recommendation [14, 17, 41]. When multiple objectives are concerned, it is expected to get a Pareto efficient recommendation [27, 28]. Recently, it is pointed out that some multiple objectives are related to users [7, 16, 23, 29]. On one hand, different objectives are related to different user behaviors. For example, both clicks and hides are considered in LinkedIn feeds [33]. On the other hand, the objectives are related to different user statuses, for example different stakeholders [8, 23].
本文从多目标推荐的目标和方法两个方面对多目标推荐进行了研究。

尽管推荐的准确性是主要问题，但一些研究认为，其他特征，如可用性、盈利能力或有用性，应同时考虑[15，22]。一些研究试图在推荐[14、17、41]中对相关性和多样性之间的权衡进行建模。当涉及多个目标时，期望得到帕累托有效的推荐[27，28]。最近有人指出，有些多目标与用户有关[7、16、23、29]。一方面，不同的目标与不同的用户行为有关。例如，在LinkedIn订阅源[33]中，点击和隐藏都被考虑在内。另一方面，目标与不同的用户状态相关，例如不同的涉众[8，23]。

The approaches on recommendation with multiple objectives can be categorized into evolutionary algorithm [45] and scalarization [38]. The evolutionary algorithm has been used for long- tail recommendation [35], diversified recommendation [10], and novelty-aware recommendation [28]. And it has also been used for Pareto efficient hybridization [28] of multiple recommendation algorithms. Scalarization technique is also used for recommendation with multiple objectives [38]. However, existing studies mostly depend on manually assigned weights for scalarization, whose Pareto efficiency can not be guaranteed. Recently, the KKT conditions are used for guiding scalarization techniques [11, 32]. However, existing algorithms based on these conditions are limited to the unconstrained cases and can not t the requirements in real-world scenarios.
多目标推荐方法可分为进化算法[45]和标量化[38]。进化算法已用于长尾推荐[35]、多样化推荐[10]和新颖性感知推荐[28]。它也被用于多重推荐算法的帕累托有效混合[28]。标量化技术也用于多目标推荐[38]。然而，现有的研究大多是针对手工赋权的标量化问题，其帕累托效率不能得到保证。最近，KKT条件被用来指导标量化技术[11，32]。然而，现有的基于这些条件的算法仅限于无约束情况，不能满足真实场景中的要求。

2.2 E-Commerce Recommendation 电子商务推荐

E-Commerce recommendation is also a popular research topic. Some studies adopt economic theory models and Markov chains for recommendation [12, 19, 42, 43]. While some other studies focus on other aspects in E-Commerce recommendation [1, 30, 34, 40], such as feature learning and diversification. It is pointed out that a good practice in E-Commerce searching is learning to rank [18], which also coincides with the motivation of our framework. Usually there are multiple stages in E-Commerce recommendation, for example clicks and purchases. Therefore the learning-to-rank algorithms need to jointly optimize multiple stages [36]. Some studies focus on the post-click stage in searching and recommendation. For example, the bidding price and revenue are jointly considered with relevance [26, 44]. Recently, two studies focus on the connection between clicks and purchases in E-Commerce searching and advertising [21, 36]. As optimizing clicks and purchases are not entirely consistent, it is necessary to find a Pareto efficient trade-off between them, which is not considered in previous studies on purchase optimization [21, 36].
电子商务推荐也是一个热门的研究课题。一些研究侧重于推荐中的经济理论模型和马尔可夫链[12，19，42，43]。而其他一些研究则侧重于电子商务推荐中的其他方面，如特征学习和多样化。电子商务搜索的一个良好实践是排序学习[18]，这也符合我们框架的动机。电子商务推荐通常有多个阶段，如点击和购买。因此，排序学习算法需要联合优化多个阶段[36]。一些研究集中在搜索和推荐中的点击后阶段。例如，投标价格和收入与相关性一起考虑[26，44]。最近，有两项研究关注电子商务搜索和广告中点击和购买之间的关系[21，36]。由于优化点击和购买并不完全一致，因此有必要在它们之间找到帕累托有效的折衷，这在以往的购买优化研究中是没有考虑到的[21，36]。

2.3 Learning to Rank 排序学习

Learning To Rank (LTR) has been a popular research topic for quite a long time. The studies on LTR can be categorized into point-wise, pair-wise and list-wise approaches. The point-wise scheme [20] predicts the individual instance separately; the pair-wise scheme [4, 13] is approximated as a binary classification problem, which focuses on the relative order of a pair of instances; while the list-wise scheme [5, 6, 37, 39] directly optimizes the metric of a ranking list. Usually, list-wise LTR achieves superior performances than other schemes.
ranking methods have been proposed, such as RankNet [4], Rank- Boost [13], AdaRank [39], LambdaRank [5], ListNet [6] and LambdaMART [37]. Due to the similarity between searching and recommendation in ranking, LTR approaches are widely used in both scenarios. Recently, it is pointed out that LTR is a key component in E-Commerce searching [18], which is able to exploit multiple user feedback signals for relevance modeling, including clicks, add-to-cart ratios, and revenue.
According to the previous studies, LambdaMART is one of the best performing algorithms [36]. As focus of this paper is not about ranking model, we choose a simple point-wise ranking model for the proposed framework.
长期以来，排序学习一直是一个热门的研究课题。LTR的研究可分为point-wise、pair-wise和list-wise。point-wise方案[20]分别预测个体实例；pair-wise方案[4, 13]被近似为二分类问题，其集中于一对实例的相对顺序；而list-wise方案[5, 6, 37，39]直接优化排序列表的度量。通常，list-wise LTR比其他方案具有更好的性能。

目前已有多种排序方法，如RankNet[4]、Rank-Boost[13]、AdaRank[39]、LambdaRank[5]、ListNet[6]和LambdaMART[37]。由于搜索和推荐排序的相似性，LTR方法在这两种情况下都得到了广泛的应用。最近，有人指出LTR是电子商务搜索中的一个关键组件[18]，它能够利用多个用户反馈信号进行相关性建模，包括点击率、购物车添加比率和收入。

根据之前的研究，LambdaMART是性能最好的算法之一[36]。由于本文的研究重点不是排序模型，因此我们选择了一个简单的point-wise排序模型作为框架。

3 PROPOSED FRAMEWORK 提出的框架

In this section, we first provide a brief introduction to the concept of Pareto efficiency. Then we introduce the details of the proposed framework, i.e. Pareto-Efficient Learning-to-Rank (PE-LTR). Assuming that there are differentiable loss functions for multiple objectives correspondingly, we propose a condition that guarantees the Pareto efficiency of the solution. We show that the proposed condition is equivalent to a constrained Quadratic Programming problem. Then we propose a two-step algorithm to solve this problem. Moreover, we provide methods to generate both Pareto Frontier and specific single recommendation with PE-LTR.
在这一节中，我们首先简要介绍帕累托效率的概念。然后详细介绍了该框架，即Pareto有效学习排序（PE-LTR）。假设多目标对应有可微损失函数，我们提出了保证解的帕累托效率的条件。证明了该条件等价于一个约束二次规划问题。然后我们提出了一个两步算法来解决这个问题。此外，我们还提供了利用PE-LTR生成Pareto前沿和特定单一推荐的方法。

3.1 Preliminary 前言

First, we provide a brief introduction to Pareto efficiency and some related concepts. Pareto efficiency is an important concept in multiple objective optimization. Given a system which aims to minimize a series of objective functions $f_1,...,f_K$ , Pareto efficiency is a state when it is impossible to improve one objective without hurting other objectives in terms of multi-objective optimization.
首先，我们简要介绍了帕累托效率和相关概念。帕累托效率是多目标优化中的一个重要概念。假定一个系统的目标是最小化一系列目标函数 $f_1,...,f_K$，Pareto效率是指在多目标优化中，一个目标不可能在不影响其他目标的情况下得到改善的状态。

Definition 3.1. Denote the outcomes of two solutions as $s_i=(f_1^i,...,f_K^i)$ and $s_j=(f_1^j,...,f_K^j)$, $s_i$ dominates $s_j$ if and only if $f_1^i\le f_1^j,f_2^i\le f_2^j,...,f_K^i\le f_K^j$ (for minimization objectives).
The concept of Pareto efficiency is built upon the definition of domination:
Definition 3.2. A solution $s_i=(f_1^i,...,f_K^i)$ is Pareto efficient if there is no other solution $sj=(f_1^j,...,f_K^j)$ that dominates $s_i$.
Therefore, a solution that is not Pareto efficient can still be improved for at least one objective without hurting the others, and it is always expected to achieve Pareto efficient solutions in multi-objective optimization. It is worth mentioning that Pareto efficient solutions are not unique and the set of all such solutions is named as the “Pareto Frontier”
定义3.1。将两个方案的结果表示为$s_i=(f_1^i,...,f_K^i)$和$s_j=(f_1^j,...,f_K^j)$，当且仅当$f_1^i\le f_1^j,f_2^i\le f_2^j,...,f_K^i\le f_K^j$（用于最小化目标）时，$s_i$ 支配 $s_j$。

帕累托效率的概念建立在支配的定义之上：

定义3.2。一个解$s_i=(f_1^i,...,f_K^i)$是帕累托有效的，如果没有其他解决方案$s_j=(f_1^j,...,f_K^j)$支配$s_i$。

因此，在多目标优化中，一个非帕累托有效解仍然可以在不损害其他目标的情况下至少对一个目标进行改进，并且总是期望能得到帕累托有效解。值得一提的是，Pareto有效解并不是唯一的，所有这些解的集合称为"帕累托边界"。

3.2 Pareto-Efficient Learning to Rank 帕累托有效的排序学习

To achieve a Pareto efficient solution, we propose a Learning-to-Rank scheme that optimizes multiple objectives with the scalarization technique. Assuming that there are K objectives in a given recommender system, a model F(θ) needs to optimize these objectives simultaneously, where θ denotes the model parameters. Without loss of generality, we assume that there exist K differentiable loss functions $L_i(\theta ),\forall i\in 1,...,K$ for the K objectives correspondingly.
为了得到帕累托有效解，我们提出了一个排序学习的方案，利用标量化技术优化多个目标。假设在给定的推荐系统中存在K个目标，则F(θ)模型需要同时优化这些目标，其中θ表示模型参数。在不损失一般性的情况下，我们假设K个目标存在K个可微损失函数$L_i(\theta ),\forall i\in 1,...,K$。

Given the formulations, optimizing i-th objective is equal to minimizing $L_i$ . However, optimizing these K objectives simultaneously is non-trivial, since the optimal solution to one objective is usually sub-optimal for another one. Therefore, we use the scalarization technique to merge multiple objectives into a single one. Specifically, we aggregate the loss functions $L_i$ with ${\omega }_i,\forall i\in 1,...,K$:

$L(\theta )={\sum }_{i=1}^K{w}_i{L}_i(\theta )$

where ${\sum }_{i=1}^K{w}_i=1$ and $\omega i\ge 0,\forall i\in 1,...,K$. In real-world
scenarios, the objectives may have different priorities. In our case, we assume that the constraints added to the objectives are pre-defined boundary constraints, i.e. ${\omega }_i\ge c_i,\forall i\in 1,...,K$, where $c_i$ is a constant between 0 and 1, and ${\sum }_{i=1}^K{c}_i\le 1.$
Despite the single-objective formulation, it is not guaranteed that the solution to the problem is Pareto efficient, unless proper weights are assigned. Then we derive the condition on the scalarization weights that ensures the solution is Pareto efficient.

给定公式，优化第i个目标等于最小化$L_i$。然而，同时优化这些K个目标是很有挑战性的，因为一个目标的最优解通常是另一个目标的次优解。因此，我们使用标量化技术将多个目标合并为一个目标。具体地说，我们把损失函数$L_i$用${\omega }_i,\forall i\in 1,...,K$加起来：

$L(\theta )={\sum }_{i=1}^K{w}_i{L}_i(\theta )$

其中${\sum }_{i=1}^K{w}_i=1$ 并且 $\omega i\ge 0,\forall i\in 1,...,K$。在现实场景中，目标可能有不同的优先级。就我们而言，我们假设在目标中添加的约束是预定义的边界约束，即${\omega }_i\ge c_i,\forall i\in 1,...,K$，其中$c_i$是介于0和1之间的常数，并且${\sum }_{i=1}^K{c}_i\le 1$。

尽管只有一个目标公式，但除非赋予适当的权重，否则不能保证问题的解是帕累托有效的。我们给出了保证解是帕累托有效的标量化权重的条件。

3.2.1 The Pareto Efficient condition. 帕累托有效条件

To get the Pareto efficient solutions for multiple objectives, we attempt to minimize the aggregated loss function. Consider the KKT conditions (Karush-Kuhn-Tucher Conditions) [2] for the model parameters:

$\sum _{i=1}^K{\omega }_i=1,\exists {\omega }_i\ge c_i,i\in 1,...,Kand\sum _{i=1}^K{\omega }_i{\nabla }_{\theta }{L}_i(\theta )=0$

where ${\nabla }_{\theta }{L}_i(\theta )$ is the gradient of $L_i$ . Solutions that satisfy this condition are referred to as Pareto stationary. The condition can be transformed into the following optimization problem:

为了得到多目标的帕累托有效解，我们尝试最小化累加的损失函数。考虑模型参数的KKT条件（Karush-Kuhn-Tucher条件）[2]：

$\sum _{i=1}^K{\omega }_i=1,\exists {\omega }_i\ge c_i,i\in 1,...,Kand\sum _{i=1}^K{\omega }_i{\nabla }_{\theta }{L}_i(\theta )=0$

其中${\nabla }_{\theta }{L}_i(\theta )$ 是$L_i$的梯度。满足此条件的解称为Pareto平稳解。该条件可转化为以下优化问题：

It has been proven [32] that either the solution to this optimization problem is 0 so that the KKT conditions are satisfied or the solutions lead to gradient directions that minimizes all the loss functions. If the KKT conditions are satisfied, the solution is Pareto stationary and also Pareto efficient under realistic and mild conditions [32]. Based on this condition, we propose an algorithmic framework named PE-LTR, whose details are illustrated in Alg. 1.
已经证明了[32]这个优化问题的解要么是0，从而满足KKT条件，要么沿梯度方向，使所有损失函数最小化。如果KKT条件满足，则解是Pareto平稳的，并且在现实和温和条件下也是Pareto有效的[32]。在此基础上，我们提出了一个算法框架PE-LTR，其细节在Alg.1中给出了说明。

The framework starts with uniform scalarization weights and then updates the model parameters and the scalarization weights alternatively. The core part of PE-LTR is the PECsolver, which generates scalarization weights by solving the condition in Problem (1). Note that the condition is a complex Quadratic Programming problem, we present the detailed process of PECsolver in Alg 2.
It is worth mentioning that the algorithmic framework does not rely on specific formulations of the loss functions or the model structures. Any model and formulation with gradients can be easily applied to the framework. Despite the algorithms runs with stochastic gradient descent in batches, the algorithm provides a theoretical guarantee of convergence as gradient descent [11].

该框架从统一的尺度化权重开始，然后交替更新模型参数和尺度化权重。PE-LTR的核心部分是PECsolver，它通过求解问题（1）中的条件来生成标量化权重。注意该条件是一个复杂的二次规划问题，我们在算法2给出了PECsolver的详细过程。
值得一提的是，算法框架并不依赖于损失函数或模型结构的具体公式。任何带有梯度的模型和公式都可以很容易地应用到框架中。尽管算法是批量随机梯度下降的，但该算法提供了梯度下降收敛的理论保证[11]。

3.2.2 The Algorithm for Quadratic Programming 二次规划的算法

Denote ${\hat{w}}_i$ as ${\omega }_i-c_i$ , the Pareto efficient condition becomes:
$min.||\sum _{i=1}^K({\hat{w}}_i+c_i){\nabla }_{\theta }{L}_i(\theta )|{|}_2^2$ （2）
$s.t.\sum _{i=1}^K{\hat{w}}_i=1-\sum _{i=1}^K{c}_i,{\hat{w}}_i\ge 0,\forall i\in 1,...,K$
The Pareto-Efficient condition is equivalent to Problem 1, however, it is not a trivial task to solve this problem due to its quadratic programming form. Therefore, we propose a two-step algorithm as the Pareto efficient condition solver. The algorithm is illustrated in Alg. 2. We first relax the problem by only considering the equality constraints and solve the relaxed problem with an analytical solution. Then we introduce a projection procedure that generates a valid solution from the feasible set with all the constraints.

用${\hat{w}}_i$ 表示 ${\omega }_i-c_i$，帕累托有效条件变为：
$min.||\sum _{i=1}^K({\hat{w}}_i+c_i){\nabla }_{\theta }{L}_i(\theta )|{|}_2^2$                                     （2）
$s.t.\sum _{i=1}^K{\hat{w}}_i=1-\sum _{i=1}^K{c}_i,{\hat{w}}_i\ge 0,\forall i\in 1,...,K$

Pareto有效条件等价于问题1，但由于其二次规划的形式，求解该问题并非易事。因此，我们提出了一个两步算法作为帕累托有效条件求解器。算法在Alg.2 中进行了说明。我们首先通过只考虑等式约束来放松问题，然后用解析解来解决放松问题。然后，我们引入一个投影过程，在所有约束条件下从可行集生成一个有效解。
When all the other constraints are omitted except the equality constraints:
$min.||\sum _{i=1}^K({\hat{w}}_i+c_i){\nabla }_{\theta }{L}_i(\theta )|{|}_2^2$   $s.t.\sum _{i=1}^K{\hat{w}}_i=1-\sum _{i=1}^K{c}_i$         (3)
The solution to the relaxed problem is given by Theorem 3.3.

当忽略除相等约束以外的所有其他约束时：
$min.||\sum _{i=1}^K({\hat{w}}_i+c_i){\nabla }_{\theta }{L}_i(\theta )|{|}_2^2$   $s.t.\sum _{i=1}^K{\hat{w}}_i=1-\sum _{i=1}^K{c}_i$         (3)
松弛问题的解由定理3.3给出。
Theorem 3.3. The solution to the equality constrained problem (3) is given by $\tilde{w}=((M^{T}M{)}^{-1}M\tilde{z})[1:k]$, where $G\in R^{K\times m}$ is the stacking matrix of $\nabla L_i(\theta ),e\in R^K$ is the vector whose elements are all 1,$c\in R^K$ is the concatenated vector of $c_i,\tilde{z}\in R^{K+1}$ is the concatenated vector of $-G{G}^{T}c$ and $1-{\sum }_{i=1}^K{c}_i$, and M is $\left[\begin{array}{cc}G{G}^T& e\\ e^T& 0\end{array}\right]$.
定理3.3。等式约束问题（3）的解由$\tilde{w}=((M^{T}M{)}^{-1}M\tilde{z})[1:k]$给出，其中$G\in R^{K\times m}$是$\nabla L_i(\theta )$的叠加矩阵，$e\in R^K$是所有元素都为1的向量，$c\in R^K$是$c_i$的级联向量，$\tilde{z}\in R^{K+1}$是$-G{G}^{T}c$ 和 $1-{\sum }_{i=1}^K{c}_i$的连接向量，M是$\left[\begin{array}{cc}G{G}^T& e\\ e^T& 0\end{array}\right]$。

The proof to this theorem is in the appendix.
However, the solution ${\hat{w}}^{\ast }$ to problem 3 may not be valid since the non-negativity constraints are omitted. Therefore, we conduct the following projection step to get a valid solution:
$min.||\tilde{w}-\widehat{w^{\ast }}|{|}_2^{2}s.t.\sum _{i=1}^K{\tilde{w}}_i=1,{\tilde{w}}_i\ge 0,\forall i\in$ {1,…,K}      (4)

This problem is exactly a non-negative least squares problem, and can be solved easily with the active set method [3]. Due to 1 page limit, we omit the details of the algorithm to Problem 3 .The complexity of Alg. 2 is mostly determined by the pseudo-inverse operation, which relates to the number of objectives. Usually the number of objectives is limited, therefore the running time of Alg. 2 is negligible and the online experiments have verified this.

这个定理的证明在附录中。
然而，问题3的解${\hat{w}}^{\ast }$可能无效，因为省略了非负性约束。因此，我们执行以下投影步骤以获得有效的解决方案：
$min.||\tilde{w}-\widehat{w^{\ast }}|{|}_2^{2}s.t.\sum _{i=1}^K{\tilde{w}}_i=1,{\tilde{w}}_i\ge 0,\forall i\in$ {1,…,K}      (4)
该问题正是一个非负最小二乘问题，用主动集方法很容易解决[3]。由于1页的限制，我们忽略了问题3算法的细节。Alg.2 的复杂性主要由伪逆运算确定，伪逆运算与目标数目有关。通常目标的数目是有限的，因此Alg.2的运行时间可以忽略不计，在线实验已经证实了这一点。

4 PARETO FRONTIER GENERATION AND SOLUTION SELECTION 帕累托边界生成与解决方案选择

Multiple objective optimization can either be used to find a certain Pareto solution, or be used to generate a set of solutions to construct the Pareto Frontier. In this section, we introduce the details of generating solutions with Alg.1 for the two cases.
多目标优化既可以用来寻找特定的帕累托解，也可以用来生成一组解来构造帕累托边界。在本节中，我们将详细介绍用Alg.1生成这两种解的方法。

4.1 Pareto Frontier Generation 帕累托边界生成

With Alg.1, we can obtain a Pareto optimal solution given the bounds of different objectives. However, there are cases when a series of Pareto optimal solutions are expected, i.e. the Pareto Frontier. This is straight-forward for the algorithmic framework, we can set different values to the bounds of the objectives and perform Alg.1 with different bounds respectively.
To get a Pareto Frontier, we conduct Alg.1 for several times, and the solution generated with proper bound in each run yields a Pareto optimal solution. We choose the bounds properly so that the evenly distributed Pareto points make a good evenly distributed approximation of the Pareto Frontier.
利用Alg.1，我们可以得到给定不同目标边界的帕累托最优解。然而，有时我们期望得到一系列帕累托最优解，即帕累托边界。这对于算法框架来说是很直接的，我们可以为目标的边界设置不同的值，并分别对不同边界执行Alg.1。

为了得到帕累托边界，我们进行了多次Alg.1，每次运行中用适当的边界生成的解得到帕累托最优解。我们适当地选择了边界，使得均匀分布的帕累托点能够很好地均匀地逼近帕累托边界。

4.2 Solution Selection 方案选择

In cases when a single recommendation is expected, we need to select one certain Pareto optimal solution. When the priorities of different objectives are available, we can obtain a proper Pareto-efficient recommendation by setting a proper bound for the objectives and conduct a single run of Alg.1.
如果只期望单一的推荐，我们需要选择一个特定的帕累托最优解。当不同目标的优先级可用时，我们可以通过设置目标的适当界限并运行一次Alg.1来获得适当的帕累托有效推荐。

When the priorities are not available, we can first generate the Pareto Frontier and select a solution that is “fair” for the objectives. There are several definitions of fairness in both economic theories and recommendation system context [38]. One of the most intuitive metrics is Least Misery, which focuses on the most “miserable” objective, in our case, a “Least Misery” recommendation is to minimize the highest loss function of the objectives:

min max $L_1,L_2,...,L_K$ (5)
Another frequently used measure is fairness marginal utility, i.e., to select a solution where the cost of optimizing one objective is almost equal to the benefit of the other objectives:
$min.||\partial (L_1\cdot L_2\cdot ...L_K)/\partial \theta |{|}_2$     (6)
Given the generated Pareto Frontier, the solution with minimum values of Eqn. 5 or Eqn. 6 is selected as the final recommendation, depending on the choice of fairness.

当优先级不可用时，我们可以首先生成帕累托边界，并为目标选择一个“公平”的解决方案。在经济理论和推荐系统场景下，公平有几种定义[38]。最直观的指标之一是最小痛苦，它关注的是最“痛苦”的目标，在我们的案例中，“最小痛苦”的建议是最小化目标的最大损失函数：

min max { $L_1,L_2,...,L_K$} (5)

另一个常用的度量方法是公平边际效用，即选择一个优化目标的成本几乎等于其他目标收益的解决方案：

$min.||\partial (L_1\cdot L_2\cdot ...L_K)/\partial \theta |{|}_2$     (6)

给定生成的帕累托边界，依据公平性，选择有最小值的Eqn.5或Eqn.6作为最终的推荐。

5 SPECIFICATION ON E-COMMERCE RECOMMENDATION 电子商务推荐规范

Given the algorithmic framework of PE-LTR, we introduce the details of its specification on E-Commerce recommendation. Two of the most important objectives in E-Commerce recommendation are GMV and CTR. For E-Commerce platforms, GMV is usually the primary objective. However, CTR is a crucial metric for evaluating user experiences thus affects the scale of the platform in the long term. Therefore, we aim to find a recommendation that is Pareto-Optimal with respect to these two objectives.
在给出PE-LTR算法框架的基础上，我们详细介绍了PE-LTR规范在电子商务推荐中的应用。电子商务推荐的两个最重要的目标是GMV和CTR。对于电子商务平台，GMV通常是首要目标。然而，CTR是评估用户体验的一个重要指标，因此长期影响平台的规模。因此，我们的目标是找到一个关于这两个目标的帕累托最优的推荐。

Considering that in real-life environments, the LTR models take streaming data as input and updates its parameters in an online fashion. Therefore, the online LTR model usually follows the point-wise ranking scheme. We formulate the problem as a binary classification problem and two differentiable loss functions are designed for the two objectives correspondingly.
考虑到在现实环境中，LTR模型以流数据为输入，在线更新其参数。因此，在线LTR模型通常遵循point-wise排序方案。我们将问题描述为二元分类问题，并针对这两个目标分别设计了两个可微损失函数。

In E-Commerce recommender systems, user feedbacks can be roughly categorized into three types: the impressions, the clicks and the purchases. Denote the instances as $(x_j,y_j,z_j),\forall j\in [1,...,N]$, given a point-wise ranking model F(θ), we propose to optimize these two objectives, i.e. CTR and GMV. For CTR optimization, we aim to minimize:
$L_{CTR}(\theta ,x,y,z)=-\frac{1}{N}\sum _{j=1}^{N}log(P(y_j|\theta ,x_j))$
For GMV optimization, we aim to minimize:
$L_{GMV}(\theta ,x,y,z)=-\frac{1}{N}\sum _{j=1}^{N}h(pric{e}_j).log(P(z_j=1|\theta ,x_j))$
$=-\frac{1}{N}\sum _{j=1}^{N}h(pric{e}_j).(log(P(y_j=1|\theta ,x_j))+log(P(z_j=1|y_j=1)))$
$=-\frac{1}{N}\sum _{j=1}^{N}h(pric{e}_j).(log(P(y_j=1|\theta ,x_j)))+g(pric{e}_j)h(pric{e}_j)$

where $h(pric{e}_j)$ is a concave monotone non-decreasing function with respect to $pric{e}_j$, $pric{e}_j$ denotes the price of the item in $x_j$ . In our formulation, we choose $h(pric{e}_j)=log(pric{e}_j)$. And we assume $P(z_j=1|y_j=1)$ is irrelevant of the model parameters θ. Therefore, given a model F(θ) and the formulation of $L_{CTR}(\theta ,x,y,z)$ and $L_{GMV}(\theta ,x,y,z)$, the E-Commerce recommendation problem becomes:
$min.\{L_{CTR}(\theta ,x,y,z),L_{GMV}(\theta ,x,y,z)\}s.t.\theta \in R^m$

在电子商务推荐系统中，用户反馈大致可以分为三类：印象反馈、点击反馈和购买反馈。将实例表示为$(x_j,y_j,z_j),\forall j\in [1,...,N]$，给定一个point-wise排序模型F(θ)，我们提出优化这两个目标，即CTR和GMV。对于CTR优化，我们的目标是最小化：
$L_{CTR}(\theta ,x,y,z)=-\frac{1}{N}\sum _{j=1}^{N}log(P(y_j|\theta ,x_j))$
对于GMV优化，我们的目标是最小化：
$L_{GMV}(\theta ,x,y,z)=-\frac{1}{N}\sum _{j=1}^{N}h(pric{e}_j).log(P(z_j=1|\theta ,x_j))$
$=-\frac{1}{N}\sum _{j=1}^{N}h(pric{e}_j).(log(P(y_j=1|\theta ,x_j))+log(P(z_j=1|y_j=1)))$
$=-\frac{1}{N}\sum _{j=1}^{N}h(pric{e}_j).(log(P(y_j=1|\theta ,x_j)))+g(pric{e}_j)h(pric{e}_j)$

其中$h(pric{e}_j)$是关于$pric{e}_j$的凹单调非递减函数，$pric{e}_j$表示$x_j$中项目的价格。在我们的公式中，我们选择$h(pric{e}_j)=log(pric{e}_j)$。假设$P(z_j=1|y_j=1)$与模型参数θ无关。因此，给定模型F(θ)和$L_{CTR}(\theta ,x,y,z)$ 以及 $L_{GMV}(\theta ,x,y,z)$的表达式，电子商务推荐问题变成：
$min.\{L_{CTR}(\theta ,x,y,z),L_{GMV}(\theta ,x,y,z)\}s.t.\theta \in R^m$

Note that the proposed framework does not rely on specific model structure or the formulations of the losses, it works as long as the model has gradients. Thus the formulations of CTR and GMV losses are not the focus of this paper, and more carefully designed formulations can be accommodated into this framework. Meanwhile we do not focus on a specific LTR model but use three different typical models for comparison, i.e. Logistic Regression (LR), Deep Neural Network (DNN) and Wide&Deep (WDL). The DNN model is a three-layer MLP and has a same structure with the deep component in the Wide&Deep model. For all the neural network components, we choose tanh as the activation function for each hidden layer while the final layer employs the linear function as the output. The comparison between three different models is illustrated in Fig 5 in the experiments.
注意，提议的框架不依赖于特定模型结构或损失公式，只要模型有梯度，它就可以工作。因此，CTR和GMV损失的计算公式不是本文的重点，可以在这个框架中容纳更为精心设计的计算公式。同时，我们不关注特定的LTR模型，而是使用三种不同的典型模型进行比较，即逻辑回归（LR）、深度神经网络（DNN）和Wide&Deep（WDL）。DNN模型是一个三层MLP模型，其结构与Wide&Deep模型中的深部分组件相同。对于所有的神经网络组件，我们选择tanh作为每个隐藏层的激活函数，而最后一层使用线性函数作为输出。实验中三种不同模型的比较如图5所示。

6 EXPERIMENTS 实验

In this section, we introduce the details of experiments which are designed to answer the following research questions:
• How does the framework perform in comparison with state-of-the-art CTR/GMV oriented approaches and multiple objective recommendation algorithms?
• How is the Pareto efficiency of the proposed framework in terms of the single recommendation and Pareto Frontier?
• How is the scalability of the proposed framework in terms of model selection?
To answer these research questions, we conduct extensive experiments on real-world datasets on a popular E-Commerce website, including online and offline experiments.

在本节中，我们将介绍旨在回答以下研究问题的实验细节：
•与目前最先进的面向CTR/GMV的方法和多目标推荐算法相比，框架的性能如何？
•就单一推荐和帕累托边界而言，所提框架的帕累托效率如何？
•所提框架在模型选择方面的可扩展性如何？

为了回答这些研究问题，我们在一个流行的电子商务网站上对真实数据进行了广泛的实验，包括在线和离线实验。

6.1 Datasets 数据集

To the best of our knowledge, there is no publicly available E-Commerce dataset that contains important features such as price and the labels of impression, click and purchase at the same time. Therefore, we collect a real-world dataset EC-REC from a popular E-Commerce platform. Due to the huge amount of online data, we collect one-week data and sample over seven million impressions for offline experiments, and the dataset will be released to the public to support future studies. Meanwhile, we use PE-LTR to serve the users and conduct A/B test for online experiments. The features are from the user profiles and item profiles, for example the purchasing power of users and the average number of purchases of items.

据我们所知，目前还没有同时包含价格和展现、点击、购买label等重要特征的电子商务数据集。因此，我们从一个流行的电子商务平台收集了一个真实的数据集EC-REC。由于在线数据量巨大，我们收集了一周的数据，并为离线实验采集了超过700万条展现数据，数据集将向公众发布，以支持未来的研究。同时，利用PE-LTR为用户服务，对在线实验进行A/B测试。这些特征来自user profile和item profile，例如用户的购买力和物品的平均购买次数。

6.2 Experimental Settings 实验设置

We conduct both offline and online experiments to validate the effectiveness of the proposed framework. state-of-the-art approaches are selected for comparison.
我们进行了离线和在线实验来验证所提框架的有效性。选择最先进的方法进行比较。

6.2.1 Baselines. 基线

We select the state-of-the-art recommendation approaches for comparison and the baselines can be categorized into the three kinds: the typical approaches (CF, LambdaMART), the GMV-oriented approaches (LETORIF, MTL-REC), and the approaches that optimize both objectives (CXR-RL, PO-EA).
我们选择最新的推荐方法进行比较，基线可以分为三类：典型方法（CF、LambdaMART）、面向GMV的方法（LETORIF、MTL-REC）和优化两个目标的方法（CXR-RL、PO-EA）。

• ItemCF: Item-based Collaborative Filtering [31].

• LambdaMART [37] is a state-of-the-art learning-to-rank approach. A MART model is used to optimize a differentiable loss for NDCG. However, LambdaMART only concerns with clicks relevance, while purchase is not considered.

• LETORIF [36] is a recent learning-to-rank approach for GMV maximization and adopts priceCTRCVR for ranking, where CTR and CVR are predictions from the two separate models.

• MTL-REC: MTL-REC [21] adopts multi-task learning techniques for training both CTR and CVR models. Two models share same user and item embeddings and similar neural network structures. The ranking model is also priceCTRCVR.

• CXR-RL : CXR-RL [24] is a recent value-aware recommendation algorithm that optimizes CTR and CVR simultaneously. CXR is designed as a combination of CTR and CVR. CXR-RL uses reinforcement learning techniques to optimize CXR, thus achieving a trade-off between CTR and CVR.

• PO-EA: PO-EA [28] is a state-of-the-art multi-objective recommendation approach which aims to find Pareto efficient solutions. PO-EA assumes that different elementary algorithms have different advantages on the objectives. It aggregates the scores given by multiple elementary algorithms and the weights are generated with an evolutionary algorithm. The elementary algorithms include LETORIF-CTR, LETORIF, CXR-RL, PE-LTR-CTR, and PE-LTR-GMV. LETORIF-CTR refers to the CTR model in LETORIF. Both PE-LTR-CTR and PE-LTR-GMV are PE-LTR models whose boundary constraints are added to optimize CTR and GMV correspondingly. The two LTR models are used as elementary algorithms for a fair comparison with PE-LTR.

• PO-EA-CTR, PO-EA-GMV: two solutions generated by PO-EA, which focus on CTR and GMV respectively.

• PE-LTR-CTR, PE-LTR-GMV: two solutions generated by PE-LTR, which focus on CTR and GMV respectively.

• ItemCF：基于item的协同过滤[31]。

• LambdaMART[37]是一种最先进的排序学习方法。利用MART模型对NDCG的可微损失进行了优化。然而，LambdaMART只关注点击相关性，而不考虑购买。

• LETORIF[36]是一种最近的GMV最大化排序学习方法，采用priceCTRCVR进行排序，其中CTR和CVR是来自两个独立模型的预测。

• MTL-REC:MTL-REC[21]采用多任务学习技术训练CTR和CVR模型。两个模型共享相同的user和item embedding以及相似的神经网络结构。排序模型也是priceCTRCVR。

• CXR-RL:CXR-RL[24]是一种最新的值感知推荐算法，它同时优化CTR和CVR。CXR设计为CTR和CVR的组合。CXR-RL使用强化学习技术来优化CXR，从而实现CTR和CVR之间的权衡。

• PO-EA:PO-EA[28]是一种最新的多目标推荐方法，旨在找到Pareto有效的解决方案。PO-EA假设不同的基本算法在目标上有不同的优势。它对多个基本算法给出的分数进行聚类，并用进化算法生成权重。基本算法包括LETORIF-CTR，LETORIF，CXR-RL、PE-LTR-CTR和PE-LTR-GMV。LETORIF-CTR是指LETORIF中的CTR模型。PE-LTR-CTR和PE-LTR-GMV都是PE-LTR模型，在模型中加入边界约束，对CTR和GMV进行相应的优化。两个LTR模型被用作基本算法，以便与PE-LTR进行公平比较。

• PO-EA-CTR、PO-EA-GMV：由PO-EA生成的两个解决方案，分别侧重于CTR和GMV。

• PE-LTR-CTR、PE-LTR-GMV：由PE-LTR生成的两种解决方案，分别针对CTR和GMV。

6.2.2 Experimental Settings. 实验设置

We adopt two typical IR metrics for CTR evaluation, i.e. NDCG and MAP. Meanwhile, we propose two GMV variants for both metrics:
我们采用了两种典型的IR指标来评估CTR，即NDCG和MAP。同时，我们为这两个指标提出了两种GMV变体：

where $Q_R$ denotes the set of purchased items, $pa{y}_i$ = 1/0 denotes
the whether the item at i-th rank is purchased or not, $pric{e}_i\prime$ denotes the price of the item at i-th rank, G-IDCG@K denotes the maximum possible value of G-DCG@K. G-NDCG considers the position biased GMV in the list, and prefers higher-ranking items that are purchased, while G-MAP considers the number of purchases in the recommendation list. For users without purchase records, the values of two metrics are both 0.
其中，$Q_R$表示购买的item，$pa{y}_i$ = 1/0表示排序为i的物品是否购买，$pric{e}_i\prime$表示第i个物品的价格，G-IDCG@K表示G-DCG@K的最大可能值，G-NDCG考虑列表中的位置偏差GMV，优先购买排名较高的物品，G-MAP考虑推荐列表中的购买数量。对于没有购买记录的用户，两个度量值都为0。

6.3 Offline Experimental Results 离线实验结果

6.3.1 Comparison with baselines 与基线的比较

To answer the first research question, we present the comparison on NDCG, MAP and the GMV-related metrics in Table 2. PE-LTR is the model selected from Pareto Front with fairness marginal utility and PO-EA is a PO-EA model with comparable CTR metrics with PE-LTR. As shown in the table, PE-LTR outperforms other approaches on all GMV related metrics and a comparable performance with LambdaMART on CTR related metrics. Compared with Item-CF and LambdaMART, PE-LTR achieves much higher G-NDCG and G-MAP. This is reasonable since PE-LTR jointly optimize the GMV and CTR while GMV is not optimized in Item-CF and LambdaMART. Meanwhile, PE-LTR achieves comparable NDCG and MAP with LambdaMART. In previous observations on benchmark studies of web search, LambdaMART is usually the best performing method [36, 37]. This indicates the effectiveness of our framework, which not only optimizes GMV but also guarantees a high CTR.
为了回答第一个研究问题，我们在表2中给出了NDCG、MAP和GMV相关指标的比较。PE-LTR是从具有公平边际效用的帕累托前沿选择的模型，PO-EA是具有可比CTR指标和PE-LTR指标的PO-EA模型。如表所示，PE-LTR在所有GMV相关指标上都优于其他方法，在CTR相关指标上也优于LambdaMART。与CF和LambdaMART相比，PE-LTR可以获得更高的G-NDCG和G-MAP。这是合理的，因为PE-LTR联合优化了GMV和CTR，而GMV在Item-CF和LambdaMART中没有优化。同时，PE-LTR实现了与LambdaMART相当的NDCG和MAP。在以往对网络搜索基准研究的观察中，Lamb-daMART通常是表现最好的方法[36，37]。这表明了我们的框架的有效性，它不仅优化了GMV，而且保证了较高的CTR。

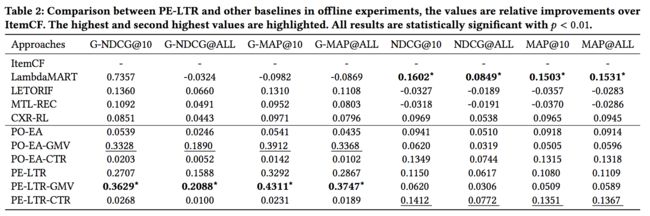
Compared with LETORIF, MTL-REC, CXR-RL and PO-EA, PE- LTR achieves higher G-NDCG and G-MAP, and at a much lower cost of CTR. There are several reasons behind this:
与LETORIF、MTL-REC、CXR-RL和PO-EA相比，PE-LTR可以实现更高的G-NDCG和G-MAP，并且成本更低。这背后有几个原因：

First, compared with LETORIF and MTL-REC, PE-LTR jointly learns both objectives with a single model, which allows the model to learn clicks and purchases simultaneously; While in LETORIF and MTL-REC, two separate models or components are designed for clicks and purchases, which may cause some inconsistency.
首先，与LETORIF和MTL-REC相比，PE-LTR使用单一模型共同学习这两个目标，使模型能够同时学习点击和购买；而在LETORIF和MTL-REC中，为点击和购买设计了两个独立的模型或组件，这可能会导致一些不一致。

Second, compared with CXR-RL and PO-EA, PE-LTR coordinates two objectives in a Pareto efficient way. CXR-RL optimizes both objectives, yet in a non-Pareto efficient way. Meanwhile, although PO-EA attempts to find Pareto efficient solutions, it only guarantees that the final solution is selected from a series of solutions that are not dominated by each other. We further plot the NDCG versus G-NDCG curve of PO-EA and PE-LTR in Fig 2 (Due to page limit, we just plot G-NDCG and NDCG in the figures of the paper, and the results are similar for MAP and G-MAP). As the figure shows, any solution generated by PO-EA is not dominated by the other one from PO-EA; and the case is same with PE-LTR. However, we observe that the curves of PE-LTR are above the curves of PO-EA, which means the solutions from PO-EA are dominated by those generated by PE-LTR. Note that two PE-LTR algorithms are already used as the elementary components in PO-EA, the comparison indicates that the proposed framework is more capable to generate Pareto efficient solutions.
其次，与CXR-RL和PO-EA相比，PE-LTR有效地协调了两个目标。CXR-RL也同时优化了这两个目标，但是是以非帕累托有效的方式。同时，虽然PO-EA试图找到帕累托有效解，但它只能保证最终解是从一系列互不支配的解中选择出来的。在图2中，我们进一步绘制了PO-EA和PE-LTR的NDCG与G-NDCG曲线（由于页数限制，我们仅在本文的图中绘制了G-NDCG和NDCG，结果与MAP和G-MAP相似）。如图所示，由PO-EA生成的任何解都不受来自PO-EA的另一个解的支配，与PE-LTR的情况相同，但我们观察到PE-LTR的曲线高于PO-EA的曲线，这意味着PO-EA的解被PE-LTR生成的解所支配。注意到两个PE-LTR算法已经被用作PO-EA的基本组件，比较表明，所提出的框架更能生成Pareto有效解。

Moreover, the real-world data in E-Commerce platforms may not follow the typical i.i.d. assumption. And scalarization weights are adjusted every batch in PE-LTR, which allows it to adjust to the training data dynamically during the training process. Meanwhile, PO-EA requires several well-trained algorithms for aggregation, which makes it more difficult to meet the requirements of online learning environments.
此外，电子商务平台中的真实数据可能不遵循典型的i.i.d.假设。在PE-LTR中，每一批训练数据都会调整标度化权重，使其在训练过程中能够动态地适应训练数据。同时，PO-EA需要多个经过良好训练的聚合算法，这使得在线学习环境的要求更加难以满足。

We further compare the quality of recommendations at the top of the ranking list. Since users usually focus more on the top-ranked items, the metrics at the top are more important in recommendation. The results are presented in Fig 3 . As shown in the figures, PE- LTR outperforms the other baselines on GMV related metrics, and at a low cost of CTR. This illustrates the importance of Pareto efficiency in real-world recommender systems. Optimizing a single objective alone may hurt the other objectives severely. Therefore it is necessary to jointly consider multiple objectives simultaneously and a Pareto efficiency recommendation makes it possible to achieve high GMV at a low cost of CTR.
我们进一步比较了排名第一的推荐的质量。由于用户通常更关注排名靠前的物品，因此排名靠前的指标在推荐中更为重要。结果如图3所示。如图所示，PE-LTR在GMV相关指标上优于其他基线，且对CTR伤害较小。这说明了帕累托效率在现实推荐系统中的重要性。单独优化一个目标可能会严重损害其他目标。因此，有必要同时考虑多个目标，帕累托效率建议使得以较低的CTR成本实现高GMV成为可能。

6.3.2 The Pareto Efficiency of PE-LTR. PE-LTR的帕累托效率

To answer the second research question, we first generate the Pareto Frontier of CTR and GMV losses by running Alg. 1 with different bounds and plot the Pareto Frontier in Fig 2. It can be observed that the losses under different constraints basically follow Pareto efficiency, i.e. no point achieves both lower CTR and GMV losses than other points. When the model focuses more on CTR, CTR loss is lower and GMV loss is higher, and vice versa. This coincides with the Pareto efficient scalarization scheme of the proposed framework.
为了回答第二个研究问题，我们首先通过运行Alg.1生成CTR和GMV损失的帕累托边界。用不同的边界，在图2中画出帕累托边界。可以看出，不同约束条件下的损耗基本上遵循帕累托效率，即没有一个点能同时达到比其他点更低的CTR和GMV损耗。当模型更关注中心时，中心损失较低，GMV损失较高，反之亦然。这与该框架的Pareto有效尺度化方案相吻合。

Then we compare the solution of PE-LTR under different solution selection strategies. We predefine two series of bounds for ctr and gmv: ($w_{ctr}\ge 0,omeg{a}_{gmv}\ge 0.8$) and ($w_{ctr}\ge 0.8,omeg{a}_{gmv}\ge 0.0$), and get two PE-LTRs (PE-LTR-GMV and PE-LTR-CTR) which focus on GMV and CTR respectively. Then we choose two PE-LTRs (PE-LTR-LM and PE-LTR-MU) from the Pareto Frontier with LM fairness and MU fairness. We plot the comparison between these PE-LTRs in Fig 4.
然后比较了不同的方案选择策略下PE-LTR的方案。我们预先定义了ctr和gmv的两个界：($w_{ctr}\ge 0,omeg{a}_{gmv}\ge 0.8$) 和 ($w_{ctr}\ge 0.8,omeg{a}_{gmv}\ge 0.0$)，得到了两个分别聚焦于gmv和ctr的PE-LTR（PE-LTR-gmv和PE-LTR-ctr）。然后从帕累托边界选择两个具有LM公平和MU公平的PE-LTR-LM和PE-LTR-MU。我们在图4中绘制了这些PE-LTR之间的比较。

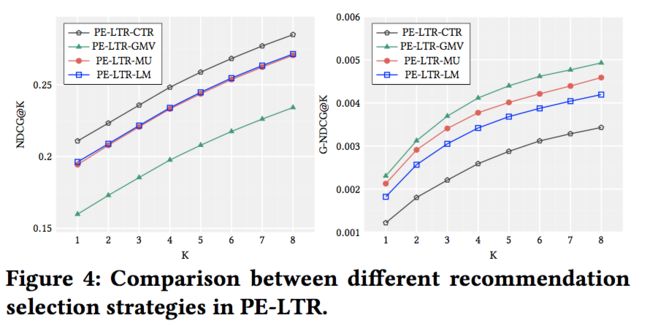
The performances of PE-LTR-CTR and PE-LTR-GMV are consistent with the constraints added to the objectives. Therefore when the priority of GMV and CTR are available (i.e. GMV or CTR is preferred), the recommendation can be achieved by setting the bounds correspondingly. When the priorities are not available, a fair solution can be achieved by selecting from Pareto Frontier with highest fairness. Despite the performance of selected PE-LTR (PE- LTR-LM and PE-LTR-MU) is not the best on all metrics, it achieves a relatively good trade-off between the two objectives. Comparing PE-LTR-LM with PE-LTR-MU, we find the two recommendations selected with LM and MU fairness are relatively balanced. PE-LTR-MU outperforms PE-LTR-LM in GMV while PE-LTR-LM is slightly better in CTR.
PE-LTR-CTR和PE-LTR-GMV的性能与目标附加的约束条件一致。因此，当GMV和CTR的优先级可用时（即优选GMV或CTR），可以通过相应地设置界限来实现推荐。当优先级不可用时，可以通过从具有最高公平性的Pareto边界中进行选择来实现公平解决。尽管所选择的PE-LTR（PE-LTR-LM和PE-LTR-MU）在所有指标上都不是最好的，但它在两个目标之间实现了相对良好的权衡。比较PE-LTR-LM和PE-LTR-MU，我们发现用LM和MU公平性选择的两种推荐是相对平衡的。在GMV上，PE-LTR-MU优于PE-LTR-LM，而在CTR上，PE-LTR-LM稍好。

6.3.3 The Scalability of PE-LTR. PE-LTR的可扩展性

To answer the third research question, we conduct experiments to show the scalability of PE-LTR in terms of model selection. We use LR, DNN and WDL as the model in PE-LTR framework, and the details of the models can be found in Section 5. We set same bounds for the models and the results are plotted in Fig 5.
为了回答第三个研究问题，我们进行了实验，从模型选择的角度展示了PE-LTR的可扩展性。我们使用LR、DNN和WDL作为PE-LTR框架中的模型，模型的详细内容见第5节。我们为模型设置了相同的边界，结果如图5所示。

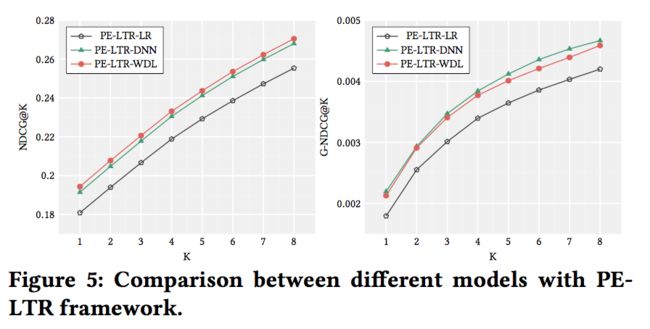
Judging from the results, we observe that the model selection has an important impact on the performance of PE-LTR. Among the three PE-LTR variants, PE-LTR-WDL outperforms the rest and PE- LTR-DNN outperforms PE-LTR-LR. This is reasonable since neural networks capture more complex relationships between features than linear models. And Wide&Deep model combines both neural networks and linear models into a single model, which enables better generalization and memorization for recommendation [9]. Therefore, PE-LTR is able to accommodate with varies kinds of models and stronger models can lead to better performances. This also illustrates the potential of PE-LTR, whose performance can be further enhanced by more carefully designed models.
从结果可以看出，模型的选择对PE-LTR的性能有重要影响，在三种PE-LTR变体中，PE-LTR-WDL的性能优于其余的，PE-LTR-DNN的性能优于PE-LTR-LR。这是合理的，因为神经网络比线性模型捕捉到更复杂的特征之间的关系。而广度和深度模型将神经网络和线性模型结合成一个单一的模型，这样可以更好地泛化和记忆推荐信息[9]。因此，PE-LTR能够适应不同的模型，更强的模型可以带来更好的性能。这也说明了PE-LTR的潜力，其性能可以通过更精心设计的模型进一步提高。

6.4 Online Experimental Results 在线实验结果

The online experiments are conducted on the real-world E-Commerce platform for three days. For online experiments, CTR-only approaches hurt GMV severely. Therefore, the approaches that only concern with CTR are not included in the online experiments.
在线实验在现实世界的电子商务平台上进行了三天。对于在线实验，只优化CTR的方法会严重伤害GMV。因此，在线实验中不包括只涉及CTR的方法。

We concern with four metrics in the online experiments, i.e.CTR (Click Through Rate), IPV (Individual Page View), PAY (number of payments) and GMV (Gross Merchandise Volume). We compute the average performances of three days and present the results in Table 3. Due to the large number of users, the results are statistically significant. We use LETORIF as the baseline, and present the relative improvements of compared approaches on LETORIF in the table.
在线实验中，我们关注四个指标，即点击率（CTR）、个人页面浏览量（IPV）、支付量（PAY）和商品总量（GMV）。我们计算了三天的平均性能，结果见表3。由于用户众多，结果具有统计学意义。我们以LETORIF为基线，在表中给出了所比较的方法对LETORIF的相对改进。

From the results we observe that our approaches outperform other baselines on all the four metrics. This basically coincides with the offline experimental results. Note that PE-LTR achieves significant improvements on GMV with a high CTR, this illustrates the advantage of Pareto efficient recommendation. Meanwhile, PO-EA requires offline models for aggregation and can not learn the weights online, making it less effective in the experiments.
从结果来看，我们的方法在所有四个指标上都优于其他基线。这与离线实验结果基本吻合。请注意，PE-LTR以较高的CTR在GMV上实现了显著的改进，这说明了帕累托有效推荐的优势。同时，PO-EA需要离线模型进行聚合，不能在线学习权值，实验效率也比较差。