算法学习总结

推荐两个算法文章：

基本算法：https://www.cnblogs.com/chengxiao/p/6194356.html

动态图的算法：https://www.cnblogs.com/onepixel/articles/7674659.html

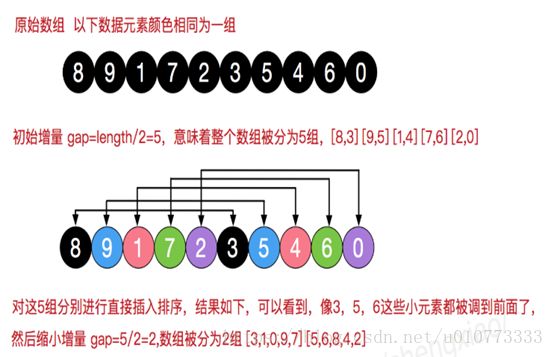
希尔排序

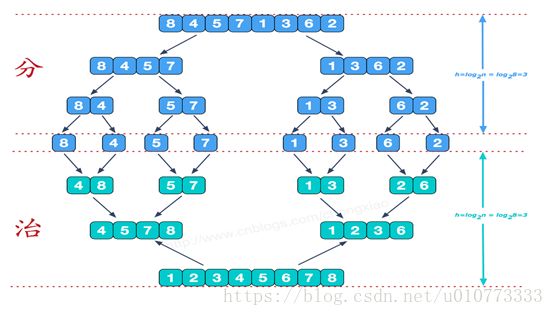
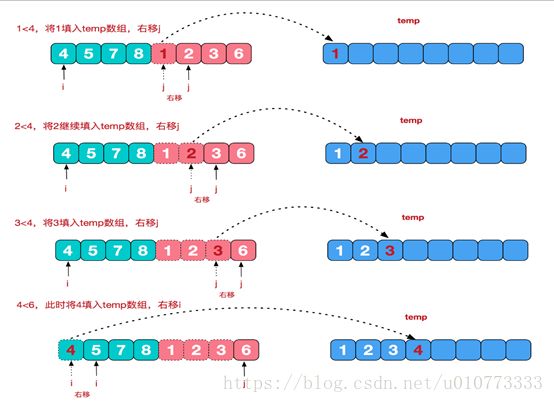
归并算法

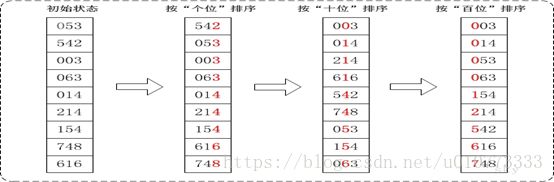
基数排序

桶排序

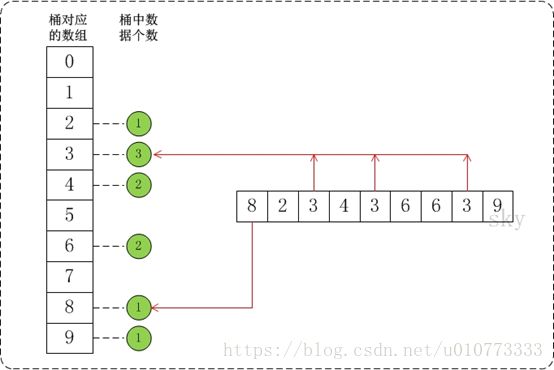
桶排序(Bucket Sort)的原理很简单，它是将数组分到有限数量的桶子里。

假设待排序的数组a中共有N个整数，并且已知数组a中数据的范围[0, MAX)。在桶排序时，创建容量为MAX的桶数组r，并将桶数组元素都初始化为0；将容量为MAX的桶数组中的每一个单元都看作一个"桶"。
在排序时，逐个遍历数组a，将数组a的值，作为"桶数组r"的下标。当a中数据被读取时，就将桶的值加1。例如，读取到数组a[3]=5，则将r[5]的值+1。

https://blog.csdn.net/crazygolf/article/details/40378255

计数排序

假设数序列中小于元素a的个数为n，则直接把a放到第n+1个位置上。当存在几个相同的元素时要做适当的调整，因为不能把所有的元素放到同一个位置上。计数排序假设输入的元素都是0到k之间的整数。

 

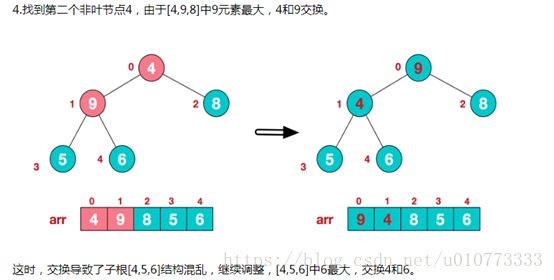
堆排序(二叉树)

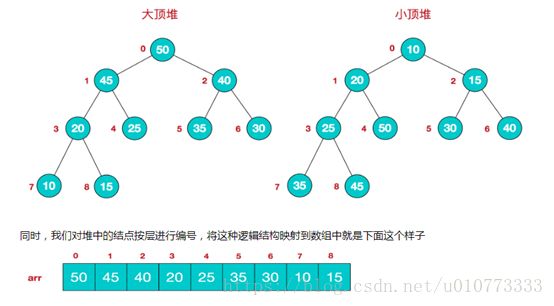
堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。

 

堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。首先简单了解下堆结构。

该数组从逻辑上讲就是一个堆结构，我们用简单的公式来描述一下堆的定义就是：

大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]  

小顶堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]  

 

 

 

 

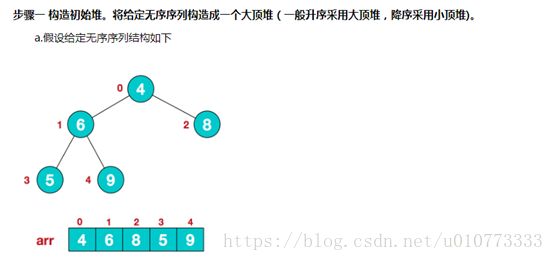
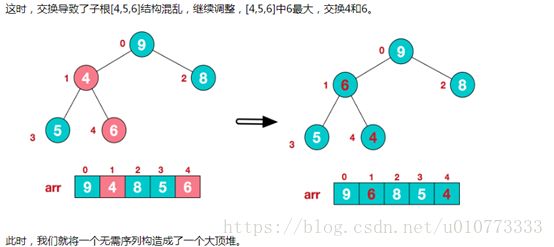
再简单总结下堆排序的基本思路：

　　a.将无需序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆;

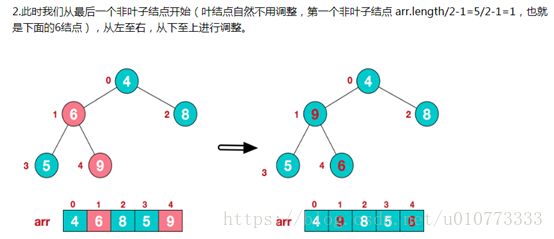
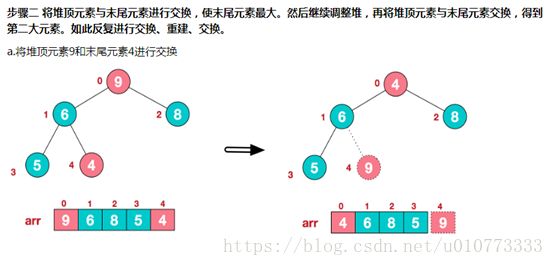
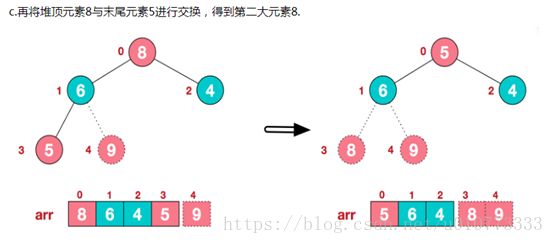
　　b.将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;

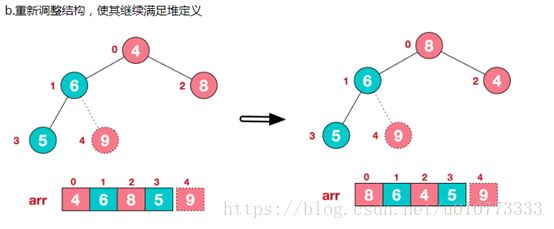
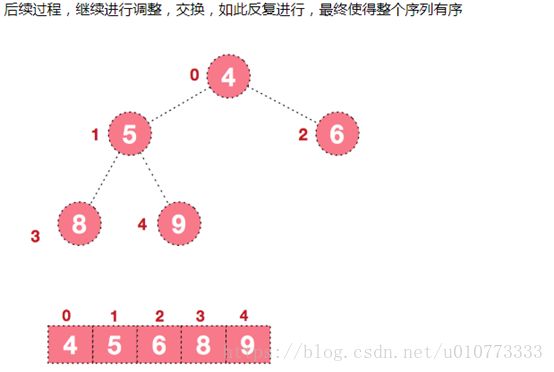
　　c.重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。

 二叉树排序

      二叉树排序法借助了数据结构二叉排序树，二叉排序数满足三个条件：（1）若左子树不空，则左子树上所有结点的值均小于它的根结点的值； （2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值； （3）左、右子树也分别为二叉排序树。根据这三个特点，用中序遍历二叉树得到的结果就是排序的结果。

      二叉树排序法需要首先根据数据构建二叉排序树，然后中序遍历，排序时间复杂度为O(nlogn)，构建二叉树需要额外的O(n)的存储空间，有相同的元素是可以设置排在后边的放在右子树，在中序变量的时候也会在后边，所以二叉树排序是稳定的。

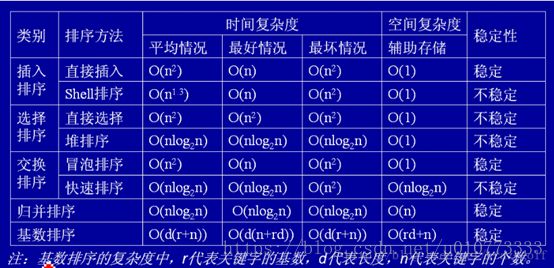
排序的分类/稳定性/时间复杂度和空间复杂度总结

排序的稳定性和复杂度

      不稳定：

      选择排序（selection sort）— O(n2)

      快速排序（quicksort）— O(nlogn) 平均时间, O(n2) 最坏情况; 对于大的、乱序串列一般认为是最快的已知排序

      堆排序 （heapsort）— O(nlogn)

      希尔排序 （shell sort）— O(nlogn)

      基数排序（radix sort）— O(n·k); 需要 O(n) 额外存储空间 （K为特征个数）

 

      稳定：

      插入排序（insertion sort）— O(n2)

      冒泡排序（bubble sort） — O(n2)

      归并排序 （merge sort）— O(n log n); 需要 O(n) 额外存储空间

      二叉树排序（Binary tree sort） — O(nlogn); 需要 O(n) 额外存储空间

      计数排序  (counting sort) — O(n+k); 需要 O(n+k) 额外存储空间，k为序列中Max-Min+1

      桶排序 （bucket sort）— O(n); 需要 O(k) 额外存储空间

 

对称加密AES，非对称加密: ECC，消息摘要: MD5，数字签名:DSA

简单的加密设计： 用密钥对原文做  异或，置换，代换，移位

 

MD5将任意长度的“字节串”变换成一个128bit的大整数，并且它是一个不可逆的字符串变换算法

MD5还广泛用于加密和解密技术上，在很多操作系统中，用户的密码是以MD5值（或类似的其它算法）的方式保存的， 用户Login的时候，系统是把用户输入的密码计算成MD5值，然后再去和系统中保存的MD5值进行比较，而系统并不“知道”用户的密码是什么。

MD5主要用途：

1、对一段信息生成信息摘要，该摘要对该信息具有唯一性,可以作为数字签名。

2、用于验证文件的有效性(是否有丢失或损坏的数据),

3、对用户密码的加密，

4、在哈希函数中计算散列值

 

非对称加密: ECC(160位)或RSA(1024)

RSA加密算法

在谈RSA加密算法之前，我们需要先了解下两个专业名词，对称加密和非对称加密。

对称加密即：含有一个称为密钥的东西，在消息发送前使用密钥对消息进行加密，在对方收到消息之后，使用相同的密钥进行解密

非对称加密即：加密和解密使用不同的密钥的一类加密算法。这类加密算法通常有两个密钥A和B，使用密钥A加密数据得到的密文，只有密钥B可以进行解密操作（即使密钥A也无法解密），相反，使用了密钥B加密数据得到的密文，只有密钥A可以解密。这两个密钥分别称为私钥和公钥，顾名思义，私钥就是你个人保留，不能公开的密钥，而公钥则是公开给加解密操作的另一方的。根据不同用途，对数据进行加密所使用的密钥也不相同（有时用公钥加密，私钥解密；有时相反用私钥加密，公钥解密）。非对称加密的代表算法是RSA算法。

缺点 它产生密钥很麻烦，受到素数产生技术的限制，因而难以做到一次一密，分组长度太大等

 

DES加密

DES加密：使用一个 56 位的密钥以及附加的 8 位奇偶校验位，产生最大 64 位的分组大小。这是一个迭代的分组密码，使用称为 Feistel 的技术，其中将加密的文本块分成两半。使用子密钥对其中一半应用循环功能，然后将输出与另一半进行“异或”运算；接着交换这两半，这一过程会继续下去，但最后一个循环不交换。DES 使用 16 个循环，使用异或，置换，代换，移位操作四种基本运算。额专业术语就看看得了，下面直接给大家演示一个小demo，以帮助大家的理解。