计算机视觉相机标定——python

一、棋盘格制作

1. 制作棋盘格

2. 并且将棋盘格固定放到一个平板上，使用同一相机从不同的位置，不同的角度，拍摄标定板的多张照片（10-20张左右），将照片放到文件夹中：

二、像机标定

利用摄像机所拍摄到的图像来还原空间中的物体。在这里，不妨假设摄像机所拍摄到的图像与三维空间中的物体之间存在以下一种简单的线性关系：[像]=M[物],这里，矩阵M可以看成是摄像机成像的几何模型。 M中的参数就是摄像机参数。通常，这些参数是要通过实验与计算来得到的。这个求解参数的过程就称为摄像机标定。

张正友平面标定方法

张正友标定是指张正友教授1998年提出的单平面棋盘格的摄像机标定方法。本文中提出的方法介于传统标定法和自标定法之间，但克服了传统标定法需要的高精度标定物的缺点，而仅需使用一个打印出来的棋盘格就可以。同时也相对于自标定而言，提高了精度，便于操作。因此张氏标定法被广泛应用于计算机视觉方面。
世界坐标系（world coordinate）$(xw,yw,zw)$，也称为测量坐标系，是一个三维直角坐标系，以其为基准可以描述相机和待测物体的空间位置。世界坐标系的位置可以根据实际情况自由确定。
相机坐标系（camera coordinate）$(xc,yc,zc)$，也是一个三维直角坐标系，原点位于镜头光心处，x、y轴分别与相面的两边平行，z轴为镜头光轴，与像平面垂直。
像素坐标系 $uov$是一个二维直角坐标系，反映了相机中像素的排列情况。原点o位于图像的左上角，u轴、v轴分别于像面的两边平行。像素坐标系中坐标轴的单位是像素（整数）。
图像坐标系$XOY$，其坐标轴的单位通常为毫米（mm），原点是相机光轴与相面的交点（称为主点），即图像的中心点，X轴、Y轴分别与u轴、v轴平行。故两个坐标系实际是平移关系，即可以通过平移就可得到。
2. 计算单应性矩阵H
设三维世界坐标的点为$X=[X,Y,Z,1{]}^T$,二维相机平面像素坐标为$m=[u,v,1{]}^T$,所以标定用的棋盘格平面得到图像平面的单应性关系为：
$s0m=K[R,T]X$
其中，s为尺度因子，k为摄像机内参数，R为旋转矩阵，T为平移向量。令
$K=\left[\begin{array}{ccc}\alpha & \beta & u_0\\ 0& \gamma & v_0\\ 0& 0& 1\end{array}\right]$
s做为齐次坐标来说，不会改变齐次坐标值。将世界坐标系构造在棋盘格平面上，令棋盘格平面为Z=0的平面。则
$s\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=K\left[\begin{array}{cccc}r1& r2& r3& 1\end{array}\right]\left[\begin{array}{c}X\\ Y\\ 0\\ 1\end{array}\right]=K\left[\begin{array}{ccc}r1& r2& t\end{array}\right]\left[\begin{array}{c}X\\ Y\\ 1\end{array}\right]$
将$K[r1,r2,t]$叫做单应性矩阵H，即：
$s\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=H\left[\begin{array}{c}X\\ Y\\ 1\end{array}\right]$
H是一个齐次矩阵，所以有八个未知数，至少需要八个方程，每对对应点能提供两个方程，所以至少需要四个对应点，就可以算出世界平面到图像平面的单应性矩阵H。

3. 计算内参数矩阵
   由上述可知，
   $\lambda =\frac{1}{S}$

$r1=\frac{1}{\lambda }{K}^{-1}h1$

$r2=\frac{1}{\lambda }{K}^{-1}h2$
由于旋转矩阵中，r1和r2都正交，可得
$r_1^{T}r2=0$

$\Vert \begin{array}{c}r1\end{array}\Vert =\Vert \begin{array}{c}r2\end{array}\Vert =1$
代入可得：
$h_1^T{K}^{-T}{K}^{-T}{h}_2=0$
$h_1^T{K}^{-T}{K}^{-T}{h}_1=h_2^T{K}^{-T}{K}^{-T}{h}_2$
即每个单应性矩阵能提供两个方程，而内参数矩阵包含五个参数，要求解的话至少需要三个单应性矩阵。为了得到三个不同的单应性矩阵，我们使用至少三幅棋盘格平面的图片进行标定。通过改变相机与标定板之间的相对位置来得到达三个不同的图片。定义如下：

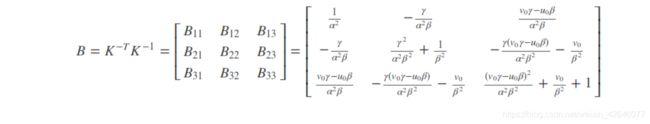
可以看出。B是一个对称阵，所以B的有效元素为六个，让这六个元素写成向量b，即

可以推导得到

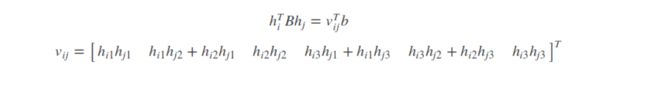
利用约束条件可以得到：

通过上式，我们至少需要三幅包含棋盘格的图像，可以计算得到B，然后通过cholesky分解，得到相机的内参数矩阵K。

4. 计算外参数矩阵
   由之前的推导可得：
   

5. 最大似然估计
   由于可能存在高斯噪声，所以使用最大似然估计进行优化。这里使用的是多参数非线性系统优化问题的Levenberg-Marquardt算法进行迭代优化求最优解。
   

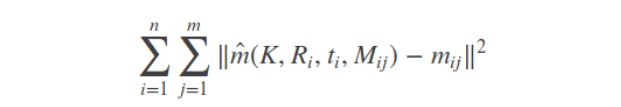
6. 径向畸变估计
   数学表达式：
   
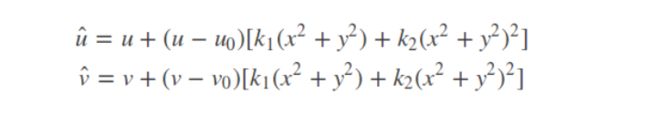
   其中，$(u,v)$是理想无畸变的像素坐标，$(\hat{u},\hat{v})$是实际畸变后的像素坐标。$(u0,v0)$代表主点，$(x,y)$是理想无畸变的连续图像坐标，$(\hat{x},\hat{y})$是实际畸变后的连续图像坐标。k1和k2为前两阶的畸变参数。
   $\hat{u}=u_0+\alpha \hat{x}+\gamma \hat{y}$
   $\hat{v}=v_0+\beta \hat{y}$
   化作矩阵形式：
   $\left[\begin{array}{cc}(u-u_0)(x^2+y^2)& (u-u_0)(x^2+y^2{)}^2\\ (v-v_0)(x^2+y^2)& (v-v_0)(x^2+y^2{)}^2\end{array}\right]\left[\begin{array}{c}k1\\ k2\end{array}\right]=\left[\begin{array}{c}\hat{u}-u\\ \hat{v}-v\end{array}\right]$
   记做：$Dk=d$
   则可得：$k={\left[\begin{array}{cc}k1& k2\end{array}\right]}^T=(D^{T}D{)}^{-1}{D}^{T}d$
   计算得到畸变系数k。
   由此，我们得到了相机内参，外参和畸变系数。

三、算法描述

1. 打印一张模板并贴在一个平面上；

2. 从不同角度拍摄若干张模板图像；

3. 检测出图像中的特征点；

4. 求出摄像机的内参数和外参数；

5. 求出畸变系数；

6. 优化求精。

四、标记实验

1. 选择标定物
   

2. 提取角点
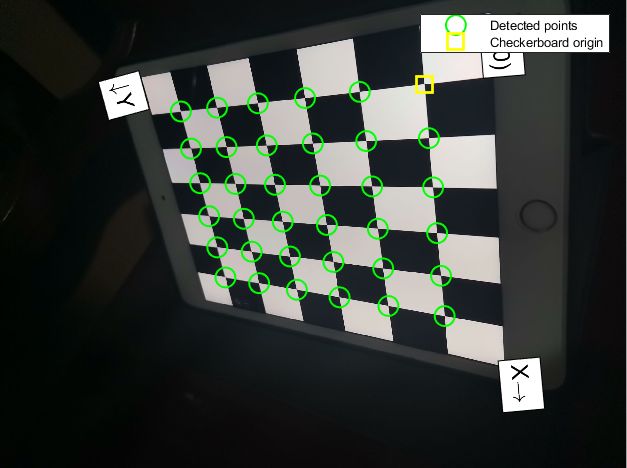
   OpenCV中自带了提取棋盘格中内角点的函数：findChessboardCorners()。这个函数的功能是确定输入图像中是否有棋盘格图案，并检测棋盘格的内角点。如果所有的内角点都找到了，那么函数返回一个非0值；如果没有找到所有的内角点，就会返回0。 因为我们使用的是有9×5的内格子，所以我们在设置w和h时分别填写9和5。函数返回每一一个角点，如果匹配到了模式，它将返回是True。这些角点将按一定顺序标注出来（从左到右，从上到下）。

3. 相机参数：
   内参数矩阵mtx,
   畸变系数dist,
   旋转向量rvecs,
   平移向量tvecs,

('ret:', 2.3186098655428147)
('mtx:\n', array([[1.85926419e+03, 0.00000000e+00, 9.83685393e+02],
       [0.00000000e+00, 4.68377568e+03, 7.37895380e+02],
       [0.00000000e+00, 0.00000000e+00, 1.00000000e+00]]))
('dist:\n', array([[-4.39285275e-02, -3.28071108e+00,  1.23540410e-02,
         6.44947962e-02,  1.42250729e+01]]))
('rvecs:\n', [array([[ 1.44167192],
       [-0.24655605],
       [ 0.20024858]]), array([[-0.94274122],
       [-0.68501983],
       [-0.64018825]])])
('tvecs:\n', [array([[-7.20990569],
       [-1.66197584],
       [16.45940596]]), array([[-9.35227557],
       [-3.42757968],
       [24.79553047]])])

4. 实验代码：

# -*- coding: utf-8 -*-
import cv2
import numpy as np
import glob

# 设置寻找亚像素角点的参数，采用的停止准则是最大循环次数30和最大误差容限0.001
criteria = (cv2.TERM_CRITERIA_MAX_ITER | cv2.TERM_CRITERIA_EPS, 30, 0.001)

# 获取标定板角点的位置
objp = np.zeros((6 * 6, 3), np.float32)
objp[:, :2] = np.mgrid[0:6, 0:6].T.reshape(-1, 2)  # 将世界坐标系建在标定板上，所有点的Z坐标全部为0，所以只需要赋值x和y

obj_points = []  # 存储3D点
img_points = []  # 存储2D点

images = glob.glob(r"D:\CVphoto\0407\*.jpg")
for fname in images:
    img = cv2.imread(fname)
    cv2.imshow('img',img)
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

    size = gray.shape[::-1]
    ret, corners = cv2.findChessboardCorners(gray, (6, 6), None)
    print(ret)

    if ret:

        obj_points.append(objp)

        corners2 = cv2.cornerSubPix(gray, corners, (5, 5), (-1, -1), criteria)  # 在原角点的基础上寻找亚像素角点
        #print(corners2)
        if [corners2]:
            img_points.append(corners2)
        else:
            img_points.append(corners)

        cv2.drawChessboardCorners(img, (6, 6), corners, ret)  # 记住，OpenCV的绘制函数一般无返回值
        cv2.imshow('img', img)
        cv2.waitKey(2000)

print(len(img_points))
cv2.destroyAllWindows()

# 标定
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(obj_points, img_points, size, None, None)

print("ret:", ret)
print("mtx:\n", mtx) # 内参数矩阵
print("dist:\n", dist)  # 畸变系数   distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
print("rvecs:\n", rvecs)  # 旋转向量  # 外参数
print("tvecs:\n", tvecs ) # 平移向量  # 外参数

print("-----------------------------------------------------")

5. 出现问题：

  File "D:/computervisionjob/zhangzhengyou.py", line 45, in <module>
    ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(obj_points, img_points, size, None, None)
error: C:\projects\opencv-python\opencv\modules\calib3d\src\calibration.cpp:3334: error: (-215) nimages > 0 in function cv::calibrateCamera

需要注意标定板的大小是标定板在水平和竖直方向上内角点的个数。内角点指的是，标定板上不挨着边界的角点（如图标定板大小为6×6）。
该问题出现了很多次，通过改变网格的长宽，改变网格的数量（6x9和6x7都有进行测试），改变拍摄角度等办法，这个问题都没有很好的消除，最后进行了一次6*6的的标定板实验，读出了两张图片。
所以初步判断是图片的问题，代码应该是可以使用的，具体要哪种类型的图片，我之后再探究一下。

五、matlab相机标定

1. matlab读入的图片大小要一致
   一共标记了八张图片

2. 参数可视化
   
   
   
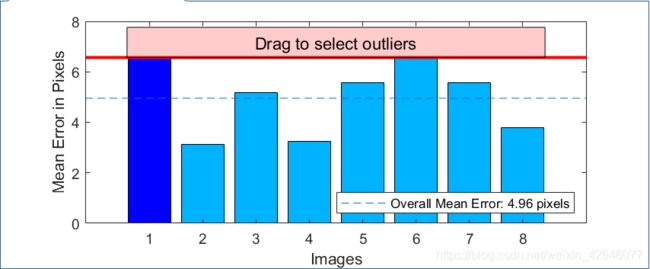
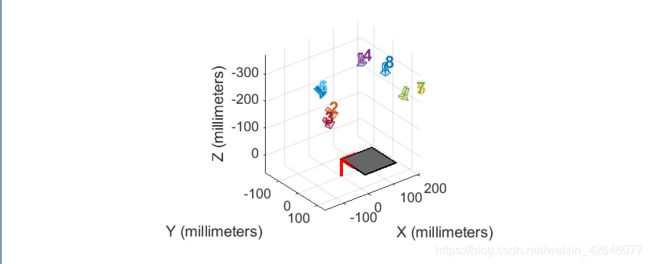
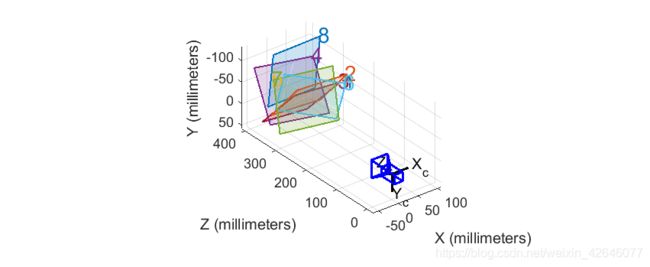
3. 小结：在进行matlab相机标定时提示图片的size要一样！！！
   因为是同一部手机进行拍摄的图片，所以之前并没有考虑是因为图片尺寸原因造成的pycharm中代码运行错误，但是那两张可以标记的图片size都是960x720的，但是不可以标记的都是1920x1440的，但是将文件夹图片的size都调整为1920x1440时，依然不能进行标记，所以之后会尝试调整图片size都是960x720的再尝试一次。

六、小结

OpenCV中自带了
1.提取棋盘格中内角点的函数：findChessboardCorners()，这个函数的功能是确定输入图像中是否有棋盘格图案，并检测棋盘格的内角点。如果所有的内角点都找到了，那么函数返回一个非0值；如果没有找到所有的内角点，就会返回0。
2.drawChessboardCorners函数，在图片中画出检测到的角点。
3.calibrateCamera是标定函数，也是相机标定的核心。
4.可以对图像进行畸变矫正，使用initUndistort函数来实现。
5.计算外参和内参做了很多推导，仅仅是为后面的极大似然参数估计提供初值。但当然这个初值也是不可或缺的，因为没有这个初值，就无法估计出更为准确的参数。
6.实验过程中那个错误一直没有得到解决，希望在后面的学习中可以找到方法。