聚类分析

一、监督学习和无监督学习

  监督学习是指从标注数据(训练集)中学习预测模型的机器学习问题。标注数据表示输入输出的对应关系，预测模型对给定的输入产生相应的输出。监督学习的本质是学习输入到输出的映射的统计规律。

  无监督学习是指从无标注数据中学习预测模型的机器学习问题。无标注数据是自然得到的数据，预测模型表示数据的类别、转换或者概率。无监督学习的本质是学习数据中的统计哦规律或潜在结构。

二、聚类分析

  聚类是数据挖掘和计算的基本任务，是将大量数据集中具有"相似"特征的数据点或样本划分为一个类别。聚类分析的基本思想是"物以类聚，人以群分"，因此大量的数据集中必然存在相似的数据样本，基于这个假设就可以将数据区分出来，并发现不同类的特征。

  聚类常用于数据探索或挖掘前期，在没有做先验经验的背景下做的探索性分析，也适用于样本量较大情况下的数据预处理工作。例如，针对企业整体的用户特征，在未得到相关知识或经验之前，先根据数据本身特点进行用户分群，然后针对不同群体作进一步分析；对连续数据离散化，便于后续做分类分析应用。

  常用的聚类算法分为基于划分、层次、密度、网格、统计学、模型等类型的算法，典型算法包括K均值，DBSCAN、两步聚类、BIRCH、谱聚类等。

  聚类分析能解决的问题包括：数据集可以分为几类、每个类别有多少样本量、不同类别中各个变量的强弱关系如何、不同类别的典型特征如何。除了划分类别等，聚类还能用于基于划分的其他应用，例如图片压缩等。

2.1 K-Means

  k均值是聚类中最常用的方法之一，它基于点与点距离的相似度来计算最佳类别归属。但K均值在应用之前一定要注意两种数据异常：

• 数据的异常值。数据中的异常值能明显改变不同点之间的距离相似度，并且这种影响是非常显著的。因此基于距离相似度的判别模式下，异常值的处理必不可少。
• 数据的异常量纲。不同的维度和变量之间，如果存在数值规模或量纲的差异，那么在做距离之前需要先将变量归一化或标准化。例如，跳出率的数值分布区间是[0,1]，订单金额可能是[0,1000000]，而订单数量则是[0,1000]。如果没有归一化或标准化操作，那么相似度将主要受到订单金额的影响。

2.2 DBSCAN

  当然，K均值并不是唯一的聚类方法，如果上述两种条件受某些因素的限制无法实现，那么可以选择其他聚类方法。例如DBSCAN，其中文含义是"基于密度的带有噪声的空间聚类"。DBSCAN是一个比较有代表性的基于密度的聚类算法，与基于划分和层次的聚类方法不同，他将簇定义为密度相连的点的最大集合，能够把具有足够高密度的区域划分为簇，并可在噪声的空间数据集中发现任意形状的聚类。

  DBSCAN算法的出发点是基于密度寻找被低密度区域分离的高密度空间，以此来实现不用数据样本的聚类。跟K均值相比，它具有以下优点：

• 原始数据集的分布规律没有明显要求，能适应任意数据集分布形状的空间聚类，因此数据集实用性更广，尤其是对非凸装、圆环形等异性簇分布的识别较好
• 无须指定聚类数量，对结果的先验要求不高
• 由于DBSCAN可区分核心对象、边界点和噪音点，因此对噪声的过滤效果好，能有效应对数据噪点。

  但是，由于他直接对整个数据集进行操作，且聚类时使用了一个全局性的表征密度的参数，因此也存在几个明显的弱点：

• 对于高维问题，基于Eps(半径)和MinPts(密度)的定义是个很大问题
• 当簇的密度变化太大时，聚类效果较差
• 当结果量增大时，要求较大的内存支持，I/O消耗也很好。

2.3 超大数据量时应该放弃K均值算法

  K均值在算法稳定性、效率和准确率上表现非常好，并且在应对大量数据时依然如此。他的算法时间复杂度上界为O(n* k * t)，其中n是样本量、k是划分的聚类数，t是迭代次数。当聚类数和迭代次数不变时，K均值的算法消耗时间只跟样本量有关，因此会呈线性增长趋势。

  当真正面对海量数据时，使用K均值算法将面临严重的结果延迟，尤其是当K均值被用作实时性或准实时性的数据预处理、分析和建模时，这种瓶颈效应尤为明显。针对K均值的这一问题，很多延伸算法出现了，MiniBatchKMeans就是其中一个典型代表。MiniBatch的好处是计算过程中不必使用所有的数据样本。由于计算样本量少，所以会相应减少运行时间；但另一方面，由于是抽样方法，抽样样本很难完全代表整体样本的全部特征，因此会带来准确度的下降。

2.4 高维数据上无法应用聚类吗？

  在大数据背景上，数据获取难度和成本非常低，很多高维数据场景例如电子商务交易数据、Web文本数据日益丰富。在做高维数据聚类时，传统的在低维空间通用的聚类方法运用到高维空间时，通常不能取得令人满意的聚类结果，主要表现在聚类计算耗时太长、聚类结果相对于真是标签分类的准确性和稳定性都大为降低

  应对高维数据的聚类主要有2种方法：降维、子空间聚类

  降维是应对高维数据的有效方法，通过特征选择法或维度转换法将高维空间降低或映射到低维空间，直接解决了高维问题

  子空间聚类算法是在高维数据空间中对传统聚类算法的一种扩展，其思想是选取与给定簇密切相关的维，然后在对应的子空间进行聚类。比如，谱聚类就是一种子空间聚类方法。

2.5 如何选择聚类分析算法？

聚类算法有几十种之多，聚类算法的选择主要参考以下因素：

• 如果数据集是高维的，那么选择谱聚类，他是子空间划分的一种
• 如果数据量为中小规模，例如在100万条以内，那么K均值将是比较好的选择；如果数据量超过100万条，那么可以考虑使用MiniBatchKMeans
• 如果数据集中有噪点，那么使用基于密度的DBSCAN可以有效应对这个问题。

三、K-Means算法

3.1 什么是K-Means算法？

作为聚类算法的典型代表，Kmeans可以说是最简单的聚类算法没有之一，那么他是怎么完成聚类的呢？

  KMeans算法将一组N个样本的特征矩阵X划分为K个无交集的簇，直观上来看是簇是一组一组聚集在一起的数据，在一个簇中的数据就认为是同一类。簇就是聚类的结果表现。
  簇中所有数据的均值 通常被称为这个簇的“质心”（centroids）。在一个二维平面中，一簇数据点的质心的横坐标就是这一簇数据点的横坐标的均值，质心的纵坐标就是这一簇数据点的纵坐标的均值。同理可推广至高维空间。

  在KMeans算法中，簇的个数K是一个超参数，需要我们人为输入来确定。KMeans的核心任务就是根据我们设定好的K，找出K个最优的质心，并将离这些质心最近的数据分别分配到这些质心代表的簇中去。

1. 随机抽取K个样本作为最初的质心
2. 开始循环
3. 将每个样本分配到离他们最近的质心，生成K个簇
4. 对于每个簇，计算所有被分到该簇的样本点的平均值作为新的质心
5. 当质心的位置不再发生变化，迭代停止，聚类完成

3.2 什么是簇内误差平方和？

  我们认为聚类算法聚出的类，也就是被分在同一个簇中的数据是具有相似性的，而不同簇中的数据是不同的，当聚类完毕之后，我们就要分别去研究每个簇中的样本都有什么样的性质，从而根据业务需求来制定相应的策略。

  因此我们追求“簇内差异小，簇外差异大”。而这个“差异“，由样本点到其所在簇的质心的距离来衡量。

  对于一个簇来说，所有样本点到质心的距离之和越小，我们就认为这个簇中的样本越相似，簇内差异就越小。而距离的衡量方法有很多种，令x表示簇中的一个样本点，μ表示该簇中的质心，n表示每个样本点中的特征数目，i表示组成点x的每个特征，则该样本点到质心的距离可以由以下距离来度量：
$$欧几里得距离:d(x,\mu )=\sqrt{\sum _{i=1}^n(x_i-{\mu }_i{)}^2)}$$
$$曼哈顿距离:d(x,\mu )=\sum _{i=1}^n(|x_i-\mu |)$$

如我们采用欧几里得距离，则一个簇中所有样本点到质心的距离的平方和为：

$$ClusterSumofSquare（CSS）=\sum _{j=0}^m\sum _{i=1}^n(x_i-{\mu }_i{)}^2$$
$$TotalClusterSumofSquare=\sum _{l=1}^{k}CS{S}_i$$
  其中，m为一个簇中样本的个数，j是每个样本的编号。这个公式被称为簇内平方和，。而将一个数据集中的所有簇的簇内平方和相加，就得到了整体平方和。总体平方和越小，代表着每个簇内样本月相似，聚类的效果就越好。因此
KMeans追求的是，求解能够让Inertia最小化的质心。实际上，在质心不断变化不断迭代的过程中，总体平方和是越来越小的。我们可以使用数学来证明，当整体平方和最小的时候，质心就不再发生变化了。如此，K-Means的求解过程，就变成了一个最优化问题。

3.3 sklearn中的KMeans

class sklearn.cluster.KMeans(n_clusters=8, init=‘k-means++’, n_init=10, max_iter=300, tol=0.0001, precompute_distances=‘auto’, verbose=0, random_state=None, copy_x=True, n_jobs=1)

参数	含义
n_clusters	整数，可不填，默认为8
init	可输入“k-means++”,“random”或者一个n维数组 初始化质心的方法，默认为“k-means++”如果输入n维数组，数组的形状应该是(n_clusters,b_features)并给出初始质心
n_init	整数，默认10 使用不同的质心随机初始化的种子来运行kmeans算法的次数。最终结果会是基于inertia来计算的n_init次连续运行后的最佳输出
max_iter	整数，默认300 单次运行的k-means算法的最大迭代次数
tol	浮点数，默认1e-4 两次迭代间Inertia下降的量，如果两次迭代之间Inertia下降的值小于tol所设定的值，迭代就会停下
precompute_distances	‘auto’,True,False 默认为‘auto’ 预计算距离(更快但需要更多内存) ‘auto’:如果n_samples* n_clusters > 1200万，不要预先计算距离 True：始终预先计算距离 False：从不预先计算距离
random_state	整数，随机数或者None，默认None 确定质心初始化的随机数生成。使用int可以使随机性具有确定性

3.4 代码实现

引库

[1]:import pandas as pd
    import numpy as np
    import matplotlib.pyplot as plt

    from sklearn.cluster import KMeans

    from sklearn.datasets import make_blobs

创建数据集

[2]:X,y = make_blobs(n_samples=500,n_features=2,centers=4,random_state=1)

    fig,ax1 = plt.subplots(1)
    ax1.scatter(X[:,0],X[:,1]
                ,marker='o'
                ,s=8
               )
    plt.show()

训练模型

[3]:clusters=4
    model_kmeans = KMeans(n_clusters=clusters,random_state=1)
    cluster = model_kmeans.fit(X)

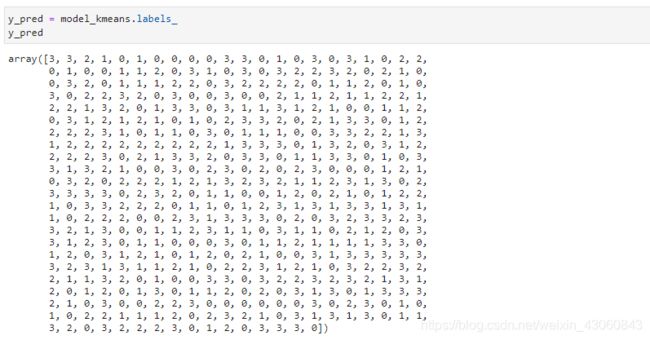
[4]:y_pred = model_kmeans.labels_
	y_pred 

查看质心

[5]:centroid = cluster.cluster_centers_
	centroid

array([[ -6.08459039,  -3.17305983],
       [ -1.54234022,   4.43517599],
       [-10.00969056,  -3.84944007],
       [ -7.09306648,  -8.10994454]])

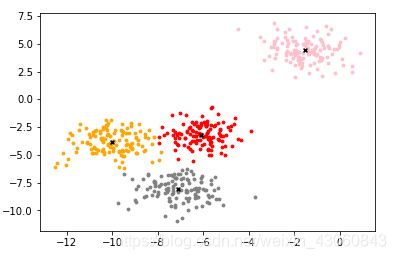
可视化

[6]:color = ["red","pink","orange","gray"]
	fig, ax1 = plt.subplots(1)
	for i in range(clusters):
   	 ax1.scatter(X[y_pred==i, 0], X[y_pred==i, 1]
           	,marker='o'
           	,s=8
           	,c=color[i]
           )
	ax1.scatter(centroid[:,0],centroid[:,1]
           ,marker="x"
           ,s=15
           ,c="black")
	plt.show()

3.5 聚类算法的模型评估指标

  不同于分类模型和回归，聚类算法的模型评估不是一件简单的事。在分类中，有直接结果（标签）的输出，并且分类的结果有正误之分，所以我们使用预测的准确度，混淆矩阵，ROC曲线等等指标来进行评估，但无论如何评估，都是在”模型找到正确答案“的能力。而回归中，由于要拟合数据，我们有SSE均方误差，有损失函数来衡量模型的拟合程度。但这些衡量指标都不能够使用于聚类。

  KMeans的目标是确保“簇内差异小，簇外差异大”，我们就可以通过衡量簇内差异来衡量聚类的效果。我们刚才说过，Inertia是用距离来衡量簇内差异的指标，因此，我们是否可以使用Inertia来作为聚类的衡量指标呢？

1. 为什么不用簇内距离平方和

  KMeans的目标是确保“簇内差异小，簇外差异大”，我们就可以通过衡量簇内差异来衡量聚类的效果。我们刚才说过，Inertia是用距离来衡量簇内差异的指标，因此，我们是否可以使用Inertia来作为聚类的衡量指标呢？Inertia越小模型越好嘛。

  可以，但是这个指标的缺点和极限太大

  首先，它不是有界的。我们只知道，Inertia是越小越好，是0最好，但我们不知道，一个较小的Inertia究竟有没有达到模型的极限，能否继续提高。

[7]:n_clusters = 5
	cluster_ = KMeans(n_clusters=n_clusters, random_state=0).fit(X)
	inertia_ = cluster_.inertia_
	inertia_

811.0952123653016

[8]:n_clusters = 6
	cluster_ = KMeans(n_clusters=n_clusters, random_state=0).fit(X)
	inertia_ = cluster_.inertia_
	inertia_

728.2827697678249

[8]:n_clusters = 10
	cluster_ = KMeans(n_clusters=n_clusters, random_state=0).fit(X)
	inertia_ = cluster_.inertia_
	inertia_

475.04707738309605

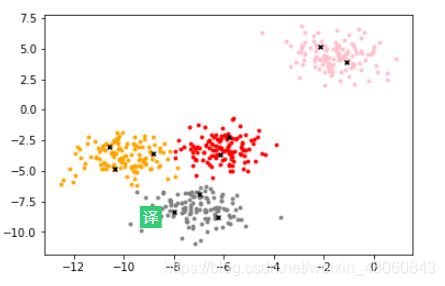
[9]:centroid = cluster_.cluster_centers_

	color = ["red","pink","orange","gray","red","pink","orange","gray","red","pink"]
	fig, ax1 = plt.subplots(1)
	for i in range(n_clusters):
    	ax1.scatter(X[y_pred==i, 0], X[y_pred==i, 1]
           ,marker='o'
           ,s=8
           ,c=color[i]
           )
	ax1.scatter(centroid[:,0],centroid[:,1]
           ,marker="x"
           ,s=15
           ,c="black")
	plt.show()

  第二，它的计算太容易受到特征数目的影响，数据维度很大的时候，Inertia的计算量会陷入维度诅咒之中，计算量会爆炸，不适合用来一次次评估模型。

  第三，它会受到超参数K的影响，在我们之前的常识中其实我们已经发现，随着K越大，Inertia注定会越来越小，但这并不代表模型的效果越来越好了

  第四，Inertia对数据的分布有假设，它假设数据满足凸分布（即数据在二维平面图像上看起来是一个凸函数的样子），并且它假设数据是各向同性的（isotropic），即是说数据的属性在不同方向上代表着相同的含义。但是现实中的数据往往不是这样。所以使用Inertia作为评估指标，会让聚类算法在一些细长簇，环形簇，或者不规则形状的流形时表现不佳

2. 轮廓系数

  在99%的情况下，我们是对没有真实标签的数据进行探索，也就是对不知道真正答案的数据进行聚类。这样的聚类，是完全依赖于评价簇内的稠密程度（簇内差异小）和簇间的离散程度（簇外差异大）来评估聚类的效果。其中轮廓系数是最常用的聚类算法的评价指标。它是对每个样本来定义的，它能够同时衡量：

1. 样本与其自身所在的簇中的其他样本的相似度a，等于样本与同一簇中所有其他点之间的平均距离

2. 样本与其他簇中的样本的相似度b，等于样本与下一个最近的簇中的所有点之间的平均距离

  根据聚类的要求”簇内差异小，簇外差异大“，我们希望b永远大于a，并且大得越多越好。

单个样本的轮廓系数计算为：
$$s=\frac{b-a}{max(a,b)}$$

  很容易理解轮廓系数范围是(-1,1)，其中值越接近1表示样本与自己所在的簇中的样本很相似，并且与其他簇中的样本不相似，当样本点与簇外的样本更相似的时候，轮廓系数就为负。当轮廓系数为0时，则代表两个簇中的样本相似度一致，两个簇本应该是一个簇。可以总结为轮廓系数越接近于1越好，负数则表示聚类效果非常差。

  如果一个簇中的大多数样本具有比较高的轮廓系数，则簇会有较高的总轮廓系数，则整个数据集的平均轮廓系数越高，则聚类是合适的。如果许多样本点具有低轮廓系数甚至负值，则聚类是不合适的，聚类的超参数K可能设定得太大或者太小。
  在sklearn中，我们使用模块metrics中的类silhouette_score来计算轮廓系数，它返回的是一个数据集中，所有样本的轮廓系数的均值。但我们还有同在metrics模块中的silhouette_sample，它的参数与轮廓系数一致，但返回的
是数据集中每个样本自己的轮廓系数。

我们来看看轮廓系数在我们自建的数据集上表现如何：

[10]:from sklearn.metrics import silhouette_score
	 from sklearn.metrics import silhouette_samples
[11]:silhouette_score(X,y_pred)

0.6505186632729437

[12]:silhouette_score(X,cluster_.labels_)

0.3356887273833359

  轮廓系数有很多优点，它在有限空间中取值，使得我们对模型的聚类效果有一个“参考”。并且，轮廓系数对数据的 分布没有假设，因此在很多数据集上都表现良好。但它在每个簇的分割比较清洗时表现好。但轮廓系数也有缺 陷，它在凸型的类上表现会虚高，比如基于密度进行的聚类，或通过DBSCAN获得的聚类结果，如果使用轮廓系数 来衡量，则会表现出比真实聚类效果更高的分数。
参考资料：机器学习实战
     菜菜的sklearn课堂