格密码学习笔记（一）

格密码学习笔记（一）

\qquad 随着当下量子计算机的研制的迅速进展，量子算法亦是相应得以巨大突破。在量子计算模型下，经典数论假设的密码体系（如大整数分解，计算有限域/椭圆曲线上的离散对数问题等），存在多项式时间（PPT）的量子算法，换而言之，经典数论密码体系受到了极大的冲击，将有可能成为旧时代的眼泪。因此，能够抵抗量子计算机攻击的密码——“后量子”或“抗量子”密码便应运而生。

\qquad 目前, 用于构建后量子密码系统的常见数学技巧包括：
1.杂凑函数,多变量方程(在构造签名方案时较有优势)
2.纠错码(更合适构造加密方案)
3.格(最通用的一类, 几乎所有经典密码概念都可以在格密码中实现)
4.超奇异椭圆曲线同源问题(当下较新的一类, 目前其中较受关注的有密钥交换和签名方案的构造,计算效率很低,还达不到实用性的要求)

一．格密码的基本概念：

I．根据向量空间的概念，格的定义如下:
\qquad 设$v_1,\dots ,v_n\in R^m,$为一组线性无关的向量。由$v_1,\dots ,v_n$生成的格$L$指的是向量$v_1,\dots ,v_n$的线性组合构成的向量集合，且其所使用的系数均在$Z^n$中，即
$L=\{a_1{v}_1+a_2{v}_2+\cdots +a_n{v}_n:a_1,a_2,\dots ,a_n\in Z\}$
\qquad 任意一组可以生成格的线性无关的向量都称为格的基，格的基中的向量个数称为格的维度。任意两组这样的向量中，向量的个数相同。
\qquad 某种程度上，格可以理解成系数为整数的向量空间。

II．与格相关的基本计算性难题：
1.SVP: Shortest Vector Problem （在格中寻找最短的非零向量）
\qquad 最短向量问题(SVP):在格$L$中寻找一个最短的非零向量，即寻找一个非零向量$v\in L$,使它的欧几里得范数$\Vert v\Vert$最小。

2.CVP: Closet Vector Problem（在格中寻找与指定非格向量最为接近的向量）
\qquad 最近向量问题(CVP):给定一个不在格$L$中的向量$w\in R^m$，寻找一个向量$v\in L$，使它最接近$w$ ，即寻找一个向量$v\in L$，使欧几里得范数$\Vert w-v\Vert$最小。

III.格密码简史：

时间	标志事件
18世纪–1982年	格经典数学问题的讨论，代表人物：Lagrange，Gues，Hermite，MInkowski等
1982年–1996年	期间标志性事件是LLL算法的提出（Lenstra-Lenstra-Lovasz）
1996年–2005年	第一代格密码诞生（Ajtai96, AD97G, GH9）
2005年–2016年	第二代格密码出现并逐步完善，并实用化格密码算法 （Regev05, GPV08,MP12 BLISS ,NewHope, Frodo）
2016年–	格密码逐步得以标准化

IV.格密码的发展大体分为两条主线：

从前		现在
具有悠久历史的格经典数学问题的研究	$⟹$	近30多年来高维格困难问题的求解算法及其计算复杂性理论研究
使用格困难问题的求解算法分析非格公钥密码体制的安全性	$⟹$	基于格困难问题的密码体制的设计

V．格密码优势：抗量子计算

格密码	经典密码
量子攻击算法	Shor算法
矩阵乘法、多项式乘法	Shor算法
Worst-case hardness	Average-case hardnes
结构灵活、功能丰富	结构简单、功能受限

VI .量子计算对经典密码算法的影响

密码算法	量子计算的影响
对称密码算法(SM4,AES)	密钥加倍（Grover）
散列函数(SM3,SHA-3)	输出长度增加（Grover）
经典公钥算法(RSA,DSA,ECC)	多项式算法（Shor）
格密码	未找到有效算法
多变量密码（数字签名）	未找到有效算法
基于Hash的密码（数字签名）	未找到有效算法
基于编码的密码（加密）	未找到有效算法
超奇异同源	未找到有效算法

二.LLL算法

\qquad LLL算法（Lenstra-Lenstra-Lovasz，lattice reduction）——以格规约（lattice）基数为输入，输出短正交向量基数。
\qquad 给定格$L$的一组基为 $\{v_1,v_2,\dots ,v_n\}$，然后对它进行约减。约减的主要目的是将这组任意给定的基转化为一组正交性较好的优质基，并使得这个优质基中的各个向量尽量最短。也就是说，首先要得到能够通过算法找到的最短向量，然后找到比这个最短向量稍长一点的向量，依次类推，直到最后找到这组基中的最后一个向量为止。或者，要使得在这个优质基中的向量之间具有相当好的正交性，即两个向量的点乘$v_i\cdot v_j$尽可能地接近于零。
I．基本概念
命题1 \quad 令$B=\{v_1,v_2,\dots ,v_n\}$为格$L$的一组基，且$B^{\ast }=\{v_1^{\ast },v_2^{\ast },\dots ,v_n^{\ast }\}$为相应的Gram-Schmidt正交基，则有$\det L=\prod _{i=1}^n\Vert v_i^{\ast }\Vert$。
定义1 \quad 令$V$表示一个向量空间啊， 是空间$W\subset V$的一个子空间， $W$在 $V$中的正交分量为 $W^{\perp }=\{v\in V:v\cdot w=0,\forall w\in W\}$。
定理1 \quad 令$L$表示一个维度为n的格，则$L$的任意一组LLL约减基$\{v_1，v_2,\dots ,v_n\}$具有如下两条性质：
$\prod _{i=1}^{\ast }\Vert v_i^{\ast }\Vert \le 2^{n(n-1)/4}\det L$
$\Vert v_j\Vert \le 2^{i-1}/2\Vert v_i^{\ast }\Vert ,\forall 1\le j\le i\le n$
\qquad 此外，LLL约减基的初始向量需满足
$\Vert v_1\Vert \le 2^{(n-1)/4}|\det L|$且$\Vert v_1\Vert \le 2^{(n-1)/2}\underset{0̸=v\in L}{\min }\Vert v\Vert$
\qquad 故一组LLL约减基能够以$2^{(n-1)/2}$系数解决apprSVP问题。
定理2（LLL算法） \quad 令$\{v_1,v_2,\dots ,v_n\}$为格$L$的一组基，则以下算法一定能够在有限步骤内终止，并且能够返回$L$的一组LLL约减基。

LLL算法
输入：格的一组基 $\{v_1,v_2,\dots ,v_n\}$
输出：LLL约减基
$1.$Input $\{v_1,v_2,\dots ,v_n\}$
$2.$Set $k=2$
$3.$ Set $v_i^{\ast }=v_j$
$4.$Loop while $k\le n$
$5.$Loop $j=1,2,3,\dots ,k-1$
$6.$Set $v_k=v_k-[{\mu }_{k,j}]v_j$（Size条件）
$7.$End $j$ Loop
$8.$if $\Vert v_k^{\ast }\Vert \ge (\frac{3}{4}-{\mu }_{k,k-1}^2)\Vert v_{k-1}^{\ast }{\Vert }^2$（Lovasz条件）
$9.$Set $k=k+1$
$10.$Else
$11.$Swap $v_{k-1}$ and $v_k$
$12.$Set $k=\max (k-1,2)$
$13.$End if
$14.$End $k$ Loop
$15.$Return LLL约减基 $\{v_1,v_2,\dots ,v_n\}$

注：每一步中，$v_1^{\ast },v_2^{\ast },\dots ,v_n^{\ast }$都是通过对当前向量$\{v_1,v_2,\dots ,v_n\}$值应用Gram-Schmidt正交化所得的正交向量集合，${\mu }_{i,j}$是相应$(v_i\cdot v_j)/\Vert v_j^{\ast }{\Vert }^2$的值。
\qquad LLL算法是一个多项式时间算法，在最多$O(n^2(\log n+\log (\max \Vert v_i\Vert )))$，LLL算法是一个多项式时间算法，在最多$O(n^6(\log (\max \Vert v_i\Vert ){)}^2)$次基本操作后终止。
定理3（LLL-apprCVP算法） \quad 存在一个常数 $C$，使得对于任意一个n维的格$L$ ，当给定一组基$\{v_1,v_2,\dots ,v_n\}$时，下面算法能够在 内解决apprCVP问题。

LLL-apprCVP算法
输入：格的一组基 $\{v_1,v_2,\dots ,v_n\}$，目标向量 $w$
输出：apprCVP问题的一个解 $v$
$1.$Set $k=2$
$2.$ Set $v_i^{\ast }=v_j$
$3.$Loop while $k\le n$
$4.$Loop $j=1,2,3,\dots ,k-1$
$5.$Set $v_k=v_k-[{\mu }_{k,j}]v_j$（Size条件）
$6.$End $j$ Loop
$7.$if $\Vert v_k^{\ast }\Vert \ge (\frac{3}{4}-{\mu }_{k,k-1}^2)\Vert v_{k-1}^{\ast }{\Vert }^2$（Lovasz条件）
$8.$Set $k=k+1$
$9.$Else
$10.$Swap $v_{k-1}$ and $v_k$
$11.$Set $k=\max (k-1,2)$
$12.$End if
$13.$End $k$ Loop
$14.$Result= LLL约减基 $\{v_1,v_2,\dots ,v_n\}$
$15.$Compute $w=t_1{v}_1+t_2{v}_2+\cdots +t_n{v}_n,t_1,t_2,\dots ,t_n\in R$
$16.$Loop $i=1,2,\dots ,n$
$17.$ $a_i=$round $(t_i)$
$18.$Return $a_1{v}_1+a_2{v}_2+\cdots +a_n{v}_n$

II．LLL算法MATLAB实现
1.计算Hadamard比率函数

计算Hadamard比率
输入：基向量作为行向量构成的方阵
输出：当前基的Hadamard比率
$1.$取出矩阵中的每个行向量
$2.$ 按照Hadamard比率公式进行计算
$3.$ 返回计算结果

function [result]=H(m)
% 计算一组基的Hadamard比率
n=size(m);
n=n(1);
product=1;
for i=1:n
    product=product*norm(m(i,:));
end
result=(abs(det(m))/product)^(1/n);
end

2.生成优质基函数

生成优质基
输入：向量中坐标的取值上限，基中向量的个数，Hadamard比率的下限
输出：矩阵形式的优质基
$1.$根据取值上限和指定维度，随机生成矩阵
$2.$调用LLL-apprCVP算法计算矩阵的Hadamard
$3.$ 若比率大于下限，则返回该矩阵；否则转回步骤1

function result=good_basis(N,v,h)
% 随机生成一组优质基
% N为基向量的坐标的绝对值上限；v为向量的
% 个数；h为Hadamard比率的下限
result=unidrnd(2*N,v)-N;
while H(result)

3.计算矩阵的行范数函数

计算矩阵的行范数
输入：矩阵形式的一组基
输出：一个包含了各个行向量范数的列向量
$1.$取出矩阵中的每个行向量
$2.$计算每个行向量的范数
$3.$ 返回计算结果

function [result]=row_norm(m)
%计算一个矩阵的行范数
n=size(m);
result=zores(n(1),1);
for i=1:n(1)
    result(i,1)=norm(m(i,:));
end
end

4.向量正交化函数

向量正交化
输入：矩阵形式的一组基
输出：正交化后的矩阵
\qquad\quad 具体步骤为Gram-Schmidt正交化算法步骤

function [M]=orthogonal(m)
% 使用Gram-Schmidt方法对矩阵，进行正交化（为单位化)
n=size(m);
M=zeros(n);
n=n(1);
M(1,:)=m(1,:);
for i=2:m
    M(i,:)=m(i,:);
    for j=1:i-1
        u_ij=dot(m(i,:))/(norm(M(j,:))^2);
        M(i,:)=M(i,:)-u_ij*M(j,:);
    end
end
end

5.LLL算法实现

格基约减
输入：矩阵形式的一组基
输出：经过一次约减后的基
\qquad\quad 具体步骤为LLL算法步骤

控制算法
输入：矩阵形式的一组基
输出：经过约减后的基
$1.$对于输入参数，调用格基约减算法
$2.$对上一步结果再次调用格基约减算法
$3.$ 重复步骤2，直到结果不再变化
$4.$ 返回最终结果

function [result]=LLL(v)
%使用LLL格基约减算法，对输入矩阵v进行处理
%其中v各行作为一行向量
%算法中多次调用基础过程，直到得到定值
a=lll(v);
b=lll(a);
while a~=b
    a=b;
    b=lll(b);
end
result=b
end

function [result]=lll(v)
%基础LLL格基约减过程
n=size(v);
n=n(1);

k=2
while k<=n
    V=orthogonal(v(1:k,:));
    for j=1:k-1
        u=dot(v(k,:),V(j,:))/norm(V(j,:)^2);
        v(k,:)=v(k,:)-round(u)*v(j,:);
    end
        %--------------------%
        u=dot(v(k,:),V(k-1,:))/(norm(V(k-1,:))^2);
        if norm(V(k,:))-2>=(3/4-u^2)*norm(V(k-1,:))^2
            k=k+1;
        else
            temp=v(k-1,:);
            v(k-1,:)=v(k,:);
            v(k,:)=temp;
            k=max(k-1,2);
        end
end
    result=v;
    return;
end

三.LWE（Learning With Errors）

\qquad 2005 年, Regev 提出了带错误的学习问题 (LWE), 证明了 LWE 与格上困难问题 (如近似最短向量问题 Gap-SVP) 相关, 并给出了基于 LWE 的公钥密码方案. 与之前出现的格上困难问题比较, LWE 在构建密码系统时更方便。
\qquad 给定矩阵$A\in Z_q^{m\times n}$和向量$b=As+e$，求解$s\in Z^n$。
\qquad 记为$L(A):=\{As:s\in Z_q^n\}+q{Z}^m$ 。

\qquad 其困难性来自方程的误差e
\qquad\qquad\quad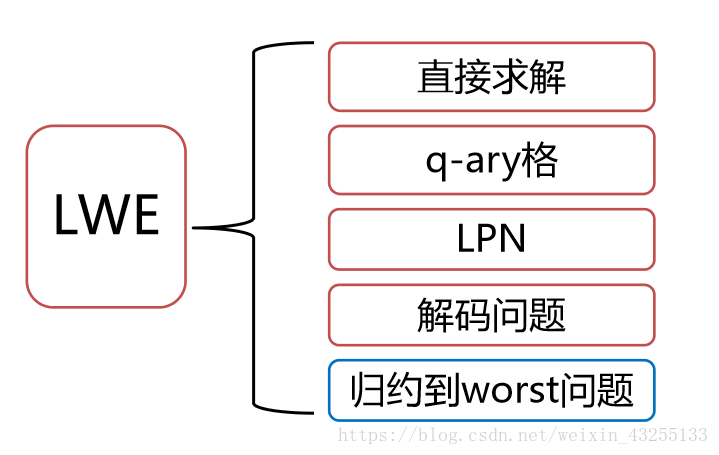
I.LWE的直观困难性

求解方法	方程	计算复杂度
直观求解之穷搜碰运气	$\{\begin{array}{l}\begin{array}{rl}⋮& \\ 1s_1+0s_2+0s_3& +0s_4\approx 8(\mathrm{m}\mathrm{o}\mathrm{d}17)\\ ⋮& \\ 1s_1+0s_2+0s_3& +0s_4\approx 7(\mathrm{m}\mathrm{o}\mathrm{d}17)\\ ⋮& \\ 1s_1+0s_2+0s_3& +0s_4\approx 8(\mathrm{m}\mathrm{o}\mathrm{d}17)\\ ⋮& \end{array}\end{array}$	计算复杂度：$O(2^{n\log q})$
直观求解之搜索s	{ 14 s 1 + 15 s 2 5 + 5 s 3 + 2 s 4 ≈ 8 ( m o d    17 ) 13 s 1 + 14 s 2 5 + 14 s 3 + 6 s 4 ≈ 16 ( m o d    17 ) 6 s 1 + 10 s 2 5 + 14 s 3 + 1 s 4 ≈ 3 ( m o d    17 ) 10 s 1 + 4 s 2 5 + 12 s 3 + 16 s 4 ≈ 12 ( m o d    17 ) 9 s 1 + 4 s 2 5 + 9 s 3 + 6 s 4 ≈ 9 ( m o d    17 ) 3 s 1 + 6 s 2 5 + 4 s 3 + 5 s 4 ≈ 16 ( m o d    17 ) 6 s 1 + 7 s 2 5 + 16 s 3 + 2 s 4 ≈ 3 ( m o d    17 ) \begin{cases}\begin{aligned}&14s_1+15s2_5+5s_3+2s_4\approx{8(\mod{17})}\\&13s_1+14s2_5+14s_3+6s_4\approx{16(\mod{17})}\\&6s_1+10s2_5+14s_3+1s_4\approx{3(\mod{17})}\\&10s_1+4s2_5+12s_3+16s_4\approx{12(\mod{17})}\\&9s_1+4s2_5+9s_3+6s_4\approx{9(\mod{17})}\\&3s_1+6s2_5+4s_3+5s_4\approx{16(\mod{17})}\\&6s_1+7s2_5+16s_3+2s_4\approx{3(\mod{17})}\end{aligned}\end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧​​14s1​+15s25​+5s3​+2s4​≈8(mod17)13s1​+14s25​+14s3​+6s4​≈16(mod17)6s1​+10s25​+14s3​+1s4​≈3(mod17)10s1​+4s25​+12s3​+16s4​≈12(mod17)9s1​+4s25​+9s3​+6s4​≈9(mod17)3s1​+6s25​+4s3​+5s4​≈16(mod17)6s1​+7s25​+16s3​+2s4​≈3(mod17)​​	计算复杂度：$O(2^{n\log q})$
直观求解之BKW03	$\{\begin{array}{l}\begin{array}{rlr}14s_1+15s{2}_5& ⋮+5s_3+⋮2s_4\approx 8(\mathrm{m}\mathrm{o}\mathrm{d}17)& \\ 13s_1+14s{2}_5& ⋮+14s_3+⋮6s_4\approx 16(\mathrm{m}\mathrm{o}\mathrm{d}17)& \\ 6s_1+10s{2}_5& ⋮+14s_3+⋮1s_4\approx 3(\mathrm{m}\mathrm{o}\mathrm{d}17)& \\ 10s_1+4s{2}_5& ⋮+12s_3+⋮16s_4\approx 12(\mathrm{m}\mathrm{o}\mathrm{d}17)& \\ 9s_1+4s{2}_5& ⋮+9s_3+⋮6s_4\approx 9(\mathrm{m}\mathrm{o}\mathrm{d}17)& \\ 3s_1+6s{2}_5& ⋮+4s_3+⋮5s_4\approx 16(\mathrm{m}\mathrm{o}\mathrm{d}17)& \\ 6s_1+7s{2}_5& ⋮+16s_3+⋮2s_4\approx 3(\mathrm{m}\mathrm{o}\mathrm{d}17)& \end{array}\end{array}$	计算复杂度：$O(2^n)$
q-ary格	$\begin{array}{rl}& L(A):=\{A^t:s\in Z_q^n\}+q{Z}^m\\ & L^{\perp }(A):=\{z\in Z^m:A_Z=0\in Z_q^n\}\\ & ⟨A,⟨z,⟨As+e⟩⟩⟩=⟨A,z⟩\end{array}$	LLL计算随机q-ary格的短基

II．LWE的困难性归约 Worst to Averag
1.困难问题与LWE归约关系

SIVP	GapSVP	出处
$O(\alpha /n)$	$O(\alpha /n)$	Regev，2005年，首次提出LWE问题并通过量子算法将困难问题规约到LWE，需要 $\alpha p>2\sqrt{n}$
$\omega [\frac{n\log n}{\alpha (n)}]$	$O(n/\alpha (n))$	Pekert，2009年，通过离散高斯测度（DGS）得到，两个归约都需要量子算法，此结果适用于 $p\in [2,\infty )$
	$O(n/\alpha \sqrt{\log n})$	Peikert, 2009年，首次去量子化，在概率多项式时间内归约，其中 $\alpha \in (0,1),q\ge \frac{\zeta }{n}\cdot \omega (\sqrt{\log n}),q\ge 2^{\frac{n}{2}}$
$O(\sqrt{k}\cdot q)$		Micciancio，peikert，2013年，对应 $LWE(m,n,q)$,其中 $0<k\le n\le m-\omega (\log k)\le k^{\alpha (1)},q\le k^{\alpha (1)}$，此结果证明了当误差分布足够小（0-1）时LWE是困难的
$O(\sqrt{n})$	$O(\sqrt{n})$	Brakerski，Peikert等，2013年，与Peikert，09相比，将模数 $q$缩小到了 $ploy(n)$

2.困难问题归约关系
\qquad\qquad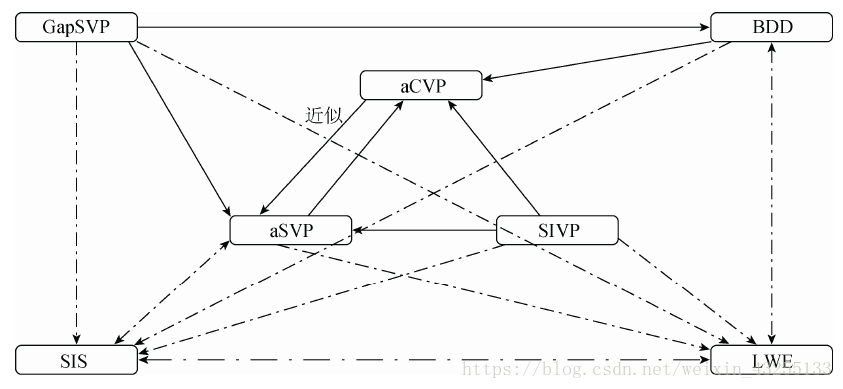
注：
1.当选择合适的参数 $n,m,q,{\chi }_s,{\chi }_e$ 时, 搜索型 LWE 问题的难解性与格上困难问题相关。
2.使用量子技术将 LWE 问题的平均情形困难性和随机格上 GapSVP$\gamma$和 SIVP$\gamma$ 问题的最坏情形 困难性联系起来, 其中参数 γ 的选取与 LWE 问题的参数相关。
3.在选取合适的参数时, 判定型 LWE 问题和搜索型 LWE 问题是多项式等价的。

定义1（近似最短向量问题（aSVP））给定$Z^n$中秩为$d$的格$L$的一组基$B$和一个近似参数$\gamma \ge 1$，如何寻找到一个非零向量$u\in L$，使得满足$\Vert u\Vert \le \underset{v\in L}{\min }\Vert v\Vert$或$\Vert u\Vert \le \gamma {\lambda }_1$.

定义2（近似最短向量问题对应判断性问题（GapSVP））给定$Z^n$中秩为$d$的格$L$的一组基$B$，实数$r$和一个近似参数$\gamma \ge 1$。当${\lambda }_1(L(B))\le r$时判定为“YES”，当${\lambda }_1(L(B))\ge \gamma r$时判定为“NO”，如果$r\le {\lambda }_1(L(B))\le \gamma r$时判定为“YES”或“NO”均可。

定义3（近似最近向量问题（aCVP））给定$Z^n$中秩为$d$的格$L$的一组基$B$，一个目标向量$x\in span(L)$（ $x$不必在格位上）和一个近似参数$\gamma \ge 1$，如何寻找到一个向量$u\in L$，使得满足$\Vert u-x\Vert =dist(x,L)$。

定义4（近似最近向量问题对应判断性问题（GapCVP））给定$Z^n$中秩为$d$的格$L$的一组基$B$，一个目标向量$x\in span(L)$（$x$不必在格位上）和一个近似参数$\gamma \ge 1$。当$dist(x,L)\le r$时判定为“YES”，当$dist(x,L)\ge \gamma r$时判定为“NO”，如果$r\le dist(x,L)\le \gamma r$时判定为“YES”或“NO”均可。

定义5（小整数问题（SIS））给定模数$q/ge1$，常实数$v$和矩阵$A\in Z_q^{n\times m}$ ，其中$m\ge n>0$。如何寻找一个非零向量$u\in Z^m$，使得$Au=0\mathrm{m}\mathrm{o}\mathrm{d}q$且$\Vert u\Vert \le v$。

定义6（搜索型误差学习（LWE））给定一个维数$n\ge 1$，模数$q\ge 1$，$Z_q$上一概率分布$\chi$和$A_{s,\chi }$上任意多个抽样，如何确定$s$。

定义7（误差学习判定问题（LWE））给定一个维数$n\ge 1$，模数$q\ge 1$，$Z_q$ 上一概率分布$\chi$。随机从分布$Z_q^n\times Z_q$中均匀抽样或$A_{s,\chi }$中独立抽样，如果判断此抽样来自$A_{s,\chi }$则返回“YES”，如果来自$Z_q^n\times Z_q$，则返回“NO”。

定义8（有界距离译码（BDD））给定$Z^n$中秩为$d$的格$L$的一组基$B$，一个距离参数$\alpha >0$和一个目标向量$x\in span(L)$（$x$不必在格位上），其中$dist(x,L)<\alpha {\lambda }_1(L)$，如何寻找到一个向量$x\in L$，使得满足$\Vert u-x\Vert =dist(x,L)$。

定义9（最短独立向量问题（SIVP））给定$Z^n$中秩为$d$的格$L$的一组基$B$和一个近似参数$\gamma \ge 1$，如何寻找到一个非零向量$u_1,u_2,\dots ,u_d\in L$，使得满足$\underset{i=1,2,\dots ,d}{\max }\Vert u_i\Vert =\gamma {\lambda }_d(L)$。

四.小结

I.大势所趋：
（1）量子密码理论——信息安全领域“军备竞赛”：
（2）各界对于后量子密码系统的实装需求迫切, 预计接下来未来几年将是实用化后量子密码学快速发展时期；
II．我们可以尝试接触的格密码相关方向：
（1）格理论和算法设计；（2）LWE密码方案设计；（3）全同态密码。