计算机视觉ch4 标定手机相机参数

在拍摄中，相机有可能会出现畸变，我们需要用软件对拍摄的照片进行校正，避免出现桶形或枕形畸变

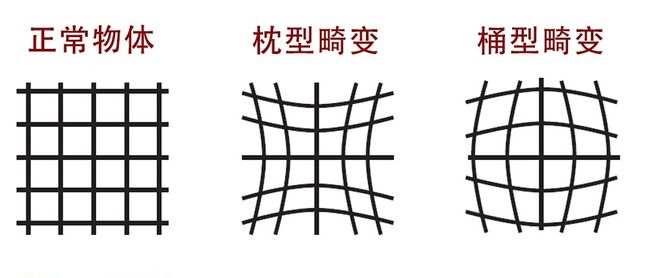
不同的镜头的在生产和组装过程中的畸变程度各不相同，通过相机标定可以校正这种镜头畸变，生成矫正后的图像

原理

一般来说，标定的过程分为两个部分：

1. 从世界坐标系转换为相机坐标系，这一步是三维点到三维点的转换，包括 R，t （相机外参）等参数
2. 从相机坐标系转为图像坐标系，这一步是三维点到二维点的转换，包括 K（相机内参）等参数
   世界坐标系转换为相机坐标系
   
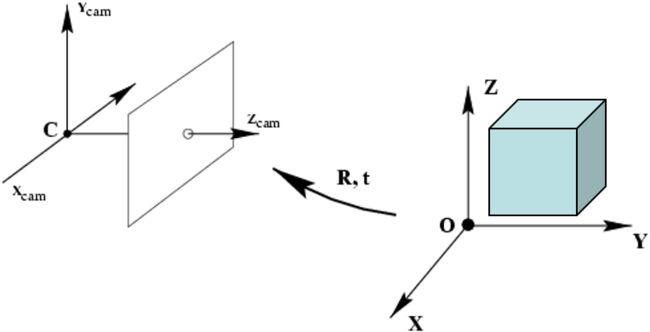
   公式如下：
   
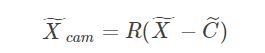
   相机坐标系转换为图像坐标系
   
   

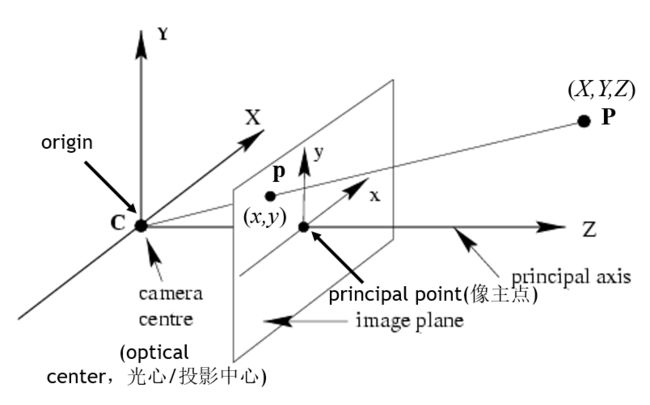
相机内参数矩阵

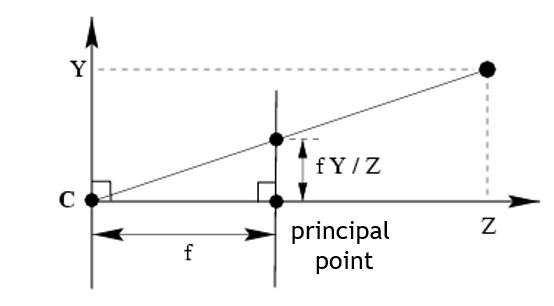
设P=(X,Y,Z)P=(X,Y,Z)为场景中的一点，在针孔相机模型中，其要经过以下几个变换，最终变为二维图像上的像点p=(μ,ν)p=(μ,ν):

1. 将PP从世界坐标系通过刚体变换(旋转和平移)变换到相机坐标系，这个变换过程使用的是相机间的相对位姿，也就是相机的外参数。
2. 从相机坐标系，通过透视投影变换到相机的成像平面上的像点p=(x,y)p=(x,y)。
3. 将像点pp从成像坐标系，通过缩放和平移变换到像素坐标系上点p=(μ,ν)p=(μ,ν)。

相机将场景中的三维点变换为图像中的二维点，也就是各个坐标系变换的组合，可将上面的变换过程整理为矩阵相乘的形式：

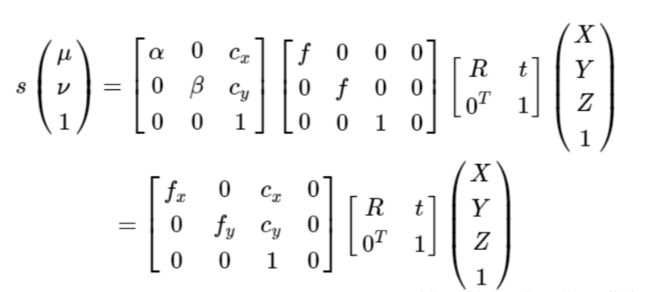
矩阵K称为相机的内参数矩阵

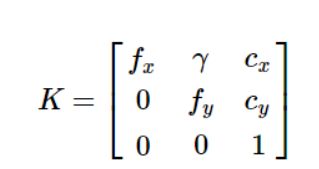
张正友标定法

使用棋盘格标定的方法，将照片中的三维信息压缩为二维（Z=0)
在张氏标定法中，用于标定的棋盘格是三维场景中的一个平面Π，其在成像平面的像是另一个平面π，知道了两个平面的对应点的坐标，就可以求解得到两个平面的单应矩阵H。其中，标定的棋盘格是特制的，其角点的坐标是已知的；图像中的角点，可以通过角点提取算法得到（如Harris角点），这样就可以得到棋盘平面Π和图像平面π的单应矩阵H。
具体步骤如下：

1. 检测每张图片中的棋盘图案的角点
2. 利用解析解估算方法计算出5个内部参数，以及6个外部参数
3. 通过基于极大似然准则的优化解,提高A，R，t矩阵的精度

棋盘平面和成像平面间的单应

将一个平面映射到另一个平面，将棋盘格所在的平面映射到相机的成像平面，则有

设棋盘格所在的平面为世界坐标系中Z=0Z=0的平面，这样棋盘格的任一角点PP的世界坐标为(X,Y,0)(X,Y,0)，根据小孔相机模型：

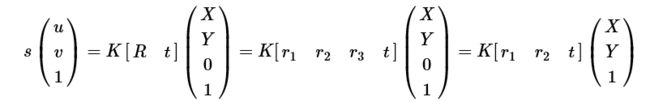
根据平面间的单应性，有

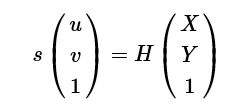
将上面两个等式进行整合，则可以得到单应矩阵HH和相机矩阵（包含内参和外参）的相等，如下：

这样就可以使用棋盘平面和成像平面间的单应矩阵来约束相机的内参和外参。单应矩阵HH可以通过棋盘平和成像平面上对应的点计算出来。

Python代码实现

生成灰度图

import cv2
#循环灰度图片并保存
def grayImg():
    for x in range(1,13):
        #读取图片
        img = cv2.imread("E:\Program Files (x86)\PyCharm Community Edition 2019.1.2\
        code\pcv-book-code-master\ch04\pic\{}.jpg".format(str(x)))
        GrayImage=cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
        GrayImage=cv2.resize(GrayImage,(1000,1333))
        #保存灰度后的新图片
        cv2.imwrite("E:\Program Files (x86)\PyCharm Community Edition 2019.1.2\
        code\pcv-book-code-master\ch04\pic\data\{}.jpg".format(str(x)),GrayImage)

grayImg()

相机标定

# !usr/bin/env/ python
# _*_ coding:utf-8 _*_
import cv2 as cv
import numpy as np
import os
from step.homography import get_homography
from step.intrinsics import get_intrinsics_param
from step.extrinsics import get_extrinsics_param
from step.distortion import get_distortion
from step.refine_all import refinall_all_param

def calibrate():
    # 求单应矩阵
    H = get_homography(pic_points, real_points_x_y)

    # 求内参
    intrinsics_param = get_intrinsics_param(H)

    # 求对应每幅图外参
    extrinsics_param = get_extrinsics_param(H, intrinsics_param)

    # 畸变矫正
    k = get_distortion(intrinsics_param, extrinsics_param, pic_points, real_points_x_y)

    # 微调所有参数
    [new_intrinsics_param, new_k, new_extrinsics_param] = refinall_all_param(intrinsics_param,
    k, extrinsics_param, real_points,pic_points)

    print("intrinsics_parm:\t", new_intrinsics_param)
    print("distortionk:\t", new_k)
    print("extrinsics_parm:\t", new_extrinsics_param)

if __name__ == "__main__":
    file_dir = r'..\pic\data'
    # 标定所用图像
    pic_name = os.listdir(file_dir)
    # 由于棋盘为二维平面，设定世界坐标系在棋盘上，一个单位代表一个棋盘宽度，产生世界坐标系三维坐标
    cross_corners = [9, 5]  # 棋盘方块交界点排列
    real_coor = np.zeros((cross_corners[0] * cross_corners[1], 3), np.float32)
    real_coor[:, :2] = np.mgrid[0:9, 0:5].T.reshape(-1, 2)
    real_points = []
    real_points_x_y = []
    pic_points = []
    for pic in pic_name:
        pic_path = os.path.join(file_dir, pic)
        pic_data = cv.imread(pic_path)
        # 寻找到棋盘角点
        succ, pic_coor = cv.findChessboardCorners(pic_data, (cross_corners[0], cross_corners[1]), None)
        if succ:
            # 添加每幅图的对应3D-2D坐标
            pic_coor = pic_coor.reshape(-1, 2)
            pic_points.append(pic_coor)
            real_points.append(real_coor)
            real_points_x_y.append(real_coor[:, :2])
    calibrate()

结果