计算视觉——图像分割

目录

最大流最小割

最大流

最小割

图割（Graph Cut）

从图像创建图

---

最大流最小割

最大流

最大流就是从起点到终点所能达到的最高单位流量。为了下文表示上的方便，将容量、最大流都给出一个形式化的定义：

                                              

最大流计算方法：

通路：从图起点（S）到达图结束点（T）的路径，由一系列顶点组成；

通路流量：该通路上所能达到的最大单位流量；

饱和边：容量等于通路流量的有向边。

具体算法描述：

Step1：初始化最大流Flow=0；

Step2：在图中找一条通路，如果通路不存在，则结束；

Step3：Flow = Flow+通路流量；

Step4：对通路上所有边的容量进行更新 Cij = Cij-通路流量；

Step5：跳转Step2

注意：在上述算法中，当容量为0时，代表该边已经无效，不能作为通路路经中的边。

算法的有效性解读：

这里使用了解读，而没有使用证明，也就表示以下说法是从一种直观的角度来描述，不是严谨的推理证明。算法是有效的，因为当图中已经没有通路的时候，已经不可能再增加图的流量，所以至少已经达到了本次计算过程中的最大流。剩下的另一部份就是如何来说明通路选择的顺序与最终计算的最大流结果无关？如果两条通路之间是独立的，那么先选择的通路不会对后选择的通路产生影响。如果两条通路并非独立，那么也是可以简单证明通路的先后选择与这两条通路上的最大流无关。如果两条通路的可以被证明，那么将两条通路看作一条通路，证明N+1情况下同样成立。

最小割

一个割就是一组边的集合，将给集合边从图中边集合中移除，那么图被分割为两个部分，这两个部分之间没有任何边连接。如果说得有点绕口，那么最简单来说，一块肉被从中间隔开，分成两个部分，中间断开的连接的集合就是割。

最小割就是将图切割为两个部分时，代价最小的割的集合，代价就是边上容量的和（S部分到T部分边的容量）。还是拿猪肉作类比，最小割就是找到一块肉连接最小的部分，一刀劈开，那个部分的连接就是最小割。

如何找到这个最小割？

当一个图被割分成两个部分时，不再存在S到T的通路，所以割的代价必定大于等于图的最大流（这个需要添加额外说明吗？应该不需要吧，算是非常明显的结论了吧）。那么也就是说，割的代码最小不能小于图的最大流，也就是割的代价等于图的最大流。

现在确定了割的代价，但如何去找到这样一组割？在进行具体算法说明之前，给出额外一个概念：

影响边：在计算最大流的算法中，会对边的容量进行修改，而将一条通路中修改后容量为0的边称为修改后容量非0边的影响边；

算法描述：

Step1： 初始化边影响边集合；

Step2： 初始化最小割边集合；

Step3： 记录边的原始容量Rij=Cij；

Step3： 寻找一个通路，如果没有通路，则结束；

Step4： 修正边的容量Cij = Cij-通路流量；

Step5： 在通路的边中找一个Cij=0的边，作为预切割边；

Step6： 如果预切割边的容量等于该边的原始容量（Cij=Rij），那么将该边加入最小割边集合；否则，找到该边的所有影响边，将影响边从最小割边集合中移出，将该边加入最小割边集合；

Step7： 对通路其他边记录影响边；

算法的有效性解读：

算法的核心原理就是在寻找最大流的过程中，找出一组边代价等于最大流，并且能够将遍历的通路有效分割的边。

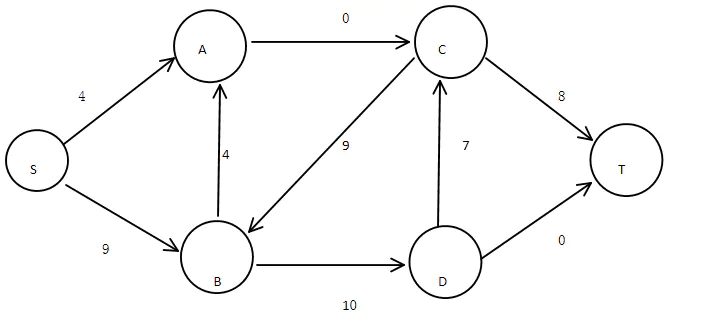
在上图中，我们要寻找第一个通路

红色字体表示该通路的通路流量。根据算法进行容量修正：

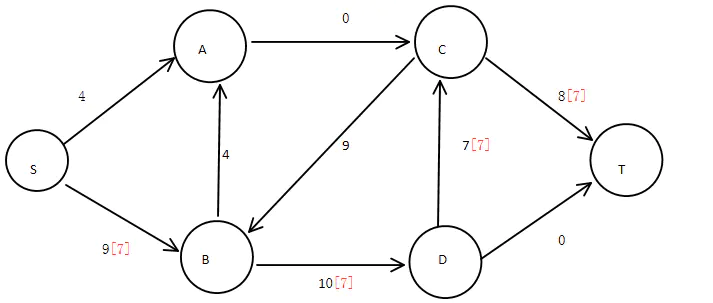
修改后的容量是用红色字体表示。在此通路中，AC边容量为0，所以将该边加入最小割边集合{AC}，同时记录影响边信息，SA的影响边{AC},CT的影响边{AC}。

寻找第二条通路：

 

 

此时，最小割边集合为{AC，DT}

寻找第三条通路：

 

此时最小割边集合为：{AC，DT，DC}

此时，已经不再存在通路，所以当前最小割边集合就是求解的最小割，其代价为23。

图割（Graph Cut）

图像分割是将一幅图像分割成有意义区域的过程。区域可以是图像的前景与背景或图像中一些单独的对象。这些区域可以利用一些诸如颜色、边界或近邻相似性等特征进行构建。

1、基于阈值的分割方法

      阈值法的基本思想是基于图像的灰度特征来计算一个或多个灰度阈值，并将图像中每个像素的灰度值与阈值相比较，最后将像素根据比较结果分到合适的类别中。因此，该类方法最为关键的一步就是按照某个准则函数来求解最佳灰度阈值。

2、基于边缘的分割方法

       所谓边缘是指图像中两个不同区域的边界线上连续的像素点的集合，是图像局部特征不连续性的反映，体现了灰度、颜色、纹理等图像特性的突变。通常情况下，基于边缘的分割方法指的是基于灰度值的边缘检测，它是建立在边缘灰度值会呈现出阶跃型或屋顶型变化这一观测基础上的方法。

阶跃型边缘两边像素点的灰度值存在着明显的差异，而屋顶型边缘则位于灰度值上升或下降的转折处。正是基于这一特性，可以使用微分算子进行边缘检测，即使用一阶导数的极值与二阶导数的过零点来确定边缘，具体实现时可以使用图像与模板进行卷积来完成。

3、基于区域的分割方法

      此类方法是将图像按照相似性准则分成不同的区域，主要包括种子区域生长法、区域分裂合并法和分水岭法等几种类型。

       种子区域生长法是从一组代表不同生长区域的种子像素开始，接下来将种子像素邻域里符合条件的像素合并到种子像素所代表的生长区域中，并将新添加的像素作为新的种子像素继续合并过程，直到找不到符合条件的新像素为止。该方法的关键是选择合适的初始种子像素以及合理的生长准则。

        区域分裂合并法（Gonzalez，2002）的基本思想是首先将图像任意分成若干互不相交的区域，然后再按照相关准则对这些区域进行分裂或者合并从而完成分割任务，该方法既适用于灰度图像分割也适用于纹理图像分割。

        分水岭法（Meyer，1990）是一种基于拓扑理论的数学形态学的分割方法，其基本思想是把图像看作是测地学上的拓扑地貌，图像中每一点像素的灰度值表示该点的海拔高度，每一个局部极小值及其影响区域称为集水盆，而集水盆的边界则形成分水岭。该算法的实现可以模拟成洪水淹没的过程，图像的最低点首先被淹没，然后水逐渐淹没整个山谷。当水位到达一定高度的时候将会溢出，这时在水溢出的地方修建堤坝，重复这个过程直到整个图像上的点全部被淹没，这时所建立的一系列堤坝就成为分开各个盆地的分水岭。分水岭算法对微弱的边缘有着良好的响应，但图像中的噪声会使分水岭算法产生过分割的现象。

4、基于图论的分割方法

        此类方法把图像分割问题与图的最小割（min cut）问题相关联。首先将图像映射为带权无向图G=，图中每个节点N∈V对应于图像中的每个像素，每条边∈E连接着一对相邻的像素，边的权值表示了相邻像素之间在灰度、颜色或纹理方面的非负相似度。而对图像的一个分割s就是对图的一个剪切，被分割的每个区域C∈S对应着图中的一个子图。而分割的最优原则就是使划分后的子图在内部保持相似度最大，而子图之间的相似度保持最小。基于图论的分割方法的本质就是移除特定的边，将图划分为若干子图从而实现分割。目前所了解到的基于图论的方法有GraphCut，GrabCut和Random Walk等。

5、基于能量泛函的分割方法

       该类方法主要指的是活动轮廓模型（active contour model）以及在其基础上发展出来的算法，其基本思想是使用连续曲线来表达目标边缘，并定义一个能量泛函使得其自变量包括边缘曲线，因此分割过程就转变为求解能量泛函的最小值的过程，一般可通过求解函数对应的欧拉(Euler．Lagrange)方程来实现，能量达到最小时的曲线位置就是目标的轮廓所在。按照模型中曲线表达形式的不同，活动轮廓模型可以分为两大类：参数活动轮廓模型（parametric active contour model）和几何活动轮廓模型（geometric active contour model）。

       参数活动轮廓模型是基于Lagrange框架，直接以曲线的参数化形式来表达曲线，最具代表性的是由Kasset a1(1987)所提出的Snake模型。该类模型在早期的生物图像分割领域得到了成功的应用，但其存在着分割结果受初始轮廓的设置影响较大以及难以处理曲线拓扑结构变化等缺点，此外其能量泛函只依赖于曲线参数的选择，与物体的几何形状无关，这也限制了其进一步的应用。

       几何活动轮廓模型的曲线运动过程是基于曲线的几何度量参数而非曲线的表达参数，因此可以较好地处理拓扑结构的变化，并可以解决参数活动轮廓模型难以解决的问题。而水平集（Level Set）方法（Osher，1988）的引入，则极大地推动了几何活动轮廓模型的发展，因此几何活动轮廓模型一般也可被称为水平集方法。

Graph cuts是一种十分有用和流行的能量优化算法，在计算机视觉领域普遍应用于前背景分割（Image segmentation）、立体视觉（stereo vision）、抠图（Image matting）等。

此类方法把图像分割问题与图的最小割（min cut）问题相关联。首先用一个无向图G=表示要分割的图像，V和E分别是顶点（vertex）和边（edge）的集合。此处的Graph和普通的Graph稍有不同。普通的图由顶点和边构成，如果边的有方向的，这样的图被则称为有向图，否则为无向图，且边是有权值的，不同的边可以有不同的权值，分别代表不同的物理意义。而Graph Cuts图是在普通图的基础上多了2个顶点，这2个顶点分别用符号”S”和”T”表示，统称为终端顶点。其它所有的顶点都必须和这2个顶点相连形成边集合中的一部分。所以Graph Cuts中有两种顶点，也有两种边。

第一种顶点和边是：第一种普通顶点对应于图像中的每个像素。每两个邻域顶点（对应于图像中每两个邻域像素）的连接就是一条边。这种边也叫n-links。

第二种顶点和边是：除图像像素外，还有另外两个终端顶点，叫S（source：源点，取源头之意）和T（sink：汇点，取汇聚之意）。每个普通顶点和这2个终端顶点之间都有连接，组成第二种边。这种边也叫t-links。

上图就是一个图像对应的s-t图，每个像素对应图中的一个相应顶点，另外还有s和t两个顶点。上图有两种边，实线的边表示每两个邻域普通顶点连接的边n-links，虚线的边表示每个普通顶点与s和t连接的边t-links。在前后景分割中，s一般表示前景目标，t一般表示背景。

图中每条边都有一个非负的权值we，也可以理解为cost（代价或者费用）。一个cut（割）就是图中边集合E的一个子集C，那这个割的cost（表示为|C|）就是边子集C的所有边的权值的总和。

Graph Cuts中的Cuts是指这样一个边的集合，很显然这些边集合包括了上面2种边，该集合中所有边的断开会导致残留”S”和”T”图的分开，所以就称为“割”。如果一个割，它的边的所有权值之和最小，那么这个就称为最小割，也就是图割的结果。而福特-富克森定理表明，网路的最大流max flow与最小割min cut相等。所以由Boykov和Kolmogorov发明的max-flow/min-cut算法就可以用来获得s-t图的最小割。这个最小割把图的顶点划分为两个不相交的子集S和T，其中s ∈S，t∈ T和S∪T=V 。这两个子集就对应于图像的前景像素集和背景像素集，那就相当于完成了图像分割。

        也就是说图中边的权值就决定了最后的分割结果，那么这些边的权值怎么确定呢？

       图像分割可以看成pixel labeling（像素标记）问题，目标（s-node）的label设为1，背景（t-node）的label设为0，这个过程可以通过最小化图割来最小化能量函数得到。那很明显，发生在目标和背景的边界处的cut就是我们想要的（相当于把图像中背景和目标连接的地方割开，那就相当于把其分割了）。同时，这时候能量也应该是最小的。假设整幅图像的标签label（每个像素的label）为L= {l1,l2,,,, lp }，其中li为0（背景）或者1（目标）。那假设图像的分割为L时，图像的能量可以表示为：

E(L)=aR(L)+B(L)

       其中，R(L)为区域项（regional term），B(L)为边界项（boundary term），而a就是区域项和边界项之间的重要因子，决定它们对能量的影响大小。如果a为0，那么就只考虑边界因素，不考虑区域因素。E(L)表示的是权值，即损失函数，也叫能量函数，图割的目标就是优化能量函数使其值达到最小。

区域项：

，其中Rp(lp)表示为像素p分配标签lp的惩罚，Rp(lp)能量项的权值可以通过比较像素p的灰度和给定的目标和前景的灰度直方图来获得，换句话说就是像素p属于标签lp的概率，我希望像素p分配为其概率最大的标签lp，这时候我们希望能量最小，所以一般取概率的负对数值，故t-link的权值如下：

Rp(1) = -ln Pr(Ip|’obj’)； Rp(0) = -ln Pr(Ip|’bkg’)

        由上面两个公式可以看到，当像素p的灰度值属于目标的概率Pr(Ip|’obj’)大于背景Pr(Ip|’bkg’)，那么Rp(1)就小于Rp(0)，也就是说当像素p更有可能属于目标时，将p归类为目标就会使能量R(L)小。那么，如果全部的像素都被正确划分为目标或者背景，那么这时候能量就是最小的。

边界项：

 

        其中，p和q为邻域像素，边界平滑项主要体现分割L的边界属性，B可以解析为像素p和q之间不连续的惩罚，一般来说如果p和q越相似（例如它们的灰度），那么B越大，如果他们非常不同，那么B就接近于0。换句话说，如果两邻域像素差别很小，那么它属于同一个目标或者同一背景的可能性就很大，如果他们的差别很大，那说明这两个像素很有可能处于目标和背景的边缘部分，则被分割开的可能性比较大，所以当两邻域像素差别越大，B越小，即能量越小。

        好了，现在我们来总结一下：我们目标是将一幅图像分为目标和背景两个不相交的部分，我们运用图分割技术来实现。首先，图由顶点和边来组成，边有权值。那我们需要构建一个图，这个图有两类顶点，两类边和两类权值。普通顶点由图像每个像素组成，然后每两个邻域像素之间存在一条边，它的权值由上面说的“边界平滑能量项”来决定。还有两个终端顶点s（目标）和t（背景），每个普通顶点和s都存在连接，也就是边，边的权值由“区域能量项”Rp(1)来决定，每个普通顶点和t连接的边的权值由“区域能量项”Rp(0)来决定。这样所有边的权值就可以确定了，也就是图就确定了。这时候，就可以通过min cut算法来找到最小的割，这个min cut就是权值和最小的边的集合，这些边的断开恰好可以使目标和背景被分割开，也就是min cut对应于能量的最小化。而min cut和图的max flow是等效的，故可以通过max flow算法来找到s-t图的min cut。目前的算法主要有：

1) Goldberg-Tarjan

2) Ford-Fulkerson

3) 上诉两种方法的改进算法

 

权值：

Graph cut的3x3图像分割示意图：我们取两个种子点（就是人为的指定分别属于目标和背景的两个像素点），然后我们建立一个图，图中边的粗细表示对应权值的大小，然后找到权值和最小的边的组合，也就是（c）中的cut，即完成了图像分割的功能。

 

图论中的图是由若干节点（有时也称顶点）和连接节点的边构成的集合。

 

图中，边可以是有向的或无向的，并且这些可能有与它们相关联的权重。

图割是一个有向图分割成两个互不相交的集合，可以用来解决很多计算机视觉方面的问题，诸如立体深度重建、图像拼接和图像分割等计算视觉方面的不同问题。从图像像素和学生的近邻创建一个图并引入一个能量或“代价”函数，我们有可能利用图割方法将图像分割成两个或多个区域。图像分割的基本思想是，相似且彼此相近的像素应该分到同一区域。

图像分割的思想是用图来表示图像，并对图进行划分以使割代价以使割代价最小。在用图表示图像时，增加两个额外的节点，即源点和汇点；并仅考虑那些将源点和汇点分开的割。

寻找最小割等同于在源点和汇点间寻找最大流，此外，很多有效的算法都可以解决这些最大流/最小割问题。

 

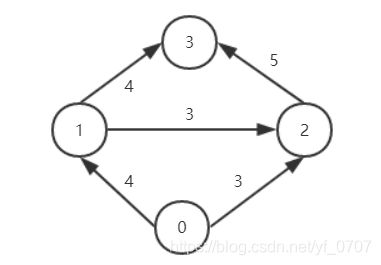
我们在图割例子中将采用python-graph工具包，该工具包包含了许多非常有用的图算法。

from pygraph.classes.digraph import digraph
from pygraph.algorithms.minmax import maximum_flow

gr = digraph()
gr.add_nodes([0,1,2,3])
gr.add_edge((0,1), wt=4)
gr.add_edge((1,2), wt=3)
gr.add_edge((2,3), wt=5)
gr.add_edge((0,2), wt=3)
gr.add_edge((1,3), wt=4)
flows,cuts = maximum_flow(gr, 0, 3)
print ('flow is:' , flows)
print ('cut is:' , cuts)

上述函数，我们用到maximum_flow()函数，该函数用Edmonds-Karp算法计算最大流/最小割，采用一个完全用python写成工具包的好处是安装兼容性好，不足是速度较慢。代码中，首先创建有4个节点的有向图，4个节点的索引分别是0,1,2,3,然后用add_edge()增添边并为每条边指定特定的权重。边的权重用来衡量边的最大流容量。以节点0为源点，3为汇点，计算最大流。打印出流和割结果：

 

从图像创建图

给定一个邻域结构，我们可以利用图像像素作为节点定义一个图。这里集中讨论最简单的像素四邻域和两个图像区域（前景和背景）情况。一个四邻域指一个像素与其正上方、正下方、左边、右边的像素直接相连。处了像素节点外，我们需要两个特定的节点——“源”点和“汇”点，来分别代表图像的前景和背景。

创建一个这样的图的步骤：

• 每个像素节点都有一个从源点的传入边；
• 每个像素节点都有一个到汇点的传出边；
• 每个像素节点都有一条传入边连接到它的近邻。

为确定边的权重，需要一个能够确定这些像素点之间，像素点与源点、汇点之间边的权重（表示那条边的最大流）的分割模型。我们可以为边的权重建立如下模型：

利用该模型，可以将每个像素和前景及背景（源点和汇点）连接起来，权重等于上面归一化后的概率。描述了近邻间像素的相似性，相似像素权重趋近于k，不相似的趋近于0.参数表征了随着不相似性的增加，指数次幂衰减到0的快慢。

from pylab import *
from numpy import *

from pygraph.classes.digraph import digraph
from pygraph.algorithms.minmax import maximum_flow

from PCV.classifiers import bayes

""" 
Graph Cut image segmentation using max-flow/min-cut. 
"""

def build_bayes_graph(im,labels,sigma=1e2,kappa=1):
    """    Build a graph from 4-neighborhood of pixels. 
        Foreground and background is determined from
        labels (1 for foreground, -1 for background, 0 otherwise) 
        and is modeled with naive Bayes classifiers.
        """
   """ 从像素四邻域建立一个图，前景和背景（前景用 1 标记，背景用 -1 标记，    其他的用 0 标记）由 labels 决定，并用朴素贝叶斯分类器建模 """  
    m,n = im.shape[:2]
    
    # RGB vector version (one pixel per row)
    # 每行是一个像素的 RGB 向量 
    vim = im.reshape((-1,3))
    
    # RGB for foreground and background
    # 前景和背景（RGB）
    foreground = im[labels==1].reshape((-1,3))
    background = im[labels==-1].reshape((-1,3))    
    train_data = [foreground,background]
    
    # train naive Bayes classifier
    # 训练朴素贝叶斯分类器 
    bc = bayes.BayesClassifier()
    bc.train(train_data)

    # get probabilities for all pixels
    # 获取所有像素的概率 
    bc_lables,prob = bc.classify(vim)
    prob_fg = prob[0]
    prob_bg = prob[1]
    
    # create graph with m*n+2 nodes
    # 用m * n +2 个节点创建图 除所有像素点外加上原点和汇点
    gr = digraph()
    gr.add_nodes(range(m*n+2))
    
    source = m*n # second to last is source
    sink = m*n+1 # last node is sink

    # normalize
    # 归一化 
    for i in range(vim.shape[0]):
        vim[i] = vim[i] / (linalg.norm(vim[i]) + 1e-9)
    
    # go through all nodes and add edges
    # 遍历所有的节点，并添加边 
    for i in range(m*n):
        # add edge from source
        # 从源点添加边 
        gr.add_edge((source,i), wt=(prob_fg[i]/(prob_fg[i]+prob_bg[i])))
        
        # add edge to sink
        # 向汇点添加边 
        gr.add_edge((i,sink), wt=(prob_bg[i]/(prob_fg[i]+prob_bg[i])))
        
        # add edges to neighbors
        # 向相邻节点添加边
        
        if i%n != 0: # left exists # 左边存在
            edge_wt = kappa*exp(-1.0*sum((vim[i]-vim[i-1])**2)/sigma)
            gr.add_edge((i,i-1), wt=edge_wt)
        if (i+1)%n != 0: # right exists
            edge_wt = kappa*exp(-1.0*sum((vim[i]-vim[i+1])**2)/sigma)
            gr.add_edge((i,i+1), wt=edge_wt)
        if i//n != 0: # up exists
            edge_wt = kappa*exp(-1.0*sum((vim[i]-vim[i-n])**2)/sigma)
            gr.add_edge((i,i-n), wt=edge_wt)
        if i//n != m-1: # down exists
            edge_wt = kappa*exp(-1.0*sum((vim[i]-vim[i+n])**2)/sigma)
            gr.add_edge((i,i+n), wt=edge_wt)
        
    return gr    
        
    
def cut_graph(gr,imsize):
    """    Solve max flow of graph gr and return binary 
        labels of the resulting segmentation."""
      """ 用最大流对图 gr 进行分割，并返回分割结果的二值标记 """ 
      
    m,n = imsize
    source = m*n # second to last is source # 倒数第二个节点是源点 
    sink = m*n+1 # last is sink# 倒数第已个节点是汇点 
    
    # cut the graph
    # 对图进行分割
    flows,cuts = maximum_flow(gr,source,sink)
    
    # convert graph to image with labels
     # 将图转为带有标记的图像
    res = zeros(m*n)
    for pos,label in list(cuts.items())[:-2]: #don't add source/sink  # 不要添加源点 / 汇点 
        res[pos] = label

    return res.reshape((m,n))
    
    
def save_as_pdf(gr,filename,show_weights=False):

    from pygraph.readwrite.dot import write
    import gv
    dot = write(gr, weighted=show_weights)
    gvv = gv.readstring(dot)
    gv.layout(gvv,'fdp')
    gv.render(gvv,'pdf',filename)


def show_labeling(im,labels):
    """    Show image with foreground and background areas.
        labels = 1 for foreground, -1 for background, 0 otherwise."""
    
    imshow(im)
    contour(labels,[-0.5,0.5])
    contourf(labels,[-1,-0.5],colors='b',alpha=0.25)
    contourf(labels,[0.5,1],colors='r',alpha=0.25)
    #axis('off')
    xticks([])
    yticks([])

 

# -*- coding: utf-8 -*-

from scipy.misc import imresize
from PCV.tools import graphcut
from PIL import Image
from numpy import *
from pylab import *

im = array(Image.open("empire.jpg"))
im = imresize(im, 0.07)
size = im.shape[:2]

# add two rectangular training regions
labels = zeros(size)
labels[3:18, 3:18] = -1
labels[-18:-3, -18:-3] = 1

# create graph
g = graphcut.build_bayes_graph(im, labels, kappa=1)

# cut the graph
res = graphcut.cut_graph(g, size)
  
figure()
graphcut.show_labeling(im, labels)

figure()
imshow(res)
gray()
axis('off')

show()

放入的图片：

 

运行结果：

 

不同参数下的结果：

g = graphcut.build_bayes_graph(im,labels,kappa=1)

变量Kappa（方程中的K）决定了近邻像素间边的相对权重。改变K值分割的效果如下图所示，随着K值增大，分割边界将变得更平滑，并且细节部分也逐步丢失。你可以根据自己应用的需要及想要获得的结果类型来选择合适的K值。