图数据结构解析(翻译 Graph Data Structures for Beginners)
英文原文地址
在本博客中我们将会探索非线性数据结构——图。本博客内容将讲解图的主要结构以及其典型应用。
您可能正在使用有关图形(和树)的程序。 比方说,您想知道自己工作的地方和家庭之间的最短路径,那么您可以使用图算法来获得答案! 接下来我们将探讨这个并且涉及一些其他有趣的挑战。
1.图基础(Graphs Basics)
图是一种数据结构,其中节点可以具有零个或多个相邻元素。两个节点之间的连接称为边。 节点也可以称为顶点。
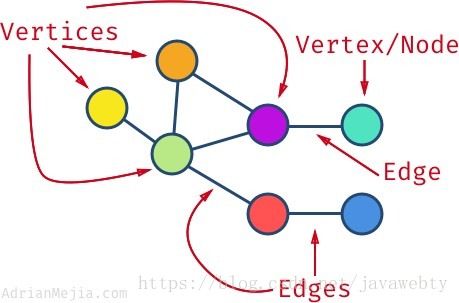
度数是连接到顶点的边数。 例如,紫色顶点的度数为3,而蓝色顶点的度数为1。
如果边是双向的(无方向箭头),那么我们有一个无向图。 但是,如果边有方向,那么我们有一个有向图或简图。 您可以将其视为单行道(定向)或双向道路(无定向)。
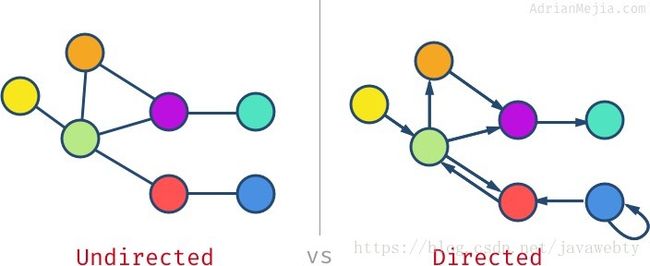
顶点可以具有自身的边(例如,蓝色节点),这称为自循环。
图形可以具有循环,这意味着如果遍历节点,则可以多次访问同一节点。 没有循环的图形称为非循环图形。
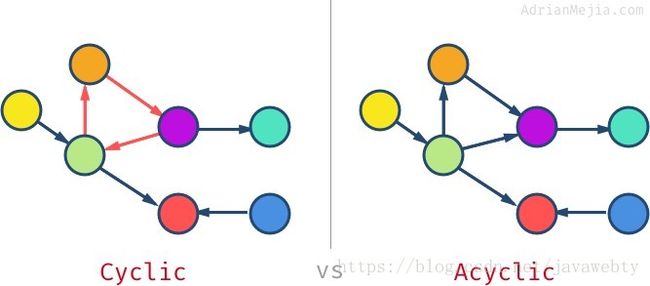
并非所有顶点都必须在图中连接。 您可能有孤立的节点甚至是分离的子图。 如果所有节点都有至少一个边,那么我们有一个连通图。 当所有节点都连接到所有其他节点时,我们就有了一个完整的图形。

对于完整的图,每个节点必须对其他节点有1个边。 在前面的例子中,我们有7个顶点,因此每个节点有6个边。
2.图形应用(Graph Applications)
当边具有分配给它们的值/成本时,我们说我们有一个加权图。 如果没有重量,我们可以假设它是1。

加权图具有许多应用程序,具体取决于您需要解决问题的域。 仅举几例:
航空交通(上图)
节点/顶点=机场
边=两个机场之间的直达航班
权重=两个机场之间的英里数
GPS导航
节点 =道路切断
边=道路
权重 =从一个交叉路口到另一个交叉路口所需的时间
网络路由
节点 =服务器
边 =数据链接
权重=连接速度
通常,图表有许多真实的应用程序,如:
电子电路
航班预订
行车路线
社交网络:例如,Facebook使用图表来推荐朋友
建议:亚马逊/ Netflix使用图表来制作产品/电影的建议
图表帮助后勤规划交付货物的物流方案
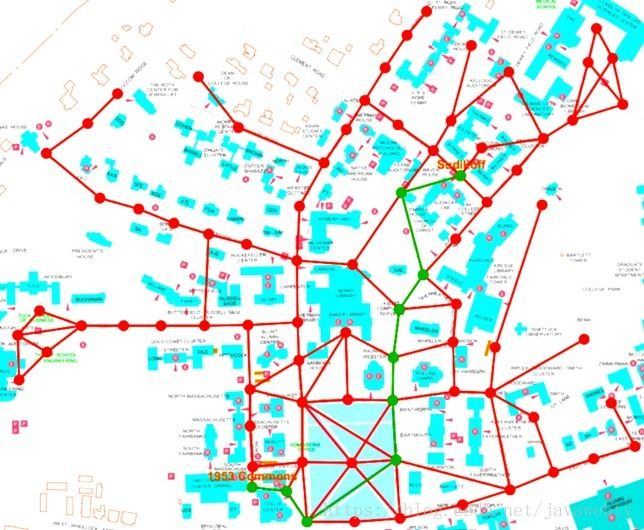
我们刚刚学习了图形和一些应用程序的基础知识。 现在让我们学习如何在代码中表示图形。
3.图的表示(Representing graphs)
图表有两种主要方式:
1.邻接表
2.邻接矩阵
让我们用以下有向图(有向图)作为例子来解释它:

我们有4个节点的有向图。 当顶点具有到其自身的链接(例如a)时,称为自循环。
- 3.1 邻接矩阵 (Adjacency Matrix)
邻接矩阵是使用二维阵列(N×N矩阵)表示图的一种方式。 在节点的交集中,如果它们是连接的,我们加1(或其他权重),如果它们没有连接,则用0或 -表示 。
a b c d e
a 1 1 - - -
b - - 1 - -
c - - - 1 -
d - 1 1 - -
如您所见,矩阵水平和垂直列出所有节点。 如果有几个连接我们称为稀疏图,如果有很多连接(接近最大链接数),我们称之为密集图。 如果达到所有可能的连接,那么我们有一个完整的图表。
重要的是要注意,对于无向图,邻接矩阵将始终由对角线对称。 然而,对于有向图(例如我们的例子)并非总是如此。
找到两个顶点连接的时间复杂度是多少?
查询两个节点是否在邻接矩阵中连接是O(1)。空间复杂性?
将图存储为邻接矩阵的空间复杂度为O(n^2),其中n是顶点数。 可另外表示为O(V^2)添加顶点的时间
顶点存储为VxV矩阵。 因此,每次添加顶点时,矩阵都需要重建为(V + 1)x(V + 1)。则邻接矩阵上添加顶点是O(V^2)如何获取一个节点的相邻节点?
由于矩阵具有VxV矩阵,为了使所有相邻节点到达给定顶点,我们必须转到节点行并获得其余节点的所有边缘。
在我们前面的例子中,假设我们希望所有相邻节点都是b。 我们必须得到b与所有其他节点的完整行。
a b c d e
b - - 1 - -
我们必须访问所有节点。
在邻接矩阵上获取相邻节点是O(| V |) o(n)想象一下,如果您需要将Facebook网络表示为图形。 你将不得不创建一个20亿x20亿的矩阵,其中大部分都是空的! 没有人会知道所有人,一个人知道的最多只有几千人。
通常,稀疏图如果用矩阵表示会浪费大量空间。 这就是为什么在大多数实现中我们会使用邻接列表而不是矩阵。
- 3.2邻接列表(Adjacency List)
邻接列表是表示图形的最常用方法之一。 每个节点都有一个连接到它的所有节点的列表集合。
可以使用包含节点的Array(或HashMap)作为邻接列表的数据结构。 每个节点条目列出其相邻节点的列表(可以通过阵列,链表,集等进行存储)。
例如,在上图中,我们知道a与b有连接,并且自身也有自我循环。 反过来,b与c有连接,依此类推:
a -> { a b }
b -> { c }
c -> { d }
d -> { b c }
如您所想,如果您想知道节点是否连接到另一个节点,则必须浏览该列表。
查询邻接列表中两个节点是否相互连接,时间复杂度为O(n),其中n是顶点数。 也表示为O(V)空间复杂性?
将图存储为邻接列表的空间复杂度为O(n),其中n是顶点和边的总和。 另外,表示为O(V + E)4.邻接列表图HashMap实现
邻接列表是表示图形的最常用方式。 有几种方法可以实现邻接列表:
其中一个最简单的方法是使用HashMap。 key表示节点,value表示节点连接的节点的数组集合。
const graph = {
a: ['a', 'b'],
b: ['c'],
c: ['d'],
d: ['b', 'c']
}图表通常需要以下操作:
添加和删除顶点
添加和删除边
添加和删除顶点涉及更新邻接列表。
假设我们想要删除顶点b。 我们可以删除graph ['b'];但是,我们仍然要删除d和a上邻接列表中的引用。
每次我们删除一个节点时,我们都必须遍历所有节点的列表O(V + E )。 可以做得更好吗? 稍后我们将回答这个问题,首先让我们以更加面向对象的方式实现我们的列表,这样我们就可以轻松地交换实现。
5.操作实现
让我们从保存顶点值及其相邻顶点的Node类开始。 我们还可以使用辅助函数来添加和删除列表中的相邻节点。
class Node {
constructor(value) {
this.value = value;
this.adjacents = []; // adjacency list
}
addAdjacent(node) {
this.adjacents.push(node);
}
removeAdjacent(node) {
const index = this.adjacents.indexOf(node);
if(index > -1) {
this.adjacents.splice(index, 1);
return node;
}
}
getAdjacents() {
return this.adjacents;
}
isAdjacent(node) {
return this.adjacents.indexOf(node) > -1;
}
}请注意,添加该节点连接节点的时间复杂度为O(1),而删除其中一个相邻节点时间复杂度为O(E)。 如果使用HashSet而不是数组怎么办? 它可能是O(1)。 但是,首先让它工作,然后我们可以让它更快。
好了,现在我们有了Node类,让我们构建一个Graph类,它可以执行添加/删除顶点和边等操作。
Graph.constructor
class Graph {
constructor(edgeDirection = Graph.DIRECTED) {
this.nodes = new Map();
this.edgeDirection = edgeDirection;
}
// ...
}
Graph.UNDIRECTED = Symbol('directed graph'); // one-way edges
Graph.DIRECTED = Symbol('undirected graph'); // two-ways edges
我们需要知道的第一件事是图表是指向还是未指向,这会影响我们添加边时候的操作。(未指向则两个节点的数组中都要加上对方节点,而有对象的则不需要)
Graph.addVertex
我们创建节点的方式是将它添加到nodes Map中。 映射存储键/值对,其中key是顶点的值,而映射值是Node类的实例(上面的Node类)
addVertex(value) {
if(this.nodes.has(value)) {
return this.nodes.get(value);
} else {
const vertex = new Node(value);
this.nodes.set(value, vertex);
return vertex;
}
}Graph.addEdge
添加边,我们需要两个节点。 一个是来源,另一个是目的地。
addEdge(source, destination) {
const sourceNode = this.addVertex(source);
const destinationNode = this.addVertex(destination);
sourceNode.addAdjacent(destinationNode);
if(this.edgeDirection === Graph.UNDIRECTED) {
destinationNode.addAdjacent(sourceNode);
}
return [sourceNode, destinationNode];
}我们从源顶点到目标添加边。 如果我们有一个无向图,那么我们也会从目标节点添加到源,因为它是双向的。
从图形邻接列表添加边的运行时间为:O(1)Graph.removeVertex
从图中删除节点,它涉及的更多一点。 我们必须检查要删除的节点是否存在别的节点连接数组里面
removeVertex(value) {
const current = this.nodes.get(value);
if(current) {
for (const node of this.nodes.values()) {
node.removeAdjacent(current);
}
}
return this.nodes.delete(value);
}我们必须遍历每个节点然后每个节点的每个相邻的节点(边)。
从图形邻接列表中删除顶点的运行时间为:O(| V | + | E |)Graph.removeEdge
删除边缘非常简单,与addEdge类似。
removeEdge(source, destination) {
const sourceNode = this.nodes.get(source);
const destinationNode = this.nodes.get(destination);
if(sourceNode && destinationNode) {
sourceNode.removeAdjacent(destinationNode);
if(this.edgeDirection === Graph.UNDIRECTED) {
destinationNode.removeAdjacent(sourceNode);
}
}
return [sourceNode, destinationNode];
}addEdge和removeEdge之间的主要区别在于:
- 如果顶点不存在,我们将不会创建它们。
由于removeAdjacent必须遍历所有相邻顶点,因此我们有以下运行时:
O(|E|)6.广度优先搜索(BFS) - 图搜索
广度优先搜索是一种从初始一个节点开始访问所有其他节点的图数据导航方式
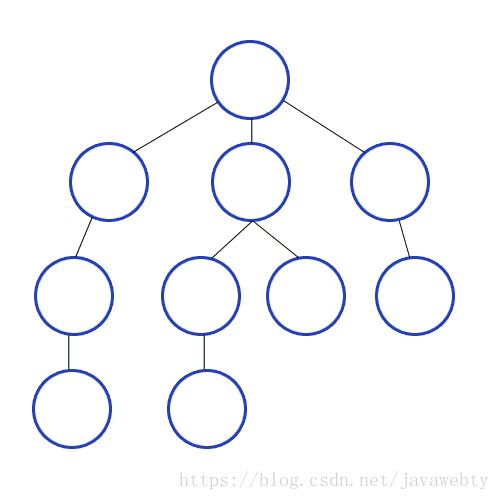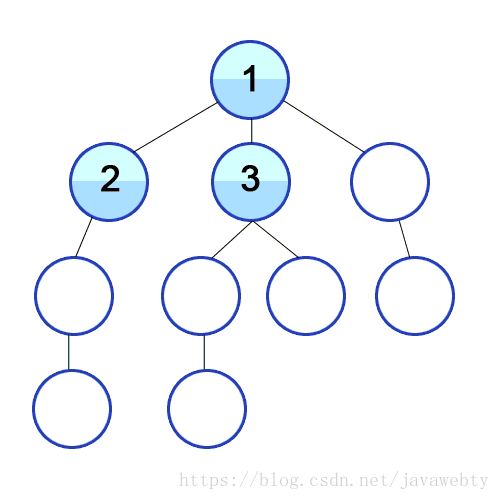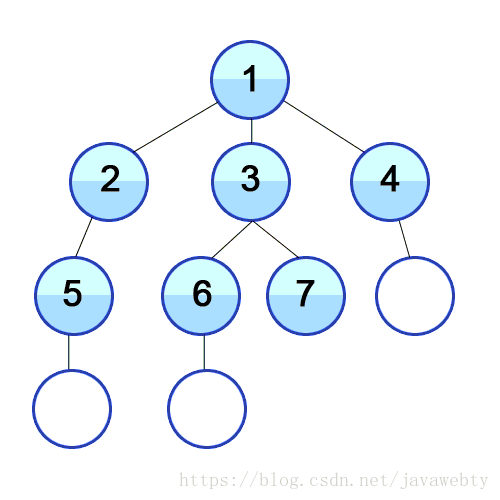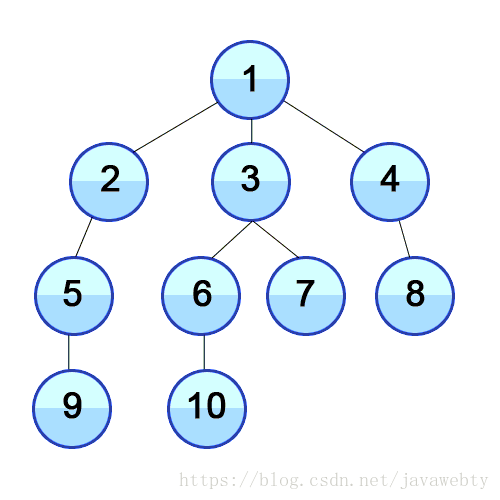
让我们看看我们如何在代码中实现这一目标:
*bfs(first) {
const visited = new Map();
const visitList = new Queue();
visitList.add(first);
while(!visitList.isEmpty()) {
const node = visitList.remove();
if(node && !visited.has(node)) {
yield node;
visited.set(node);
node.getAdjacents().forEach(adj => visitList.add(adj));
}
}
}如您所见,我们正在使用队列,其中第一个节点也是第一个要访问的节点(FIFO)。
我们也使用JavaScript生成器,注意函数前面的*。 我们使用生成器一次迭代一个值。 这对大型图形(数百万个节点)很有用,因为在大多数情况下,您不需要访问每个节点。
这是一个如何使用我们刚刚创建的BFS的示例:
const graph = new Graph(Graph.UNDIRECTED);
const [first] = graph.addEdge(1, 2);
graph.addEdge(1, 3);
graph.addEdge(1, 4);
graph.addEdge(5, 2);
graph.addEdge(6, 3);
graph.addEdge(7, 3);
graph.addEdge(8, 4);
graph.addEdge(9, 5);
graph.addEdge(10, 6);
bfsFromFirst = graph.bfs(first);
bfsFromFirst.next().value.value; // 1
bfsFromFirst.next().value.value; // 2
bfsFromFirst.next().value.value; // 3
bfsFromFirst.next().value.value; // 47.深度优先搜索(DFS) - 图搜索
深度优先搜索是递归从初始节点开始找到的每个节点来进行图数据导航的方式。

*dfs(first) {
const visited = new Map();
const visitList = new Stack();
visitList.add(first);
while(!visitList.isEmpty()) {
const node = visitList.remove();
if(node && !visited.has(node)) {
yield node;
visited.set(node);
node.getAdjacents().forEach(adj => visitList.add(adj));
}
}这边是有栈(FILO)
例子:
const graph = new Graph(Graph.UNDIRECTED);
const [first] = graph.addEdge(1, 2);
graph.addEdge(1, 3);
graph.addEdge(1, 4);
graph.addEdge(5, 2);
graph.addEdge(6, 3);
graph.addEdge(7, 3);
graph.addEdge(8, 4);
graph.addEdge(9, 5);
graph.addEdge(10, 6);
dfsFromFirst = graph.dfs(first);
visitedOrder = Array.from(dfsFromFirst);
const values = visitedOrder.map(node => node.value);
console.log(values); // [1, 4, 8, 3, 7, 6, 10, 2, 5, 9]
正如您所看到的,BFS和DFS上的图表是相同的,但是,访问节点的顺序是非常不同的。 BFS按顺序从1到10,而DFS在每个节点上尽可能深。