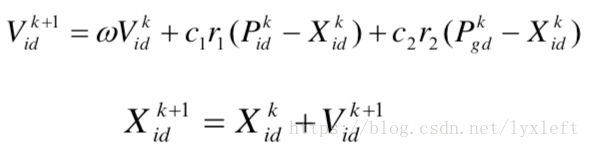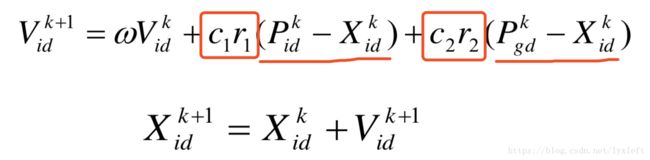粒子群优化算法（PSO）简介及MATLAB实现

目录

粒子群优化算法概述

PSO算法步骤

PSO（粒子群优化算法）与GA（遗传算法）对比

PSO的MATLAB实现

---

粒子群优化算法概述

• 粒子群优化(PSO, particle swarm optimization)算法是计算智能领域，除了蚁群算法，鱼群算法之外的一种群体智能的优化算法，该算法最早由Kennedy和Eberhart在1995年提出的，该算法源自对鸟类捕食问题的研究。

• PSO算法首先在可行解空间中初始化一群粒子，每个粒子都代表极值优化问题的一个潜在最优解，用位置、速度和适应度值三项指标表示该粒子特征。

• 粒子在解空间中运动，通过跟踪个体极值Pbest和群体极值Gbest更新个体位置，个体极值Pbest是指个体所经历位置中计算得到的适应度值最优位置，群体极值Gbest是指种群中的所有粒子搜索到的适应度最优位置。

• 粒子每更新一次位置，就计算一次适应度值，并且通过比较新粒子的适应度值和个体极值、群体极值的适应度值更新个体极值Pbest和群体极值Gbest位置。

在每一次迭代过程中，粒子通过个体极值和群体极值更新自身的速度和位置，更新公式如下:

上式中V是速度，以当前的速度加上两个修正项：该个体与当前行进路径中最优个体的差距、与群体最优值的偏差。c1和c2是系数，r1、r2是随机数。

X是位置，用当前位置加上速度。根据相邻时间间隔默认为一个时间单位，故速度和距离可以直接相加。

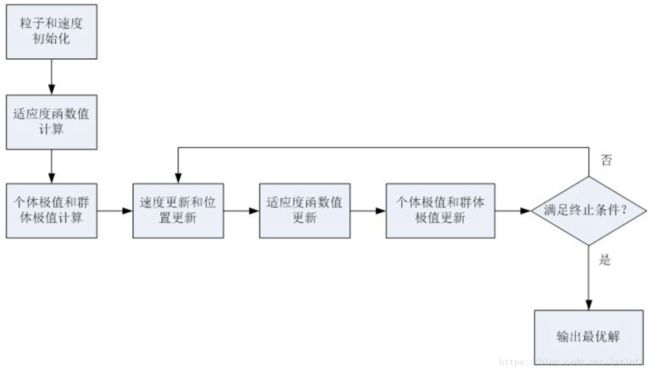
PSO算法步骤

步骤中的关键点提示：

1）初始化、适应度函数计算和遗传算法很相似。

2）群体极值是好找的。但个体极值：第一步时，每个个体的值都是个体极值，第二步后才开始有真正的个体极值的概念。

3）终止条件：比如说，达到多少次迭代次数，相邻两次误差小于一定值，等等。也可以多种终止条件混合使用。

PSO（粒子群优化算法）与GA（遗传算法）对比

• 相同点:

1）种群随机初始化，上面也提到了。

2）适应度函数值与目标最优解之间：都有一个映射关系

• 不同点:

1）PSO算法没有选择、交叉、变异等操作算子。取而代之的是个体极值、群体极值来实现逐步优化的功能。GA的相关操作含义参见《遗传算法原理简介及其MATLAB实践》。

2）PSO有记忆的功能：

在优化过程中参考到了上一步的极值情况（划横线的部分）。按此公式计算出新的粒子位置时，若新粒子的适应度函数还不如之前的好，则这个优化方法会帮助优化进程回到之前的位置，体现了一个记忆的效果。矩形内是权重系数。

3）信息共享机制不同，遗传算法是互相共享信息，整个种群的移动是比较均匀地向最优区域移动，而在PSO中，只有gBest或lBest给出信息给其他粒子，属于单向的信息流动，整个搜索更新过程是跟随当前最优解的过程。因此， 在一般情况下，PSO的收敛速度更快。

简单直白地理解：GA在变异过程中可能从比较好的情况又变成不好的情况，不是持续收敛的过程，所以耗时会更长些。

PSO的MATLAB实现

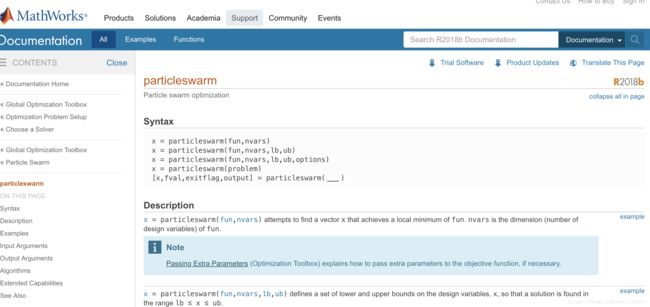
MATLAB2014以上有自带的PSO的工具箱函数。

这里我们自己写代码来实现一下PSO：

【例】利用PSO寻找极值点：y = sin(10*pi*x) / x;

%% I. 清空环境
clc
clear all

%% II. 绘制目标函数曲线图
x = 1:0.01:2;
y = sin(10*pi*x) ./ x;
figure
plot(x, y)
hold on

%% III. 参数初始化
c1 = 1.49445;
c2 = 1.49445;

maxgen = 50;   % 进化次数  
sizepop = 10;   %种群规模

Vmax = 0.5;   %速度的范围，超过则用边界值。
Vmin = -0.5;  
popmax = 2;   %个体的变化范围
popmin = 1;

%% IV. 产生初始粒子和速度
for i = 1:sizepop
    % 随机产生一个种群
    pop(i,:) = (rands(1) + 1) / 2 + 1;    %初始种群，rands产生(-1,1)，调整到(1,2)
    V(i,:) = 0.5 * rands(1);  %初始化速度
    % 计算适应度
    fitness(i) = fun(pop(i,:));   
end

%% V. 个体极值和群体极值
[bestfitness bestindex] = max(fitness);
zbest = pop(bestindex,:);   %全局最佳
gbest = pop;    %个体最佳
fitnessgbest = fitness;   %个体最佳适应度值
fitnesszbest = bestfitness;   %全局最佳适应度值

%% VI. 迭代寻优
for i = 1:maxgen
    
    for j = 1:sizepop
        % 速度更新
        V(j,:) = V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:));
        V(j,find(V(j,:)>Vmax)) = Vmax;
        V(j,find(V(j,:)popmax)) = popmax;
        pop(j,find(pop(j,:) fitnessgbest(j)
            gbest(j,:) = pop(j,:);
            fitnessgbest(j) = fitness(j);
        end
        
        % 群体最优更新
        if fitness(j) > fitnesszbest
            zbest = pop(j,:);
            fitnesszbest = fitness(j);
        end
    end 
    yy(i) = fitnesszbest;          
end

%% VII. 输出结果并绘图
[fitnesszbest zbest]
plot(zbest, fitnesszbest,'r*')

figure
plot(yy)
title('最优个体适应度','fontsize',12);
xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);