基于Cortex-M3的硬件加速模块
要求:
1、基于m3搭建一个soc,具备ahb、apb两条总线、具备32KB sram 存储器
2、基于apb总线接口设计一个计算模块,该计算模块可以用于加速某种计算,比如sin/cos/pi等,全部由硬件来计算,与软件计算用时进行比较
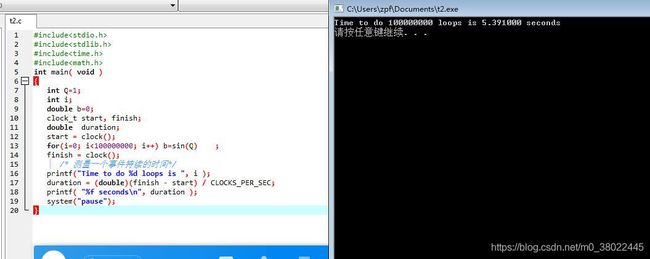
软件计算用时:
t=5.391s/100000000=53.91ns
#include “stdio.h”
#include “stdlib.h”
#include “time.h”
int main( void )
{
int Q=1;
int i;
double b=0;
clock_t start, finish;
double duration;
/* 测量一个事件持续的时间*/
printf( "Time to do %ld loops is ", i );
start = clock();
for (i=0;i<100000000;i++) b=sin(Q) ;
finish = clock();
duration = (double)(finish - start) / CLOCKS_PER_SEC;
printf( "%f seconds\n", duration );
system("pause");
}
SOC设计:包含M3内核/AHB/APB/32K的SRAM(接AHB)/加速模块Accelerate(接APB)
加速模块Accelerate(接APB):
本模块主要针对三角函数的加速计算,计算机出来之前主要通过查表法来进行三角函数求值,即通过已知值重复应用半角和差公式生成;同时还可以用泰勒级数/切比雪夫/最佳一致等概率学方法来实现三角函数值的逼近,这些方法都是通过多项式函数进行近似求值,这种求解方法会涉及到大量浮点运算,对于缺乏硬件乘法器的设备,通过这些方法计算三角函数就非常费时。1959年为解决这种问题,提出了CORDIC(Coordinated Rotation DIgital Computer)算法并在1974年进一步改进,此算法利用移位和加减运算进行三角函数求值,由于只用移位和加法,采用纯硬件方式可以实现。下面对CORDIC算法的原理进行阐述。
CORDIC原理:
CORDIC有两种工作模式,包括旋转/向量模式,在圆/线性/双曲线中可以进行8种不同的运算,具体对应如下:
具体的Cordic算法的原理推导可以参考这篇博客
https://blog.csdn.net/Pieces_thinking/article/details/83512820?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522159419919019195188447152%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=159419919019195188447152&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~first_rank_v2~rank_blog_default-5-83512820.pc_v2_rank_blog_default&utm_term=cordic
我觉得它讲的很详细了。因为本文主要是求解正余弦值,所以只对圆坐标系下的旋转模式部分进行分析:
事实上这个算法可以看作是从0°角向目标角度不断旋转逼近的过程,旋转方向可顺可逆(di=+1/-1),每次的旋转值为设定的
在每次旋转的过程中,旋转的角度是正确的,但是模长变为原来的1/cosb倍,因此再最后要对整个旋转过程中的模长变化进行补偿,引入校模因子,当旋转(迭代)次数趋向于16次时,cosb趋于1,角度已经基本符合所求角度,此时校模因子的多次旋转累积值近似1/An≈0.6072529351。求解过程如下:
取X0=1/An,Y0=0,Z0=求的角度值,迭代计算后即可求得正余弦值。
下面进行Cordic算法的硬件模块实现,
上图为APB接口的Cordic模块。其中使用了apb_slave的PORT3,端口地址为0x4000_3000-0x4000_3FFF,使能寄存器地址0x00,输入相位寄存器地址0x04,输出的sin/cos寄存器地址存放在0x08/0x0c。
软件(Matlab)Cordic算法:(https://blog.csdn.net/qq_39210023/article/details/77456031?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-7.nonecase&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-7.nonecase)
close all;
clear;
clc;
% 初始化
K = 16;%迭代次数
x = zeros(K+1,1);
y = zeros(K+1,1);
z = zeros(K+1,1);
x(1) = 0.607253;%初始设置
z(1) = pi/4;%待求角度θ
%迭代操作
for i = 1:K
if z(i) >= 0
d = 1;
else
d = -1;
end
x(i+1) = x(i) - d*y(i)*(2^(-(i-1)));
y(i+1) = y(i) + d*x(i)*(2^(-(i-1)));
z(i+1) = z(i) - d*atan(2^(-(i-1)));
end
cosa = vpa(x(17),10)
sina = vpa(y(17),10)
c = vpa(z(17),10)硬件Cordic算法:
module Cordic_Test
(
CLK_50M,RST_N,
Phase,
Sin,Cos,Error
);
input CLK_50M;
input RST_N;
input [31:0] Phase;
output [31:0] Sin;
output [31:0] Cos;
output [31:0] Error;
`define rot0 32'd2949120 //45度*2^16
`define rot1 32'd1740992 //26.5651度*2^16
`define rot2 32'd919872 //14.0362度*2^16
`define rot3 32'd466944 //7.1250度*2^16
`define rot4 32'd234368 //3.5763度*2^16
`define rot5 32'd117312 //1.7899度*2^16
`define rot6 32'd58688 //0.8952度*2^16
`define rot7 32'd29312 //0.4476度*2^16
`define rot8 32'd14656 //0.2238度*2^16
`define rot9 32'd7360 //0.1119度*2^16
`define rot10 32'd3648 //0.0560度*2^16
`define rot11 32'd1856 //0.0280度*2^16
`define rot12 32'd896 //0.0140度*2^16
`define rot13 32'd448 //0.0070度*2^16
`define rot14 32'd256 //0.0035度*2^16
`define rot15 32'd128 //0.0018度*2^16
parameter Pipeline = 16;
parameter K = 32'h09b74; //K=0.607253*2^16,32'h09b74,
reg signed [31:0] Sin;
reg signed [31:0] Cos;
reg signed [31:0] Error;
reg signed [31:0] x0=0,y0=0,z0=0;
reg signed [31:0] x1=0,y1=0,z1=0;
reg signed [31:0] x2=0,y2=0,z2=0;
reg signed [31:0] x3=0,y3=0,z3=0;
reg signed [31:0] x4=0,y4=0,z4=0;
reg signed [31:0] x5=0,y5=0,z5=0;
reg signed [31:0] x6=0,y6=0,z6=0;
reg signed [31:0] x7=0,y7=0,z7=0;
reg signed [31:0] x8=0,y8=0,z8=0;
reg signed [31:0] x9=0,y9=0,z9=0;
reg signed [31:0] x10=0,y10=0,z10=0;
reg signed [31:0] x11=0,y11=0,z11=0;
reg signed [31:0] x12=0,y12=0,z12=0;
reg signed [31:0] x13=0,y13=0,z13=0;
reg signed [31:0] x14=0,y14=0,z14=0;
reg signed [31:0] x15=0,y15=0,z15=0;
reg signed [31:0] x16=0,y16=0,z16=0;
reg [ 1:0] Quadrant [Pipeline:0];
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x0 <= 1'b0;
y0 <= 1'b0;
z0 <= 1'b0;
end
else
begin
x0 <= K;
y0 <= 32'd0;
z0 <= Phase[15:0] << 16;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x1 <= 1'b0;
y1 <= 1'b0;
z1 <= 1'b0;
end
else if(z0[31])
begin
x1 <= x0 + y0;
y1 <= y0 - x0;
z1 <= z0 + `rot0;
end
else
begin
x1 <= x0 - y0;
y1 <= y0 + x0;
z1 <= z0 - `rot0;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x2 <= 1'b0;
y2 <= 1'b0;
z2 <= 1'b0;
end
else if(z1[31])
begin
x2 <= x1 + (y1 >>> 1);
y2 <= y1 - (x1 >>> 1);
z2 <= z1 + `rot1;
end
else
begin
x2 <= x1 - (y1 >>> 1);
y2 <= y1 + (x1 >>> 1);
z2 <= z1 - `rot1;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x3 <= 1'b0;
y3 <= 1'b0;
z3 <= 1'b0;
end
else if(z2[31])
begin
x3 <= x2 + (y2 >>> 2);
y3 <= y2 - (x2 >>> 2);
z3 <= z2 + `rot2;
end
else
begin
x3 <= x2 - (y2 >>> 2);
y3 <= y2 + (x2 >>> 2);
z3 <= z2 - `rot2;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x4 <= 1'b0;
y4 <= 1'b0;
z4 <= 1'b0;
end
else if(z3[31])
begin
x4 <= x3 + (y3 >>> 3);
y4 <= y3 - (x3 >>> 3);
z4 <= z3 + `rot3;
end
else
begin
x4 <= x3 - (y3 >>> 3);
y4 <= y3 + (x3 >>> 3);
z4 <= z3 - `rot3;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x5 <= 1'b0;
y5 <= 1'b0;
z5 <= 1'b0;
end
else if(z4[31])
begin
x5 <= x4 + (y4 >>> 4);
y5 <= y4 - (x4 >>> 4);
z5 <= z4 + `rot4;
end
else
begin
x5 <= x4 - (y4 >>> 4);
y5 <= y4 + (x4 >>> 4);
z5 <= z4 - `rot4;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x6 <= 1'b0;
y6 <= 1'b0;
z6 <= 1'b0;
end
else if(z5[31])
begin
x6 <= x5 + (y5 >>> 5);
y6 <= y5 - (x5 >>> 5);
z6 <= z5 + `rot5;
end
else
begin
x6 <= x5 - (y5 >>> 5);
y6 <= y5 + (x5 >>> 5);
z6 <= z5 - `rot5;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x7 <= 1'b0;
y7 <= 1'b0;
z7 <= 1'b0;
end
else if(z6[31])
begin
x7 <= x6 + (y6 >>> 6);
y7 <= y6 - (x6 >>> 6);
z7 <= z6 + `rot6;
end
else
begin
x7 <= x6 - (y6 >>> 6);
y7 <= y6 + (x6 >>> 6);
z7 <= z6 - `rot6;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x8 <= 1'b0;
y8 <= 1'b0;
z8 <= 1'b0;
end
else if(z7[31])
begin
x8 <= x7 + (y7 >>> 7);
y8 <= y7 - (x7 >>> 7);
z8 <= z7 + `rot7;
end
else
begin
x8 <= x7 - (y7 >>> 7);
y8 <= y7 + (x7 >>> 7);
z8 <= z7 - `rot7;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x9 <= 1'b0;
y9 <= 1'b0;
z9 <= 1'b0;
end
else if(z8[31])
begin
x9 <= x8 + (y8 >>> 8);
y9 <= y8 - (x8 >>> 8);
z9 <= z8 + `rot8;
end
else
begin
x9 <= x8 - (y8 >>> 8);
y9 <= y8 + (x8 >>> 8);
z9 <= z8 - `rot8;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x10 <= 1'b0;
y10 <= 1'b0;
z10 <= 1'b0;
end
else if(z9[31])
begin
x10 <= x9 + (y9 >>> 9);
y10 <= y9 - (x9 >>> 9);
z10 <= z9 + `rot9;
end
else
begin
x10 <= x9 - (y9 >>> 9);
y10 <= y9 + (x9 >>> 9);
z10 <= z9 - `rot9;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x11 <= 1'b0;
y11 <= 1'b0;
z11 <= 1'b0;
end
else if(z10[31])
begin
x11 <= x10 + (y10 >>> 10);
y11 <= y10 - (x10 >>> 10);
z11 <= z10 + `rot10;
end
else
begin
x11 <= x10 - (y10 >>> 10);
y11 <= y10 + (x10 >>> 10);
z11 <= z10 - `rot10;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x12 <= 1'b0;
y12 <= 1'b0;
z12 <= 1'b0;
end
else if(z11[31])
begin
x12 <= x11 + (y11 >>> 11);
y12 <= y11 - (x11 >>> 11);
z12 <= z11 + `rot11;
end
else
begin
x12 <= x11 - (y11 >>> 11);
y12 <= y11 + (x11 >>> 11);
z12 <= z11 - `rot11;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x13 <= 1'b0;
y13 <= 1'b0;
z13 <= 1'b0;
end
else if(z12[31])
begin
x13 <= x12 + (y12 >>> 12);
y13 <= y12 - (x12 >>> 12);
z13 <= z12 + `rot12;
end
else
begin
x13 <= x12 - (y12 >>> 12);
y13 <= y12 + (x12 >>> 12);
z13 <= z12 - `rot12;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x14 <= 1'b0;
y14 <= 1'b0;
z14 <= 1'b0;
end
else if(z13[31])
begin
x14 <= x13 + (y13 >>> 13);
y14 <= y13 - (x13 >>> 13);
z14 <= z13 + `rot13;
end
else
begin
x14 <= x13 - (y13 >>> 13);
y14 <= y13 + (x13 >>> 13);
z14 <= z13 - `rot13;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x15 <= 1'b0;
y15 <= 1'b0;
z15 <= 1'b0;
end
else if(z14[31])
begin
x15 <= x14 + (y14 >>> 14);
y15 <= y14 - (x14 >>> 14);
z15 <= z14 + `rot14;
end
else
begin
x15 <= x14 - (y14 >>> 14);
y15 <= y14 + (x14 >>> 14);
z15 <= z14 - `rot14;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x16 <= 1'b0;
y16 <= 1'b0;
z16 <= 1'b0;
end
else if(z15[31])
begin
x16 <= x15 + (y15 >>> 15);
y16 <= y15 - (x15 >>> 15);
z16 <= z15 + `rot15;
end
else
begin
x16 <= x15 - (y15 >>> 15);
y16 <= y15 + (x15 >>> 15);
z16 <= z15 - `rot15;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
Quadrant[0] <= 1'b0;
Quadrant[1] <= 1'b0;
Quadrant[2] <= 1'b0;
Quadrant[3] <= 1'b0;
Quadrant[4] <= 1'b0;
Quadrant[5] <= 1'b0;
Quadrant[6] <= 1'b0;
Quadrant[7] <= 1'b0;
Quadrant[8] <= 1'b0;
Quadrant[9] <= 1'b0;
Quadrant[10] <= 1'b0;
Quadrant[11] <= 1'b0;
Quadrant[12] <= 1'b0;
Quadrant[13] <= 1'b0;
Quadrant[14] <= 1'b0;
Quadrant[15] <= 1'b0;
Quadrant[16] <= 1'b0;
end
else
begin
Quadrant[0] <= Phase[17:16];
Quadrant[1] <= Quadrant[0];
Quadrant[2] <= Quadrant[1];
Quadrant[3] <= Quadrant[2];
Quadrant[4] <= Quadrant[3];
Quadrant[5] <= Quadrant[4];
Quadrant[6] <= Quadrant[5];
Quadrant[7] <= Quadrant[6];
Quadrant[8] <= Quadrant[7];
Quadrant[9] <= Quadrant[8];
Quadrant[10] <= Quadrant[9];
Quadrant[11] <= Quadrant[10];
Quadrant[12] <= Quadrant[11];
Quadrant[13] <= Quadrant[12];
Quadrant[14] <= Quadrant[13];
Quadrant[15] <= Quadrant[14];
Quadrant[16] <= Quadrant[15];
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
Cos <= 1'b0;
Sin <= 1'b0;
Error <= 1'b0;
end
else
begin
Error <= z16;
case(Quadrant[16])
2'b00: //if the Phase is in first Quadrant,the Sin(X)=Sin(A),Cos(X)=Cos(A)
begin
Cos <= x16;
Sin <= y16;
end
2'b01: //if the Phase is in second Quadrant,the Sin(X)=Sin(A+90)=CosA,Cos(X)=Cos(A+90)=-SinA
begin
Cos <= ~(y16) + 1'b1;//-Sin
Sin <= x16;//Cos
end
2'b10: //if the Phase is in third Quadrant,the Sin(X)=Sin(A+180)=-SinA,Cos(X)=Cos(A+180)=-CosA
begin
Cos <= ~(x16) + 1'b1;//-Cos
Sin <= ~(y16) + 1'b1;//-Sin
end
2'b11: //if the Phase is in forth Quadrant,the Sin(X)=Sin(A+270)=-CosA,Cos(X)=Cos(A+270)=SinA
begin
Cos <= y16;//Sin
Sin <= ~(x16) + 1'b1;//-Cos
end
endcase
end
end
endmodule
cordic模块的APB接口:
// -----------------------------------------------------------------------------
// Copyright (c) 2014-2020 All rights reserved
// -----------------------------------------------------------------------------
// Author : zhou_hua
// File : apb_accelerate.v
// Create : 2020-07-08 08:48:36
// Revise : 2020-07-08 08:48:36
// Editor : sublime text3, tab size (4)
// Function: Cordic algorithm to calculate sin/cos
// Address : 0x4000_1000-0x4000_1FFF PADDR[11:2]
// 0x00 RW ENABLE
// 0X04 RW PHASE_IN
// 0X08 R SIN
// 0X0C R COS
// -----------------------------------------------------------------------------
module apb_accelerate(
input PCLK,
//input PCLKG,//Gate clock(reduce power)
input PRESETn,
input PENABLE,
input PSEL,
input [11:2] PADDR,
input PWRITE,
input [31:0] PWDATA,
input signed [31:0] Sin,
input signed [31:0] Cos,
output wire [31:0] PRDATA,
output reg [31:0] Phase,
output PREADY, // Device ready
output PSLVERR// Device error response
);
// Signals for Control registers
reg [3:0] reg_ctrl;
// Signals for read/write controls
wire read_enable;
wire write_enable;
wire write_enable00; // Write enable for Control register
wire write_enable04; // Write enable for Phase Value register
wire write_enable08; // Read enable for sin Value register
wire write_enable0c; // Read enable for cos Value register
// Read and write control signals
assign read_enable = PSEL & (~PWRITE); // assert for whole APB read transfer
assign write_enable = PSEL & (~PENABLE) & PWRITE; // assert for 1st cycle of write transfer
assign write_enable00 = write_enable & (PADDR[11:2] == 10'h000);//Write enable for ENABLE register
assign write_enable04 = write_enable & (PADDR[11:2] == 10'h001);//Write enable for PHASE_IN register
assign read_enable08 = read_enable & (PADDR[11:2] == 10'h002);//Write enable for SIN register
assign read_enable0c = read_enable & (PADDR[11:2] == 10'h003);//Write enable for COS register
//write operatiom
//ENABLE reg
always @(posedge PCLK or negedge PRESETn)
begin
if (~PRESETn)
reg_ctrl <= {4{1'b0}};
else if (write_enable00)
reg_ctrl <= PWDATA[3:0];
end
// Phase IN Value register
always @(posedge PCLK or negedge PRESETn)
begin
if (~PRESETn)
Phase <= {32{1'b0}};
else if (write_enable04)
Phase <= PWDATA[31:0];
end
// Read operation
// Output read data to APB
assign PRDATA = (read_enable08) ? Sin : {32{1'b0}};
assign PRDATA = (read_enable0c) ? Cos : {32{1'b0}};
assign PREADY = 1'b1; // Always ready
assign PSLVERR = 1'b0; // Always okay
//Cordic part
endmodule
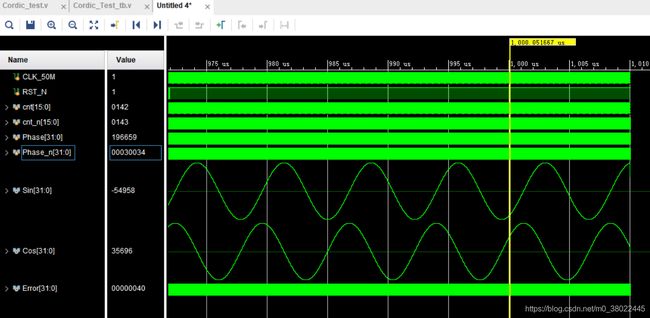
正余弦测试波形:
APB模块:(apb_slave_mux+apb_subsystem(top)+ahb_to_apb)
apb_slave_mux:内部比较简单,包括四位的选择器和简单的组合逻辑从而对PSELx赋值对16个外设模块进行选中,以及PREADY/PSLVERR控制信号的赋值
ahb_to_apb:进行AHB总线到APB总线的桥接,APB控制和读写到AHB的转换,以及APB读写时序的状态机(准备-等待传输-APB第一次传输-APB第二次传输-传输完成发出OKAY-错误返回的第一周期-错误返回第二周期-非法状态)
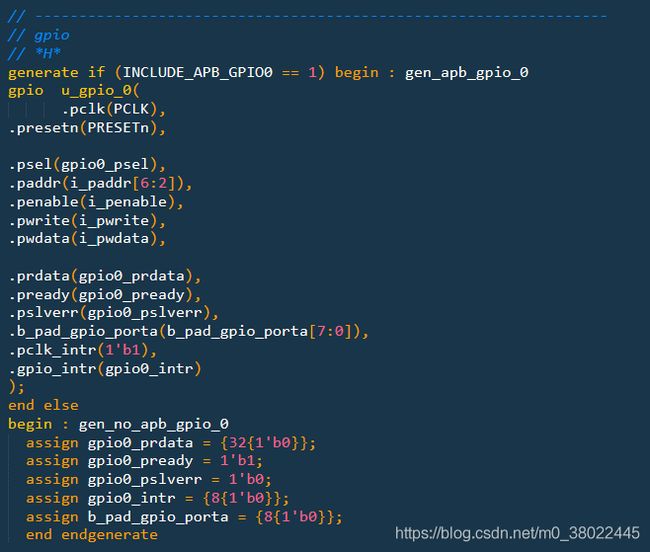
apb_subsystem:定义各个外设模块的apb接口,内部例化了一个apb_slave_mux和ahb_to_apb桥接器,然后对外设模块进行例化,在对外设实例化的过程中使用条件生成语句。生成语句可以动态地生成Verilog代码,当对矢量中的多个位进行重复操作时,或者当进行多个模块的实例引用的重复操作时,或条件判断是否需要当前的Verilog代码时,使用生成语句能大大简化程序编写过程。以我们做的gpio模块为例:
当外部参数GPIO==1时进行实例化,不用的时候就使用简单的组合逻辑给GPIO的接口赋0,可以降低功耗(maybe)。语法一般如下:
generate
if ()
//对A进行实例化
else
//对B进行实例化
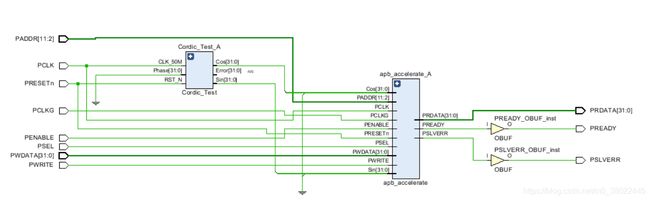
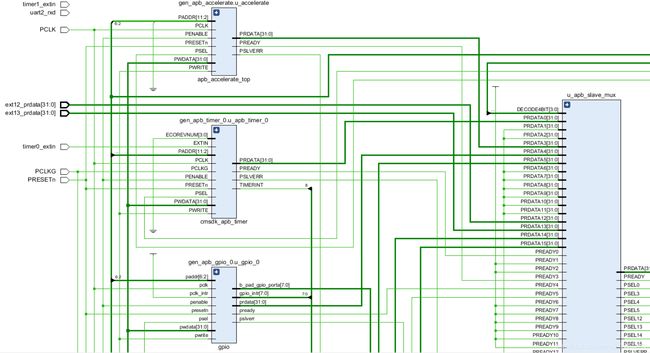
endgenerate对上述模块进行设计后综合出来的电路如下所示,观察信号线基本没有问题:
APB模块测试完毕后将其通过AHB2APB桥接器连接至AHB总线,进行SOC的软硬件协同仿真。
Keil测试代码如下:
//测试
addr = (int*)0x9000;
*addr = 0x11223344;
//Accelerate使能
TADDR =(int*)0x40003000;
*TADDR = 0x00000001;
//Accelerate加载相位值
TADDR =(int*)0x40003004;
*TADDR =0x2d; //45°
//sin读
TADDR =(int*)0x40003008;
//cos读
TADDR =(int*)0x4000300C;
//Accelerate加载相位值
TADDR =(int*)0x40003004;
*TADDR =0x1e; //30°
//sin读
TADDR =(int*)0x40003008;
//cos读
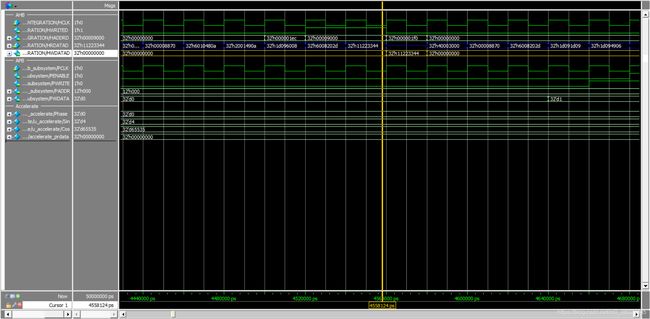
TADDR =(int*)0x4000300C;首先进行SOC数据传输测试,向0x9000传输测试数据,波形如下:
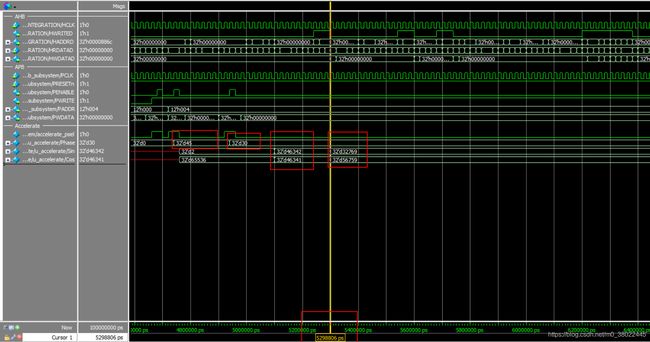
SOC测试完毕,对加速模块进行测试,首先对模块给使能,之后输入相位45°-30°,观察输出结果: