Matlab数字图像处理——图像增强

一、图像增强介绍

• 图像增强的目的：提高图像质量和可辨识度
• 图像质量的评价：图像的逼真度和可懂度

二、灰度变换增强

1、获取图像灰度直方图

灰度变换增强：改变图像像素灰度值

可通过Matlab函数 imhist 获取图像灰度直方图

I = imread('火影4.jpg');
I = rgb2gray(I);

row = size(I, 1);
column = size(I, 2);
N = zeros(1, 256);

for i = 1:row
    for j = 1:column
        k = I(i, j);
        N(k + 1) = N(k + 1) + 1;
    end
end

figure;
subplot(121);imshow(I);
subplot(122);bar(N);

结果展示：

2、通过调整灰度值来增强图像

I = imread('火影4.jpg');
I = rgb2gray(I);
I = double(I);

J = (I - 80) * 255 / 70;
row = size(I, 1);
column = size(I, 2);

for i = 1:row
    for j = 1:column
        if J(i, j) < 0
            J(i, j) = 0;
        elseif J(i, j) > 255
            J(i, j) = 255;
        end
    end
end

figure;
subplot(121);imshow(uint8(I));
subplot(122);imshow(uint8(J));

结果展示：

从结果看，来回调整灰度值，感觉跟美颜相机调整亮度差不多？

三、直方图增强

直方图反映了图像灰度值的分布情况，直方图增强的原理就是通过影响灰度值的分布情况来增强图像。

常用的直方图调整方法包括直方图均衡化、直方图规定化

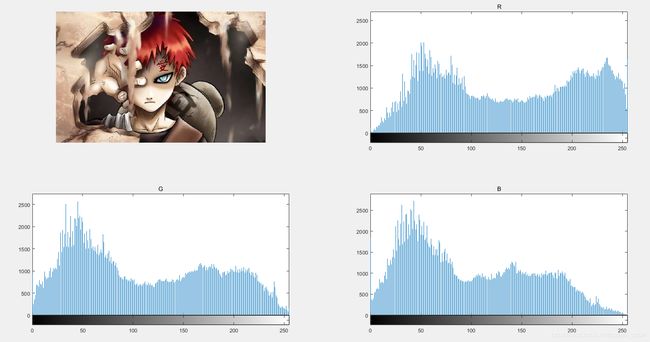
1、彩色RGB图像直方图显示

I = imread('火影6.jpg');

figure;
subplot(221);imshow(I);
subplot(222);imhist(I(:, :, 1));title('R');
subplot(223);imhist(I(:, :, 2));title('G');
subplot(224);imhist(I(:, :, 3));title('B');

结果展示：

2、直方图均衡化

Matlab直方图均衡化函数：histeq

I = imread('火影1.jpg');
J = histeq(I);

figure;
subplot(221);imshow(I);
subplot(222);imshow(J);
subplot(223);imhist(I);
subplot(224);imhist(J);

结果展示：

从结果可以看出灰度值分布明显的更平均了，实际图像看上去色彩对比没有那么强烈了

3、直方图近似化

Matlab提供的函数 histeq 还可以让直方图分布情况近似于给定的分布情况，例如下列代码，让图像的直方图分布去近似正态分布：

I = imread('火影1.jpg');
G = randn(1, 256);
J = histeq(I, G);

figure;
subplot(231);imshow(I);title('原图');
subplot(232);imshow(J);title('近似后');
subplot(233);imhist(I);title('原图像直方图分布情况');
subplot(234);imhist(J);title('近似后分布情况');
subplot(235);bar(G);title('近似的参考分布');

结果展示：

四、图像的统计特性

• 1、图像的标准差函数：std2
• 2、图像的平均数函数：mean2
• 3、绘制图像等高线函数：imcontour

I = imread('火影4.jpg');
I = rgb2gray(I);

figure;
subplot(121);imshow(I);
subplot(122);imcontour(I);

五、空域滤波

空域滤波的原理：

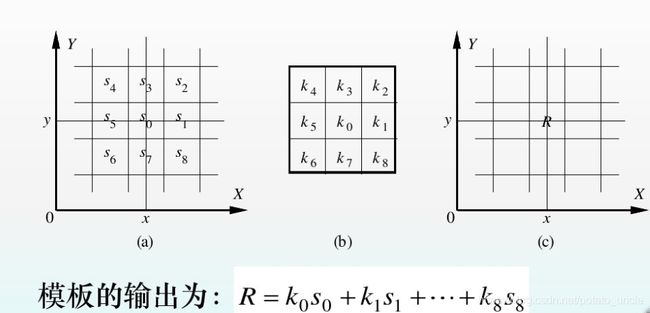
1、图 a 为要进行滤波的原图像，图 b 为滤波模板，图 c 为滤波后的结果
2、首先选定像素点 s₀ ，使用模板使原图像 s₀ 及其周围的点与模板设定好的系数对应相乘，其结果相加得到R， 使R替换 s₀，则完成滤波操作

这一部分的图像就用我超级喜欢的自来也吧！！这张是原图：

1、线性平均滤波

Matlab提供滤波函数：imfilter

I = imread('火影7.jpg');
I = rgb2gray(I);    %读入灰度图像

J = imnoise(I, 'salt & pepper', 0.02);    %加入椒盐噪声
h = ones(3, 3) / 5;  %设置滤波模板
h(1, 1) = 0;
h(1, 3) = 0;
h(3, 1) = 0;
h(1, 3) = 0;

K = imfilter(J, h);    %进行空域滤波

figure;
subplot(131);imshow(I);title('原灰度图');
subplot(132);imshow(J);title('加椒盐噪声');
subplot(133);imshow(K);title('空域滤波');

结果展示：

图三对比图二可以明显的看出椒盐噪声没那么明显了

2、卷积

Matlab卷积操作函数：conv2
下列代码为卷积操作：

I = imread('火影7.jpg');
I = rgb2gray(I);    %读入灰度图像
I = im2double(I);

J = imnoise(I, 'gaussian', 0, 0.01);    %加入高斯噪声
h = ones(3, 3) / 9;  %设置滤波模板

K = conv2(J, h);    %进行卷积操作

figure;
subplot(131);imshow(I);title('原灰度图');
subplot(132);imshow(J);title('加高斯噪声');
subplot(133);imshow(K);title('卷积');

图三对比图二也可以明显的看出高斯噪声没那么明显了

3、二维中值滤波

Matlab提供中值滤波的函数：medfilt2

二维中值滤波可以有效的去除椒盐噪声，效果比均值滤波要好

I = imread('火影7.jpg');
I = rgb2gray(I);    %读入灰度图像
I = im2double(I);

J = imnoise(I, 'salt & pepper', 0.03);    %加入椒盐噪声

K = medfilt2(J);    %进行二维中值滤波

figure;
subplot(131);imshow(I);title('原灰度图');
subplot(132);imshow(J);title('加椒盐噪声');
subplot(133);imshow(K);title('中值滤波');

完全看不出椒盐噪声！！ 真 TMD 好！！

4、顺序统计滤波

Matlab提供顺序统计滤波函数：ordfilt2

I = imread('火影7.jpg');
I = rgb2gray(I);    %读入灰度图像
I = im2double(I);

K1 = ordfilt2(I, 1, true(5));    %相当于最小值滤波
K2 = ordfilt2(I, 25, true(5));   %最大值滤波

figure;
subplot(131);imshow(I);title('原灰度图');
subplot(132);imshow(K1);
subplot(133);imshow(K2);

采用5 x 5模板最小值输出会使图像更暗，5 x 5最大值输出使图像更亮，同时这两种输出都使图像更模糊了。。。

5、自适应滤波

Matlab自适应滤波函数：wiener2

I = imread('火影7.jpg');
I = rgb2gray(I);    %读入灰度图像
I = im2double(I);

J = imnoise(I, 'gaussian', 0, 0.01);    %加入高斯噪声

K = wiener2(J, [5, 5]);    %进行卷积操作

figure;
subplot(131);imshow(I);title('原灰度图');
subplot(132);imshow(J);title('加高斯噪声');
subplot(133);imshow(K);title('自适应滤波');

六、频域滤波

1、低通滤波

低通滤波器原理是让低频通过，衰减或过滤掉高频滤波，从而过滤掉包含在高频中的噪声。其作用是图像的去噪声平滑增强，但也会造成不同程度的模糊

(1)、理想低通滤波器

$$D(u,v)=[(u-M/2{)}^2+(v-N/2{)}^2{]}^{1/2}$$
其中 D(u, v) 表示频率域中点 (u, v) 与频率矩形中心的距离，该距离若大于预先设定距离D₀则该点值为0，小于或等于则保留原值。

I = imread('火影8.jpg');
I = rgb2gray(I);    %读入灰度图像
I = im2double(I);

M = 2 * size(I, 1);
N = 2 * size(I, 2);

u = -M / 2:(M / 2 - 1);
v = -N / 2:(N / 2 - 1);
[U, V] = meshgrid(u, v);           %基于向量 u 和 v 中包含的坐标返回二维网格坐标
D = sqrt(U.^2 + V.^2);
D0 = 80;                           %滤波器截止频率为80
H = double(D<= D0);
J = fftshift(fft2(I, size(H, 1), size(H, 2)));  %fftshift将零频点移到频谱的中间,fft2二维快速傅里叶变换
K = J.*H;
L = ifft2(ifftshift(K));           %二维快速傅里叶逆变换
L = L(1: size(I, 1), 1: size(I, 2));
figure;
subplot(121);imshow(I);
subplot(122);imshow(L);

结果表明，效果真的不咋地：

(2)、Butterworth低通滤波器

截止频率位于距原点 D₀ 处的 n 阶Butterworth低通滤波器(BLPF)的传递函数定义为：
$$H(u,v)=\frac{1}{1+[D(u,v)/D_0{]}^{2n}}$$

I = imread('火影8.jpg');
I = rgb2gray(I);    %读入灰度图像
I = im2double(I);

M = 2 * size(I, 1);
N = 2 * size(I, 2);

u = -M / 2:(M / 2 - 1);
v = -N / 2:(N / 2 - 1);
[U, V] = meshgrid(u, v);           %基于向量 u 和 v 中包含的坐标返回二维网格坐标
D = sqrt(U.^2 + V.^2);
D0 = 80;                           %滤波器截止频率为80
n = 6;
H = 1./ (1 + (D./ D0).^ (2 * n));
J = fftshift(fft2(I, size(H, 1), size(H, 2)));  %fftshift将零频点移到频谱的中间,fft2二维快速傅里叶变换
K = J.*H;
L = ifft2(ifftshift(K));           %二维快速傅里叶逆变换
L = L(1: size(I, 1), 1: size(I, 2));
figure;
subplot(121);imshow(I);
subplot(122);imshow(L);

结果也是很糊：

2、高通滤波

高通滤波器原理是让高频通过，衰减或过滤掉低频滤波。其作用是使图像得到锐化处理，突出图像边界

(1)、Butterworth高通滤波器

截止频率位于距原点 D₀ 处的 n 阶Butterworth高通滤波器(BHPF)的传递函数定义为：
$$H(u,v)=\frac{1}{1+[D_0/D(u,v){]}^{2n}}$$

I = imread('火影8.jpg');
I = rgb2gray(I);    %读入灰度图像
I = im2double(I);

M = 2 * size(I, 1);
N = 2 * size(I, 2);

u = -M / 2:(M / 2 - 1);
v = -N / 2:(N / 2 - 1);
[U, V] = meshgrid(u, v);           %基于向量 u 和 v 中包含的坐标返回二维网格坐标
D = sqrt(U.^2 + V.^2);
D0 = 30;                           %滤波器截止频率为30
n = 6;
H = 1./ (1 + (D0./ D).^ (2 * n));
J = fftshift(fft2(I, size(H, 1), size(H, 2)));  %fftshift将零频点移到频谱的中间,fft2二维快速傅里叶变换
K = J.*H;
L = ifft2(ifftshift(K));           %二维快速傅里叶逆变换
L = L(1: size(I, 1), 1: size(I, 2));
figure;
subplot(121);imshow(I);
subplot(122);imshow(L);

可以明显地突出图像的边缘部分：

(2)、高斯高通滤波器

截止频率处在距频率矩形中心距离为 D₀ 的高斯高通滤波器(GHPF)的传递函数由下式给出：
$$H(u,v)=1-e^{-D^2(u,v)/2D_0^2}$$
该滤波器结果要更加平滑，即使对微小物体和细线条滤波结果也比较清晰

I = imread('火影8.jpg');
I = rgb2gray(I);    %读入灰度图像
I = im2double(I);

M = 2 * size(I, 1);
N = 2 * size(I, 2);

u = -M / 2:(M / 2 - 1);
v = -N / 2:(N / 2 - 1);
[U, V] = meshgrid(u, v);           %基于向量 u 和 v 中包含的坐标返回二维网格坐标
D = sqrt(U.^2 + V.^2);
D0 = 20;                           %滤波器截止频率为20
H = 1 - exp(-(D.^2)./(2 * (D0^2)));
J = fftshift(fft2(I, size(H, 1), size(H, 2)));  %fftshift将零频点移到频谱的中间,fft2二维快速傅里叶变换
K = J.*H;
L = ifft2(ifftshift(K));           %二维快速傅里叶逆变换
L = L(1: size(I, 1), 1: size(I, 2));
figure;
subplot(121);imshow(I);
subplot(122);imshow(L);

结果展示：

3、理想带阻滤波器

带阻滤波器用于抑制距离频率域中心一定距离的一个圆环区域的频率，可用于消除一定频率范围的周期噪声。

I = imread('火影8.jpg');
I = rgb2gray(I);    %读入灰度图像
I = imnoise(I, 'gaussian', 0, 0.01);    %加入高斯噪声
I = im2double(I);

M = 2 * size(I, 1);
N = 2 * size(I, 2);

u = -M / 2:(M / 2 - 1);
v = -N / 2:(N / 2 - 1);
[U, V] = meshgrid(u, v);           %基于向量 u 和 v 中包含的坐标返回二维网格坐标
D = sqrt(U.^2 + V.^2);
D0 = 50;                           %滤波器截止频率为50
W = 30;
H = double(or(D < (D0 - W / 2), D > D0 + W / 2));

J = fftshift(fft2(I, size(H, 1), size(H, 2)));  %fftshift将零频点移到频谱的中间,fft2二维快速傅里叶变换
K = J.*H;
L = ifft2(ifftshift(K));           %二维快速傅里叶逆变换
L = L(1: size(I, 1), 1: size(I, 2));
figure;
subplot(121);imshow(I);
subplot(122);imshow(L);

4、同态滤波

同态滤波可以压缩灰度图像的动态范围，且增强对比度

I = imread('pout.tif');
J = log(im2double(I) + 1);
K = fft2(J);
n = 5;
D0 = 0.1 * pi;
rh = 0.7;
rl = 0.4;
[row, column] = size(J);

for i = 1: row
    for j = 1: column
        D1(i, j) = sqrt(i^2 + j^2);
        H(i, j) = rl + (rh / (1 + (D0 / D1(i, j))^(2 * n)));
    end
end

L = K.*H;
M = ifft2(L);
N = exp(M) - 1;

figure;
subplot(121);imshow(I);
subplot(122);imshow(real(N));

完整目录

Matlab数字图像处理——图像处理工具箱Image Processing Toolbox
Matlab数字图像处理——图像类型的转换
Matlab数字图像处理——图像文件的读取
Matlab数字图像处理——图像文件的显示
Matlab数字图像处理——视频文件的读写
Matlab数字图像处理——图像的像素运算(灰度变换)
Matlab数字图像处理——图像的空间变换
Matlab数字图像处理——图像的平移、邻域操作、区域选取
Matlab数字图像处理——图像增强
Matlab数字图像处理——图像复原