PSO粒子群算法调节PID控制器参数

概述

PSO（粒子群算法）在处理连续问题上有着较强的能力，因此很适合用来做参数优化，而PID控制器由三个参数组成，它们分别是：
$$K_p、K_i、K_d$$
我们可以把PID控制器当做一个“黑箱”，输入为这三个参数，输出为响应曲线，我们要做的就是优化这个响应曲线。而一个控制效果好的PID控制器应针对不同类型输入都有较快的响应速度，较小的超调以及稳态误差。因此我们将经典的三种输入信号：阶跃、斜坡、抛物用来衡量PID控制效果。

适应函数设计

我们选用综合指标来衡量设计效果,由于是数字控制器，我们选用求和而不是积分的方式：
$$W=\Sigma e^2(i)$$
又因为我们考虑了三种输入，因此：
$$\Sigma W=\Sigma \Sigma e^2(i)$$
下面是编写的适应函数：

function return_value = PID_find_betterparameters(Kp,Ki,Kd)
    t = 1:50;
    ideal = 5;
    x=[];e=[];
    x(1)=0;
    for i = t                   %阶跃输入
        e(i) = ideal - x(i);
        if(i>1)
            x(i+1) = x(i) + Kp*e(i) + Ki*sum(e) + Kd*(e(i)-e(i-1));
        end
        if i==1
            x(i+1) = x(i) + Kp*e(i) + Ki*sum(e);
        end
    end
    for j = t
        s(j) = (x(j)-ideal)^2;
    end
    return_value1 = sum(s);

    for i = t                      %斜坡输入
        e(i) = ideal*i - x(i);
        if(i>1)
            x(i+1) = x(i) + Kp*e(i) + Ki*sum(e) + Kd*(e(i)-e(i-1));
        end
        if i==1
            x(i+1) = x(i) + Kp*e(i) + Ki*sum(e);
        end
    end
    for j = t
        s(j) = (x(j)-ideal*j)^2;
    end
    return_value2 = sum(s);
    
    for i = t                          %抛物输入
        e(i) = ideal*i^2 - x(i);
        if(i>1)
            x(i+1) = x(i) + Kp*e(i) + Ki*sum(e) + Kd*(e(i)-e(i-1));
        end
        if i==1
            x(i+1) = x(i) + Kp*e(i) + Ki*sum(e);
        end
    end
    for j = t
        s(j) = (x(j)-ideal*j^2)^2;
    end
    return_value3 = sum(s);
    
    return_value = (return_value1 + return_value2 + return_value3)/100;
end

PSO优化

之前也说到，我们将PID控制器当做一个“黑箱”来处理，它的返回值是 $e$ ，输入维数为3，也就是一个三元函数。下面给出粒子群优化代码：

%---------------粒子群优化寻PID参数----------------%
close all;clear;clc;
maxgen = 100;
sizepop = 60;
Vmax = 0.5;
Vmin = -0.5;
popmax = 2;
popmin = -2;
c1 = 0.3;
c2 = 1.5;
%------------------初始化种群-----------------------%
for i = 1:sizepop
    pop(i,:) = -2+4*rand(1,3);
    V(i,:) = rand(1,3);
    fitness(i) = PID_find_betterparameters(pop(i,1),pop(i,2),pop(i,3));
end

[bestfitness,bestindex] = min(fitness);
fitnesszbest = bestfitness;
fitnessgbest = fitness;
zbest = pop(bestindex,:);     %种群历史最优解
gbest = pop;                  %个体历史最优解

%---------------寻优--------------------------%
for i = 1:maxgen
    for j = 1:sizepop
        %-----------速度更新-----------------%
        V(j,:) = V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:));
        V(j,find(V(j,:)>Vmax)) = Vmax;           %限制搜索速度
        V(j,find(V(j,:)<Vmin)) = Vmin;
        
        %----------种群更新------------------%
        pop(j,:) = pop(j,:) + V(j,:);
        pop(j,find(pop(j,:)>popmax)) = popmax;    %限制搜索范围
        pop(j,find(pop(j,:)<popmin)) = popmin;
        
        %----------更新适应值----------------%
        fitness(j) = PID_find_betterparameters(pop(j,1),pop(j,2),pop(j,3));
    end
    %----------------个体最优更新-------------%
    for j = 1:sizepop
        if (fitness(j)<fitnessgbest(j))
            gbest(j,:) = pop(j,:);
            fitnessgbest(j,:) = fitness(j);
        end
        if (fitness(j)<fitnesszbest)
            zbest = pop(j,:);
            fitnesszbest = fitness(j);
        end
    end
    yy(i) = fitnesszbest;  %每一代的最优适应值
    
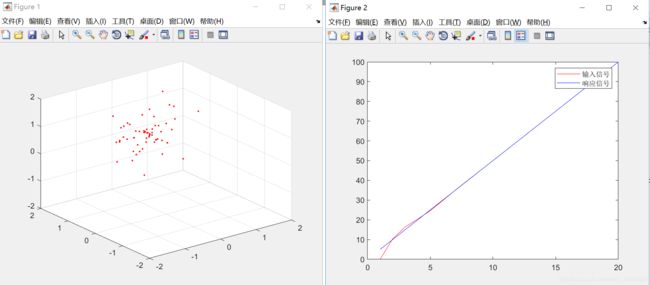
    %---------------绘制搜索动态3D图---------------%
    if (i>1) 
        delete(G); 
    end
    G = scatter3(pop(:,1),pop(:,2),pop(:,3),40,'r.');
    xlim([-2,2]);
    ylim([-2,2]);
    zlim([-2,2]);
    drawnow
    hold on
    pause(0.05);
end

输出最优参数和对应适值：

zbest                          %最优参数
fitnesszbest                   %最优参数对应的适值

绘制响应动态图（以斜坡为例）：

%------------------绘制响应-----------------------------%
t = 1:100;
ideal = 5;
x=[];e=[];
x(1)=0;
Kp = zbest(1); Ki = zbest(2); Kd = zbest(3);
for i = t
    e(i) = ideal*i - x(i);
    if(i>1)
        x(i+1) = x(i) + Kp*e(i) + Ki*sum(e) + Kd*(e(i)-e(i-1));
    end
    if i==1
        x(i+1) = x(i) + Kp*e(i) + Ki*sum(e);
    end
end
figure(2);
plot(1:101,x,'r');
xlim([0,20]);
hold on;
plot(1:101,5*[1:101],'b');
xlim([0,20]);

总结

我们利用PSO处理连续问题的优势对工程上常用的PID控制进行优化，虽然现在大部分的PID参数调节都是依靠经验，但是在不久的将来，智能算法的进步一定会促使控制算法参数调节更为便捷。