window10下安装python3.7.2环境及opencv简单安装测试

1、安装python
下载python3.7.2版本，下载地址：https://www.python.org/downloads/release/python-372/；可以根据需求选择合适的版本下载。

下载后直接点击文件进行安装，选择第二个箭头，可以选择安装在可选目录下，若选择第一个箭头则安装在默认目录下。勾选添加环境，系统自动配置环境，否则到计算机-属性-高级系统设置-环境变量-系统变量Path中加入python的路径

选择将安装的目录

安装成功后在控制台输入python，可以看到如下信息

输入pip list 安装python时自动安装了pip，若无则需到官网下载pip 在控制台输入python setup.py install（同样需添加环境变量）

2、安装opencv
cmd中输入：pip install opencv-python，进行下载，若下载失败则到https://www.lfd.uci.edu/~gohlke/pythonlibs/#opencv寻找下载需要的版本。

3.安装PIL
cmd中输入：pip install pilow，进行安装

4.调试
打开IDLE，进行代码调试

5.图像直方图显示：
导入代码需要的工具包，如无则需要到cmd中进行模块命令语句安装

from PIL import Image
from numpy import *
from pylab import *
import matplotlib.pyplot as PLT

#读取图像到数组并转化成灰度图像
pil_im =array(Image.open('test.jpg').convert('L'))

figure()
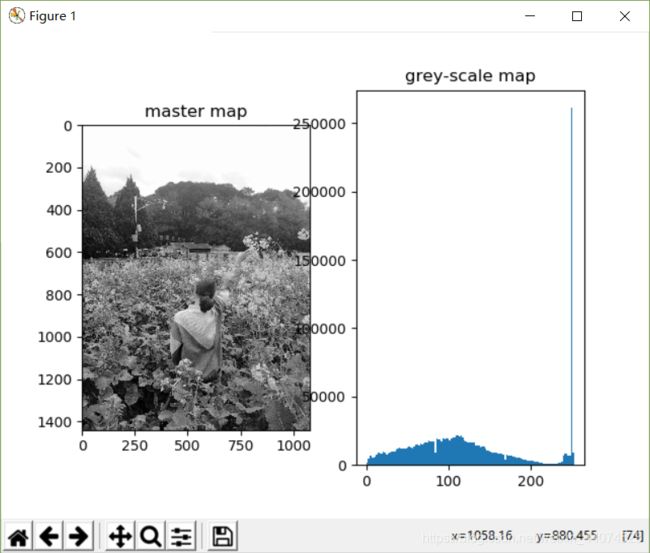
subplot(1,2,1),imshow(pil_im,plt.cm.gray),title('master map')
subplot(1,2,2),hist(pil_im.flatten(),128),title('grey-scale map')
show()

6.直方图均衡化
对图像进行非线性拉伸,重新分配图像象元值,使一定灰度范围内象元值的数量大致相等。

from PIL import Image
from numpy import *
from pylab import *
import matplotlib.pyplot as PLT
def histep(im,nbr_bins=256):
    imhist,bins=histogram(im.flatten(),nbr_bins,normed=True)
    cdf=imhist.cumsum()#积累分布函数
    cdf=255*cdf/cdf[-1]#归一化
    im2=interp(im.flatten(),bins[:-1],cdf)
    return im2.reshape(im.shape),cdf
 
im=array(Image.open('test.jpg').convert('L'))
im2,cdf=histep(im)#


figure()
subplot(2,2,1),imshow(im,plt.cm.gray),title('master map')
subplot(2,2,2),hist(im.flatten(),128),title('master map histogram')
subplot(2,2,3),imshow(im2,plt.cm.gray),title('equilibrium figures')
subplot(2,2,4),hist(im2.flatten(),128),title('equilibrium figures histogram')
show()

7.高斯滤波处理
a.灰度图像高斯滤波处理

from PIL import Image
from numpy import *
from pylab import *
from scipy.ndimage import filters


#读取图像到数组并转化成灰度图像
pil_im =array(Image.open('test.jpg').convert('L'))
gray()
im=filters.gaussian_filter(pil_im,2)
im11=filters.gaussian_filter(pil_im,5)
im111=filters.gaussian_filter(pil_im,10)
figure()
axis('equal')
axis('off')
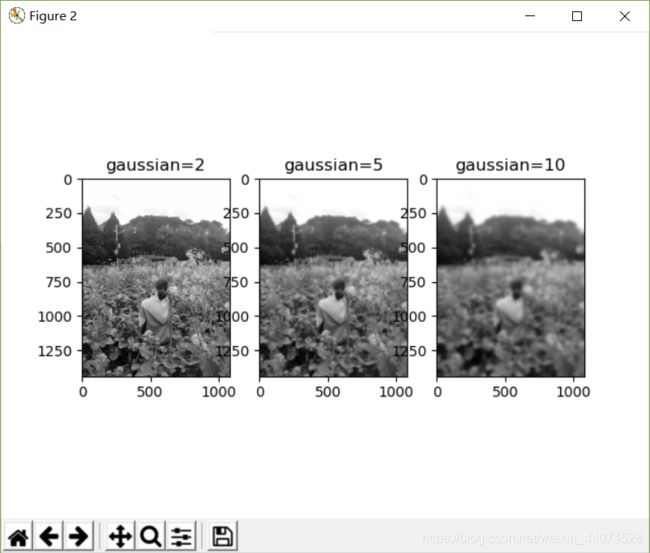
subplot(1,3,1),imshow(im),title('gaussian=2')
subplot(1,3,2),imshow(im11),title('gaussian=5')
subplot(1,3,3),imshow(im111),title('gaussian=10')
show()

b.彩色图像的高斯处理

from PIL import Image
from numpy import *
from pylab import *
from scipy.ndimage import filters

im1 = array(Image.open('test.jpg'))
axis('equal')
axis('off')

im2 = zeros(im1.shape)
for i in range(3):
    im2[:,:,i] = filters.gaussian_filter(im1[:,:,i],2)
im2 = uint8(im2)

im22 = zeros(im1.shape)
for i in range(3):
    im22[:,:,i] = filters.gaussian_filter(im1[:,:,i],5)
im22 = uint8(im22)

im222 = zeros(im1.shape)
for i in range(3):
    im222[:,:,i] = filters.gaussian_filter(im1[:,:,i],10)
im222 = uint8(im222)
figure()
subplot(1,3,1),imshow(im2),title('gaussian=2')
subplot(1,3,2),imshow(im22),title('gaussian=5')
subplot(1,3,3),imshow(im222),title('gaussian=10')
show()

到这里，python+OpenCV就算安装测试好了。