对于 ResNet 残差网络的思考——残差网络可以解决梯度消失的原因
对于 ResNet 残差网络的思考——残差网络可以解决梯度消失的原因
- 导言:
- 1.问题:
- 2.计算图:
- 2.1 求导链式法则的图形化表示
- 2.2 全链接网络 反向传播计算图
- 2.2 全链接网络 正向传播计算图
- 3. relu 和 ResNet 各自解决了什么问题
- 3.1 relu 解决梯度分布不均匀
- 3.2 ResNet 解决梯度整体变小
- 4.小结
导言:
从神经网络的历史上来看,深层网络由于梯度消失无法训练这个问题目前为止一共有两次很大的突破。第一次是神经网络开山鼻祖 Hinton 先生提出的 r e l u relu relu 激活函数取代了原来的 s i g m o i d sigmoid sigmoid 和 t a n h tanh tanh 函数,使得对于激活函数的导数变为了 1 1 1 。第二次是 何凯明 大神在 2015 年的论文 Deep Residual Learning for Image Recognition 中使用残差模块利用 shortcut 解决了深层网络梯度消失的问题,使得训练数百层甚至数千层的网络成为了可能。
深入思考了 ResNet 残差网络是如何解决梯度消失问题的,同时本文也对神经网络反向传播的计算提出了一种计算图,方便在以后研究过程中,可以通过直接看图,来了解在所构建的神经网络在反向传播过程中的具体细节。
1.问题:
最近读神经网络文章时遇到了一个问题。一开始神经网络使用 s i g m o i d sigmoid sigmoid 以及 t a n h tanh tanh 函数,如下图所示为 s i g m o i d sigmoid sigmoid 以及 t a n h tanh tanh 函数及其导数示意图。
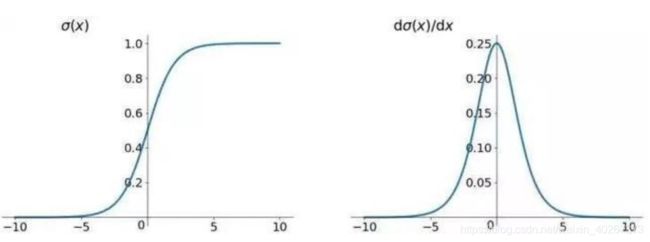

这种激活函数正如网上的大多数博文所说的一样,由于其导数在大部分区域内小于 1 1 1,会使得多层网络在反向传播时很多个小于1的导数不断相乘最后使得梯度越来越小,反向传播最后到输入层附近时几乎不更新。
历史上,深度学习开山祖师 Hinton 为了解决这个问题提出了一种新的激活函数就是 r e l u relu relu,它的函数及其导数图如下所示。
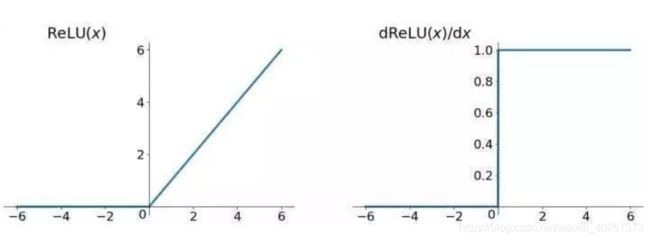
可以看到这种激活函数的导数在大于 0 0 0 的时候恒为1,这样就不会出现小于 1 1 1 的导数不断相乘导致梯度消失的问题。
按道理来说,梯度消失的问题就已经解决了呀,Happy Ending 本文完。但梯度消失的故事才刚刚开始 -_-!。即使有了 r e l u relu relu 这一大神器之后,梯度消失的问题也曾一度将深度学习开山鼻祖 Hinton 先生逼到一层一层的训练其在 Science 提出的自编码器(auto-encoder)。这也是我一直困惑的问题,都有了 r e l u relu relu 激活函数解决梯度消失问题了,那后面 何凯明 大神提出来的 ResNet 为什么又将梯度消失问题解决了一遍?什么意思只用 r e l u relu relu 激活函数为什么不能训练深层网络呀?毕竟 r e l u relu relu 激活函数的导数都是 1 1 1 呀,问题出在了哪里?
2.计算图:
为了更深入的理解这个问题。
PS: 而不是像其他分析 ResNet 残差网络的博文那样直接说残差网络通过引入恒等映射,恒等映射求导是 1 1 1 解决了梯度消失的问题。其实想想也知道这个解释不靠谱,因为 r e l u relu relu 在大于 0 的时候也是恒等映射。那不是说 ResNet 残差网络是多余的吗。
我创造了一种能够清楚表示神经网络反向传播时计算细节以及正向传播计算细节的计算图。
2.1 求导链式法则的图形化表示
在开始画出神经网络的计算图之前,我们首先来用计算图画出 高等数学 中经常会用到的多元函数求导链式法则。这也是神经网络反向传播算法的基础。
对于多元函数求导链式法则来说,其数学表示式如下:
∂ F ∂ x = ∂ F ∂ m ∂ m ∂ x + ∂ F ∂ n ∂ n ∂ x \frac{\partial F}{\partial x}=\frac{\partial F}{\partial m}\frac{\partial m}{\partial x}+\frac{\partial F}{\partial n}\frac{\partial n}{\partial x} ∂x∂F=∂m∂F∂x∂m+∂n∂F∂x∂n
其中 m,n 为中间变元。这样一个求导链式法则可以用如下的图形化的语言描述
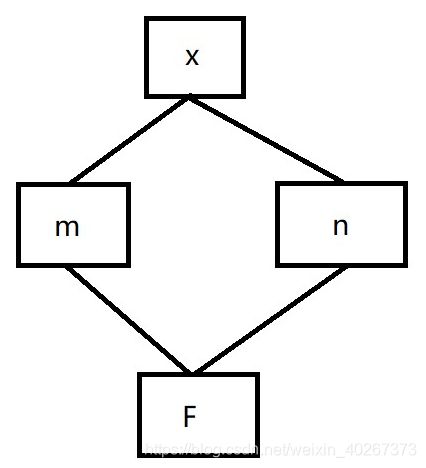
可以看到从 F F F 走到 x x x 一共有两条路,可以先由 F F F 走到 m m m 最终到 x x x,也可以选择中间经过 n n n 到 x x x。两种不同路径的选择用加号 + + + 相加,从 F F F 走到 m m m 用 ∂ F ∂ m \frac{\partial F}{\partial m} ∂m∂F 表示,从 m m m 走到 x x x 用 ∂ m ∂ x \frac{\partial m}{\partial x} ∂x∂m 表示。同一条路径的先后次序用乘号 × \times × 相乘。由此可以得到上面的数学表达式。同时我们使用方框来表示各个变量,由此来和神经网络示意图中表示神经元的符号 圆圈 相区分。
2.2 全链接网络 反向传播计算图
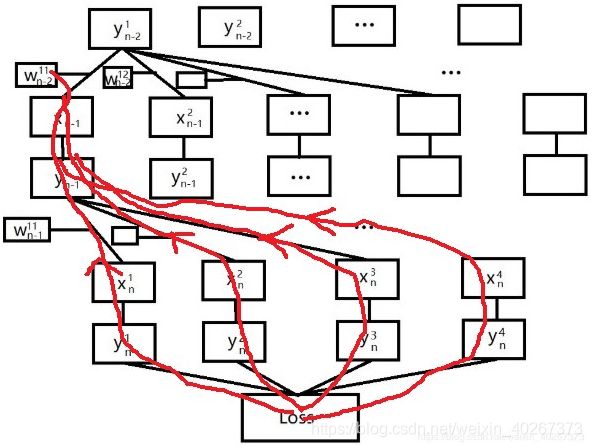
如下图所示,左边是一个全链接神经网络示意图,右边是一个全链接网络 计算图。由于在电脑上画图实在太难画了,我没有将它补充完整。

由此我们可以直接通过看图来得到反向传播过程中权重是如何具体更新的。
比如 图中的权重 w n − 1 11 w^{11}_{n-1} wn−111 来说,我们可以通过看图很容易写出它反向传播更新时的数学表达式。
∂ L o s s ∂ w n − 1 11 = ∂ L o s s ∂ y n 1 ∂ y n 1 ∂ x n 1 ∂ x n 1 ∂ w n − 1 11 \frac{\partial Loss}{\partial w^{11}_{n-1}}=\frac{\partial Loss}{\partial y^{1}_{n}}\frac{\partial y^{1}_{n}}{\partial x^{1}_{n}}\frac{\partial x^{1}_{n}}{\partial w^{11}_{n-1}} ∂wn−111∂Loss=∂yn1∂Loss∂xn1∂yn1∂wn−111∂xn1
其在图中的意义为:从 L o s s Loss Loss 出发走到 w n − 1 11 w^{11}_{n-1} wn−111 只有一条路,它从 L o s s Loss Loss 出发经过 y n 1 y^{1}_{n} yn1 再经过 x n 1 x^{1}_{n} xn1 即可到达 w n − 1 11 w^{11}_{n-1} wn−111。
同时在上图的表示中我们可以看到这样的三叉路口一样的图形。
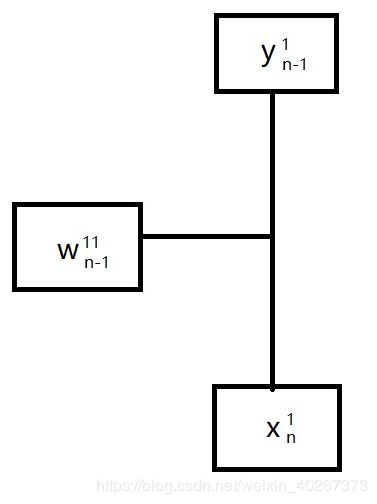
它在正向传播计算中表示加权求和,但是在反向传播计算图中的规则更为简单,满足以下关系。
∂ x n 1 ∂ w n − 1 11 = y n − 1 1 \frac{\partial x^{1}_{n}}{\partial w^{11}_{n-1}}=y^{1}_{n-1} ∂wn−111∂xn1=yn−11
∂ x n 1 ∂ y n − 1 1 = w n − 1 11 \frac{\partial x^{1}_{n}}{\partial y^{1}_{n-1}}=w^{11}_{n-1} ∂yn−11∂xn1=wn−111
表示从 x n 1 x_{n}^{1} xn1 走到 w n − 1 11 w^{11}_{n-1} wn−111 的结果为 y n − 1 1 y^{1}_{n-1} yn−11,从 x n 1 x_{n}^{1} xn1 走到 y n − 1 1 y^{1}_{n-1} yn−11 的结果为 w n − 1 11 w^{11}_{n-1} wn−111。
同样,我们也可以通过直接看计算图。 从图中我们可以看到从 L o s s Loss Loss 走到 w n − 2 11 w^{11}_{n-2} wn−211 存在着多条不同路径, y n 1 y^{1}_{n} yn1、 y n 2 y^{2}_{n} yn2、 y n 3 y^{3}_{n} yn3、 y n 4 y^{4}_{n} yn4 所代表的路径都可能,如下图红色线条所示。
由此我们可以得到 权重 w n − 2 11 w^{11}_{n-2} wn−211 反向传播时的数学表达式。
∂ L o s s ∂ w n − 2 11 = ∂ L o s s ∂ y n 1 ∂ y n 1 ∂ x n 1 ∂ x n 1 ∂ y n − 1 1 ∂ y n − 1 1 ∂ x n − 1 1 ∂ x n − 1 1 ∂ w n − 2 11 + ∂ L o s s ∂ y n 2 ∂ y n 2 ∂ x n 2 ∂ x n 2 ∂ y n − 1 1 ∂ y n − 1 1 ∂ x n − 1 1 ∂ x n − 1 1 ∂ w n − 2 11 + ∂ L o s s ∂ y n 3 ∂ y n 3 ∂ x n 3 ∂ x n 3 ∂ y n − 1 1 ∂ y n − 1 1 ∂ x n − 1 1 ∂ x n − 1 1 ∂ w n − 2 11 + ∂ L o s s ∂ y n 4 ∂ y n 4 ∂ x n 4 ∂ x n 4 ∂ y n − 1 1 ∂ y n − 1 1 ∂ x n − 1 1 ∂ x n − 1 1 ∂ w n − 2 11 \frac{\partial Loss}{\partial w^{11}_{n-2}}= \frac{\partial Loss}{\partial y^{1}_{n}}\frac{\partial y^{1}_{n}}{\partial x^{1}_{n}}\frac{\partial x^{1}_{n}}{\partial y^{1}_{n-1}}\frac{\partial y^{1}_{n-1}}{\partial x^{1}_{n-1}}\frac{\partial x^{1}_{n-1}}{\partial w^{11}_{n-2}} \\+\frac{\partial Loss}{\partial y^{2}_{n}}\frac{\partial y^{2}_{n}}{\partial x^{2}_{n}}\frac{\partial x^{2}_{n}}{\partial y^{1}_{n-1}}\frac{\partial y^{1}_{n-1}}{\partial x^{1}_{n-1}}\frac{\partial x^{1}_{n-1}}{\partial w^{11}_{n-2}} \\+\frac{\partial Loss}{\partial y^{3}_{n}}\frac{\partial y^{3}_{n}}{\partial x^{3}_{n}}\frac{\partial x^{3}_{n}}{\partial y^{1}_{n-1}}\frac{\partial y^{1}_{n-1}}{\partial x^{1}_{n-1}}\frac{\partial x^{1}_{n-1}}{\partial w^{11}_{n-2}} \\+\frac{\partial Loss}{\partial y^{4}_{n}}\frac{\partial y^{4}_{n}}{\partial x^{4}_{n}}\frac{\partial x^{4}_{n}}{\partial y^{1}_{n-1}}\frac{\partial y^{1}_{n-1}}{\partial x^{1}_{n-1}}\frac{\partial x^{1}_{n-1}}{\partial w^{11}_{n-2}} ∂wn−211∂Loss=∂yn1∂Loss∂xn1∂yn1∂yn−11∂xn1∂xn−11∂yn−11∂wn−211∂xn−11+∂yn2∂Loss∂xn2∂yn2∂yn−11∂xn2∂xn−11∂yn−11∂wn−211∂xn−11+∂yn3∂Loss∂xn3∂yn3∂yn−11∂xn3∂xn−11∂yn−11∂wn−211∂xn−11+∂yn4∂Loss∂xn4∂yn4∂yn−11∂xn4∂xn−11∂yn−11∂wn−211∂xn−11
使用 r e l u relu relu 函数 以及使用上面的三叉路口的化简方法,我们可以得到。
∂ L o s s ∂ w n − 1 11 = ∂ L o s s ∂ y n 1 y n − 1 1 \frac{\partial Loss}{\partial w^{11}_{n-1}}=\frac{\partial Loss}{\partial y^{1}_{n}}y^{1}_{n-1} ∂wn−111∂Loss=∂yn1∂Lossyn−11
∂ L o s s ∂ w n − 2 11 = ∂ L o s s ∂ y n 1 w n − 1 11 y n − 2 1 + ∂ L o s s ∂ y n 2 w n − 1 12 y n − 2 1 + ∂ L o s s ∂ y n 3 w n − 1 13 y n − 2 1 + ∂ L o s s ∂ y n 4 w n − 1 14 y n − 2 1 \frac{\partial Loss}{\partial w^{11}_{n-2}}= \frac{\partial Loss}{\partial y^{1}_{n}}w^{11}_{n-1}y^{1}_{n-2} \\+\frac{\partial Loss}{\partial y^{2}_{n}}w^{12}_{n-1}y^{1}_{n-2} \\+\frac{\partial Loss}{\partial y^{3}_{n}}w^{13}_{n-1}y^{1}_{n-2} \\+\frac{\partial Loss}{\partial y^{4}_{n}}w^{14}_{n-1}y^{1}_{n-2} ∂wn−211∂Loss=∂yn1∂Losswn−111yn−21+∂yn2∂Losswn−112yn−21+∂yn3∂Losswn−113yn−21+∂yn4∂Losswn−114yn−21
上面式子中的 y n − 1 1 y^{1}_{n-1} yn−11, y n − 2 1 y^{1}_{n-2} yn−21 需要通过正向传播计算得到。下面我们利用计算图来计算正向传播的结果。
2.2 全链接网络 正向传播计算图
下面我们再来看看如何利用我们刚才画出的计算图来计算正向传播过程。

非常惊讶的是只需要将前面的求偏导操作替换成乘法即可在计算图中完成正向传播的操作。和反向传播一样,在计算图中计算正向传播也是一个寻找路径的过程不同路径的结果应当相加。
下面我们利用计算图来完成 y n − 1 1 y^{1}_{n-1} yn−11, y n − 2 1 y^{1}_{n-2} yn−21 的计算(这里将 y n − 2 y_{n-2} yn−2 当做输入)。所以 y n − 2 1 y^{1}_{n-2} yn−21 就是其本身。而 y n − 1 1 y^{1}_{n-1} yn−11 的计算图路径如下所示。
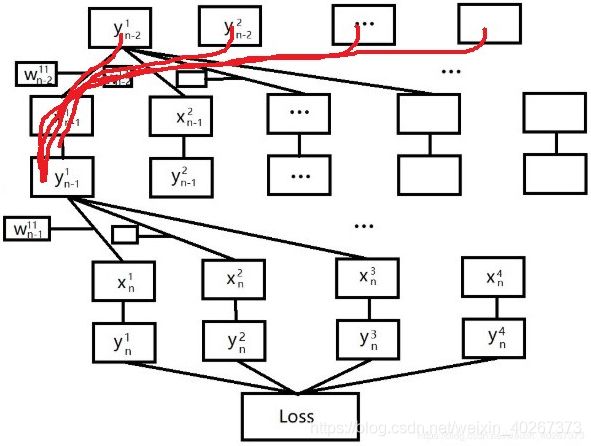
最后得到的 y n − 1 1 y^{1}_{n-1} yn−11
y n − 1 1 = w n − 2 11 y n − 2 1 + w n − 2 21 y n − 2 2 + w n − 2 31 y n − 2 3 + w n − 2 41 y n − 2 4 y^{1}_{n-1} = w^{11}_{n-2}y^{1}_{n-2}+w^{21}_{n-2}y^{2}_{n-2}+w^{31}_{n-2}y^{3}_{n-2}+w^{41}_{n-2}y^{4}_{n-2} yn−11=wn−211yn−21+wn−221yn−22+wn−231yn−23+wn−241yn−24
最后得到的梯度计算结果为
∂ L o s s ∂ w n − 1 11 = ∂ L o s s ∂ y n 1 ( w n − 2 11 y n − 2 1 + w n − 2 21 y n − 2 2 + w n − 2 31 y n − 2 3 + w n − 2 41 y n − 2 4 ) \frac{\partial Loss}{\partial w^{11}_{n-1}}=\frac{\partial Loss}{\partial y^{1}_{n}}(w^{11}_{n-2}y^{1}_{n-2}+w^{21}_{n-2}y^{2}_{n-2}+w^{31}_{n-2}y^{3}_{n-2}+w^{41}_{n-2}y^{4}_{n-2}) ∂wn−111∂Loss=∂yn1∂Loss(wn−211yn−21+wn−221yn−22+wn−231yn−23+wn−241yn−24)
∂ L o s s ∂ w n − 2 11 = ∂ L o s s ∂ y n 1 w n − 1 11 y n − 2 1 + ∂ L o s s ∂ y n 2 w n − 1 12 y n − 2 1 + ∂ L o s s ∂ y n 3 w n − 1 13 y n − 2 1 + ∂ L o s s ∂ y n 4 w n − 1 14 y n − 2 1 \frac{\partial Loss}{\partial w^{11}_{n-2}}= \frac{\partial Loss}{\partial y^{1}_{n}}w^{11}_{n-1}y^{1}_{n-2} \\+\frac{\partial Loss}{\partial y^{2}_{n}}w^{12}_{n-1}y^{1}_{n-2} \\+\frac{\partial Loss}{\partial y^{3}_{n}}w^{13}_{n-1}y^{1}_{n-2} \\+\frac{\partial Loss}{\partial y^{4}_{n}}w^{14}_{n-1}y^{1}_{n-2} ∂wn−211∂Loss=∂yn1∂Losswn−111yn−21+∂yn2∂Losswn−112yn−21+∂yn3∂Losswn−113yn−21+∂yn4∂Losswn−114yn−21
3. relu 和 ResNet 各自解决了什么问题
由于我们可以从 计算图 中很容易得到 权重更新的数学计算式。我们可以很清晰地思考 r e l u relu relu 激活函数和 ResNet 残差网络分别解决了什么问题。
3.1 relu 解决梯度分布不均匀
对于 r e l u relu relu 来说主要是使得 激活函数 的导数为 1 1 1, 从 上面的 梯度计算图中来说是使得下面这一类的路径的导数为 1 1 1 ,即直接变为一条直线。
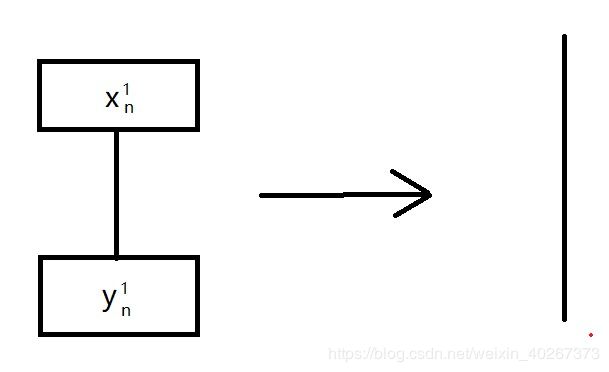
即对于没有死掉的神经元来说 ∂ y n 1 ∂ x n 1 = 1 \frac{\partial y^{1}_{n}}{\partial x^{1}_{n}}=1 ∂xn1∂yn1=1,对于死掉的神经元(relu dead) ∂ y n 1 ∂ x n 1 = 0 \frac{\partial y^{1}_{n}}{\partial x^{1}_{n}}=0 ∂xn1∂yn1=0 直接从求和计算中去掉。
由此我们可以简化上面的 w n − 1 11 w^{11}_{n-1} wn−111 和 w n − 2 11 w^{11}_{n-2} wn−211 的数学计算式。
∂ L o s s ∂ w n − 1 11 = ∂ L o s s ∂ y n 1 ∂ x n 1 ∂ w n − 1 11 \frac{\partial Loss}{\partial w^{11}_{n-1}}=\frac{\partial Loss}{\partial y^{1}_{n}}\frac{\partial x^{1}_{n}}{\partial w^{11}_{n-1}} ∂wn−111∂Loss=∂yn1∂Loss∂wn−111∂xn1
∂ L o s s ∂ w n − 2 11 = ∂ L o s s ∂ y n 1 ∂ x n 1 ∂ y n − 1 1 ∂ x n − 1 1 ∂ w n − 2 11 + ∂ L o s s ∂ y n 2 ∂ x n 2 ∂ y n − 1 1 ∂ x n − 1 1 ∂ w n − 2 11 + ∂ L o s s ∂ y n 3 ∂ x n 3 ∂ y n − 1 1 ∂ x n − 1 1 ∂ w n − 2 11 + ∂ L o s s ∂ y n 4 ∂ x n 4 ∂ y n − 1 1 ∂ x n − 1 1 ∂ w n − 2 11 \frac{\partial Loss}{\partial w^{11}_{n-2}}= \frac{\partial Loss}{\partial y^{1}_{n}}\frac{\partial x^{1}_{n}}{\partial y^{1}_{n-1}}\frac{\partial x^{1}_{n-1}}{\partial w^{11}_{n-2}} \\+\frac{\partial Loss}{\partial y^{2}_{n}}\frac{\partial x^{2}_{n}}{\partial y^{1}_{n-1}}\frac{\partial x^{1}_{n-1}}{\partial w^{11}_{n-2}} \\+\frac{\partial Loss}{\partial y^{3}_{n}}\frac{\partial x^{3}_{n}}{\partial y^{1}_{n-1}}\frac{\partial x^{1}_{n-1}}{\partial w^{11}_{n-2}} \\+\frac{\partial Loss}{\partial y^{4}_{n}}\frac{\partial x^{4}_{n}}{\partial y^{1}_{n-1}}\frac{\partial x^{1}_{n-1}}{\partial w^{11}_{n-2}} ∂wn−211∂Loss=∂yn1∂Loss∂yn−11∂xn1∂wn−211∂xn−11+∂yn2∂Loss∂yn−11∂xn2∂wn−211∂xn−11+∂yn3∂Loss∂yn−11∂xn3∂wn−211∂xn−11+∂yn4∂Loss∂yn−11∂xn4∂wn−211∂xn−11
同时使用上面我们提到的三叉路口的化简方法
我们可以得到如下非常优美的式子
∂ L o s s ∂ w n − 1 11 = ∂ L o s s ∂ y n 1 y n − 1 1 \frac{\partial Loss}{\partial w^{11}_{n-1}}=\frac{\partial Loss}{\partial y^{1}_{n}}y^{1}_{n-1} ∂wn−111∂Loss=∂yn1∂Lossyn−11
∂ L o s s ∂ w n − 2 11 = ∂ L o s s ∂ y n 1 w n − 1 11 y n − 2 1 + ∂ L o s s ∂ y n 2 w n − 1 12 y n − 2 1 + ∂ L o s s ∂ y n 3 w n − 1 13 y n − 2 1 + ∂ L o s s ∂ y n 4 w n − 1 14 y n − 2 1 \frac{\partial Loss}{\partial w^{11}_{n-2}}= \frac{\partial Loss}{\partial y^{1}_{n}}w^{11}_{n-1}y^{1}_{n-2} \\+\frac{\partial Loss}{\partial y^{2}_{n}}w^{12}_{n-1}y^{1}_{n-2} \\+\frac{\partial Loss}{\partial y^{3}_{n}}w^{13}_{n-1}y^{1}_{n-2} \\+\frac{\partial Loss}{\partial y^{4}_{n}}w^{14}_{n-1}y^{1}_{n-2} ∂wn−211∂Loss=∂yn1∂Losswn−111yn−21+∂yn2∂Losswn−112yn−21+∂yn3∂Losswn−113yn−21+∂yn4∂Losswn−114yn−21
此后通过正向传播计算得到最后的梯度计算结果为
∂ L o s s ∂ w n − 1 11 = ∂ L o s s ∂ y n 1 ( w n − 2 11 y n − 2 1 + w n − 2 21 y n − 2 2 + w n − 2 31 y n − 2 3 + w n − 2 41 y n − 2 4 ) \frac{\partial Loss}{\partial w^{11}_{n-1}}=\frac{\partial Loss}{\partial y^{1}_{n}}(w^{11}_{n-2}y^{1}_{n-2}+w^{21}_{n-2}y^{2}_{n-2}+w^{31}_{n-2}y^{3}_{n-2}+w^{41}_{n-2}y^{4}_{n-2}) ∂wn−111∂Loss=∂yn1∂Loss(wn−211yn−21+wn−221yn−22+wn−231yn−23+wn−241yn−24)
∂ L o s s ∂ w n − 2 11 = ∂ L o s s ∂ y n 1 w n − 1 11 y n − 2 1 + ∂ L o s s ∂ y n 2 w n − 1 12 y n − 2 1 + ∂ L o s s ∂ y n 3 w n − 1 13 y n − 2 1 + ∂ L o s s ∂ y n 4 w n − 1 14 y n − 2 1 \frac{\partial Loss}{\partial w^{11}_{n-2}}= \frac{\partial Loss}{\partial y^{1}_{n}}w^{11}_{n-1}y^{1}_{n-2} \\+\frac{\partial Loss}{\partial y^{2}_{n}}w^{12}_{n-1}y^{1}_{n-2} \\+\frac{\partial Loss}{\partial y^{3}_{n}}w^{13}_{n-1}y^{1}_{n-2} \\+\frac{\partial Loss}{\partial y^{4}_{n}}w^{14}_{n-1}y^{1}_{n-2} ∂wn−211∂Loss=∂yn1∂Losswn−111yn−21+∂yn2∂Losswn−112yn−21+∂yn3∂Losswn−113yn−21+∂yn4∂Losswn−114yn−21
可以从上述最后的梯度计算结果中看到,通过使用 r e l u relu relu 函数使得不同网络不同深度处的梯度形式相近,不会出现随着反向传播的进行越往后面梯度越小。
但为什么留下来的这个简洁的式子仍然有梯度消失的问题呢?
3.2 ResNet 解决梯度整体变小
我们接着分析上面得到最后的梯度计算结果,可以看到其中有很多权重因子。这是因为在 计算图 中经过了 如下的权重层导致有多条路径可以选择的结果。由于上述计算过程同时设计正向传播和反向传播会贯穿整个网络,导致网络越深,最后的梯度计算结果中前面乘上的权重系数也会越来越多。

我们可以简单分析一下上面得到的最终计算 w n − 2 11 w^{11}_{n-2} wn−211 以及 w n − 1 11 w^{11}_{n-1} wn−111 梯度的计算式
∂ L o s s ∂ w n − 1 11 = ∂ L o s s ∂ y n 1 ( w n − 2 11 y n − 2 1 + w n − 2 21 y n − 2 2 + w n − 2 31 y n − 2 3 + w n − 2 41 y n − 2 4 ) \frac{\partial Loss}{\partial w^{11}_{n-1}}=\frac{\partial Loss}{\partial y^{1}_{n}}(w^{11}_{n-2}y^{1}_{n-2}+w^{21}_{n-2}y^{2}_{n-2}+w^{31}_{n-2}y^{3}_{n-2}+w^{41}_{n-2}y^{4}_{n-2}) ∂wn−111∂Loss=∂yn1∂Loss(wn−211yn−21+wn−221yn−22+wn−231yn−23+wn−241yn−24)
∂ L o s s ∂ w n − 2 11 = ∂ L o s s ∂ y n 1 w n − 1 11 y n − 2 1 + ∂ L o s s ∂ y n 2 w n − 1 12 y n − 2 1 + ∂ L o s s ∂ y n 3 w n − 1 13 y n − 2 1 + ∂ L o s s ∂ y n 4 w n − 1 14 y n − 2 1 \frac{\partial Loss}{\partial w^{11}_{n-2}}= \frac{\partial Loss}{\partial y^{1}_{n}}w^{11}_{n-1}y^{1}_{n-2} \\+\frac{\partial Loss}{\partial y^{2}_{n}}w^{12}_{n-1}y^{1}_{n-2} \\+\frac{\partial Loss}{\partial y^{3}_{n}}w^{13}_{n-1}y^{1}_{n-2} \\+\frac{\partial Loss}{\partial y^{4}_{n}}w^{14}_{n-1}y^{1}_{n-2} ∂wn−211∂Loss=∂yn1∂Losswn−111yn−21+∂yn2∂Losswn−112yn−21+∂yn3∂Losswn−113yn−21+∂yn4∂Losswn−114yn−21
我们可以看到通过 r e l u relu relu 解决反向传播时梯度衰减问题后,不同深度的权重感受到的梯度形式相近。不会出现一开始有梯度,而反向传播到后面的层就感受不到梯度了。但是随着网络深度的增加上面的式子有什么问题呢?
结果是前面乘的权重系数会越来越多。因为不管是正向传播还是反向传播,每条路径经过一个权重因子都会乘上这个权重因子。随着层数的增加,路径变得越来越长,在这条路上走一走遇到的权重因子也会越来越多,梯度会整体的变小。
也就是说网络变深了,梯度虽然每层的相同但是整体变小了。如果网络足够深,每一层的梯度都变小到感受不到了。这也就是当初 Hinton 祖师爷虽然用 r e l u relu relu 这个神器解决了梯度分布不均匀的问题,但是却留下了一个更大的问题,权重分布是均匀了但是整体变小了-_-)?
那么 2015 年横空出世的 ResNet 是如何解决这一问题的呢?
ResNet 的解决方法非常粗暴,就是加入 shortcut 。这个 shortcut 在梯度计算图中相当于增加了一条可以跳过权重的层的路径。使得最终计算所得的权重处的梯度 加上一项 没有经过权重层衰减的梯度。话不多说,下面我们就画一画 ResNet 残差网络中的一个残差模块的 计算图。
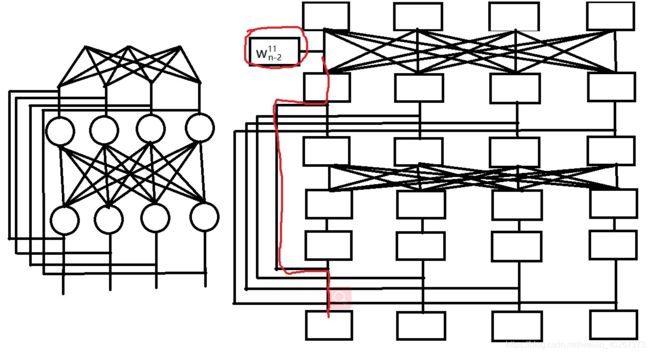
可以看到同样我们计算 w n − 2 11 w^{11}_{n-2} wn−211 处的梯度。相比于此前的 计算图 ,由于 ResNet 残差模块中加入了 shortcut 导致 梯度计算图中出现了一条可以不用经过中间的权重层的捷径(如图红色的线条所示)。这解决了经过权重层梯度消失的问题。
同样对于正向传播来说这样的 shortcut 也增加一条跳过权重层的路径,由于最后的结果是不同路径相加,所以即使其他路径足够小也没什么,梯度也没整体减少。
4.小结
从上面对于 计算图 的分析中,我们可以看出在神经网络反向传播过程中,一共有两个因素会导致梯度消失问题。一是激活函数导数小于 1 1 1,二是经过权重层。前者会导致反向传播过程中越往后传播梯度越小梯度分布不均匀,后者会导致随着网络深度的增加每一层的梯度都整体减少。 r e l u relu relu 函数解决了第一个问题,而 ResNet 解决了第二个问题。
同时上面提出的 计算图 使得我们可以方便的了解神经网络反向传播过程中的具体细节。