【UVA11997】K Smallest Sums 优先队列的多路归并问题

背景

给你个有序列表(假设非降序),将其合并为一个列表(这为《算法导论》上堆部分一道例题)

一种策略是建立一个大小为的小根堆,每个序列第一个元素入堆,标记每个元素所属队列.

依次取出,取出后若对应序列还有元素,则加入堆中否则不加入或者加入.

PS:归并排序的归并过程就可以看作是大小为的一个小根堆进行合并的操作.

---

问题

有个序列，每个序列有个元素。现在要在每个序列里选一个元素出来求和,故有个和，求元素总和前小的值

 

分析

首先考虑两个序列的情况(下面默认每个序列已排非降序)

会组合成种和,我们注意到最小值一定为,而第二小值为或

我们可以发现若第小值为那么第小值为或者

粗略的,我们建立一个优先队列,队列中初始含

第次提取堆顶得第小值,再把加入.则可以保证下一次获得第小值.

 

我们可以进行扩展:

第次提取小值,那么将加入

下一次可以获得第小值

但我们可以看到这样粗略的加入会产生两个问题:

• 一次扩展元素过多,如要找第小值,最后堆中元素可能有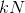个
• 相同元素重复入堆的判断,如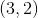会来自.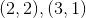

 

我们重新考虑两个序列,并结合路归并,我们将那个和以为主元写成如下形式:

我们这就变为了路归并问题,堆的大小也稳定在,也不会有重复元素入堆,时间复杂度为

 

接下来的问题就是考虑如何将个序列向多个序列进行转换

注意到:由于我们要求前小的值,而从构成个序列前小的值一定是

两个序列前小的值与进行合并

于是就可以合并得到前小的值,再与进行合并

故问题可以通过次合并解决,时间复杂度为

 

#include 
#include 
#include 
#include 
#include 
using namespace std;

int N;
int A[1005][1005];
struct node {
  int val, id;
  node(int val, int id) : val(val), id(id){
  };
};
struct cmp {
  bool operator ()(const node &a, const node &b){
    return a.val > b.val;
  }
};
void Merge(int *, int *, int *);

int main(){
  while(~scanf("%d", &N)){
    int i, j;
    for(i = 1; i <= N; i++){
      for(j = 1; j <= N; j++)
        scanf("%d", &A[i][j]);
      sort(A[i] + 1, A[i] + 1 + N);
    }
    for(i = 2; i <= N; i++) Merge(A[1], A[i], A[1]);
    for(i = 1; i <= N; i++) printf("%d%c", A[1][i], (i == N) ? '\n' : ' ');
  }
  return 0;
}

void Merge(int *A, int *B, int *C){
  priority_queue, cmp> Q;
  int i;
  for(i = 1; i <= N; i++) Q.push(node(A[i] + B[1], 1));
  for(i = 1; i <= N; i++){
    auto item = Q.top(); Q.pop();
    C[i] = item.val;
    if(item.id + 1 <= N) Q.push(node(item.val - B[item.id] + B[item.id + 1], item.id + 1));
  }
}