基于LSTM和TextCNN的文本情感分析
Pipeline
LSTM
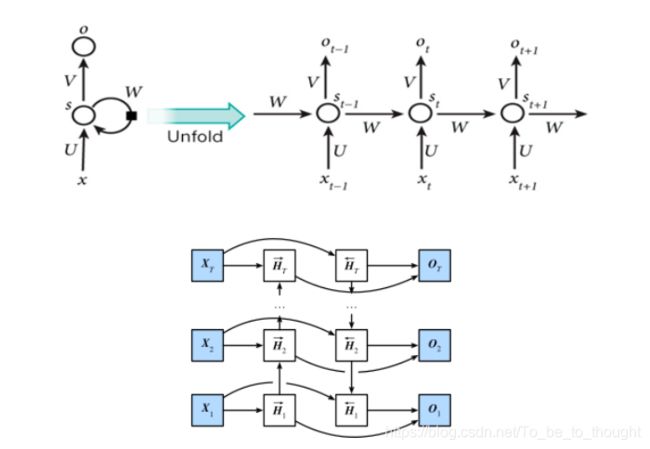
对于给定序列 { X 1 , X 2 , . . . , X T } \{ \boldsymbol X_1,\boldsymbol X_2,...,\boldsymbol X_T\} {X1,X2,...,XT},其中, X t ∈ R n × d \boldsymbol X_t \in R^{n \times d} Xt∈Rn×d为时间步 t t t的输入, n n n为批量大小, d d d为输入维度。在双向神经网络的架构中,时间步 t t t上的正向隐藏状态为 H t → ∈ R n × h \overrightarrow {\boldsymbol H_t} \in R^{n \times h} Ht∈Rn×h,正向隐藏状态维度为 h h h,反向隐藏状态为 H t ← ∈ R n × h \overleftarrow{\boldsymbol H_t} \in R^{n \times h} Ht∈Rn×h,则正向和反向隐藏状态的计算如下:
H t → = ϕ ( X t W x h f + H t − 1 → W h h f + b h f ) \overrightarrow {\boldsymbol H_t} = \phi(X_tW_{xh}^f+\overrightarrow {\boldsymbol H_{t-1}}W_{hh}^f +b_h^f) Ht=ϕ(XtWxhf+Ht−1Whhf+bhf)
H t ← = ϕ ( X t W x h b + H t + 1 ← W h h b + b h f ) \overleftarrow {\boldsymbol H_t} = \phi(X_t W_{xh}^b+\overleftarrow {\boldsymbol H_{t+1}}W_{hh}^b +b_h^f) Ht=ϕ(XtWxhb+Ht+1Whhb+bhf)
其中, W x h f ∈ R d × h W_{xh}^f \in R^{d \times h} Wxhf∈Rd×h, W h h f ∈ R h × h W_{hh}^f \in R^{h \times h} Whhf∈Rh×h, W x h b ∈ R d × h W_{xh}^b \in R^{d \times h} Wxhb∈Rd×h, W h h b ∈ R h × h W_{hh}^b \in R^{h \times h} Whhb∈Rh×h, b h b ∈ R 1 × h b_h^b \in R^{1 \times h} bhb∈R1×h, ϕ \phi ϕ为激活函数。
然后连接同一时间步上两个方向的隐藏状态$ \overrightarrow{ \boldsymbol H_t} 和 和 和\overleftarrow {\boldsymbol H_t} 得 到 得到 得到H_t \in R^{n \times 2h} , 并 将 其 输 入 到 输 出 层 , 输 出 层 计 算 出 ,并将其输入到输出层,输出层计算出 ,并将其输入到输出层,输出层计算出\boldsymbol O_t \in R^{ n \times q} ( 输 出 维 度 为 (输出维度为 (输出维度为h$):
O t = H t W h q + b q \boldsymbol O_t=\boldsymbol H_t \boldsymbol W_{hq}+ \boldsymbol b_q Ot=HtWhq+bq
其中, W h q ∈ R 2 h × q \boldsymbol W_{hq} \in R^{2h \times q} Whq∈R2h×q和偏差 b q ∈ R 1 × q \boldsymbol b_q \in R^{1 \times q} bq∈R1×q。
TextCNN
序列数据的卷积操作
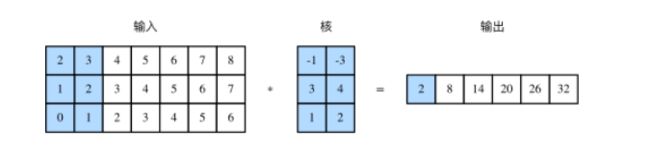
词向量的维度可以看成是输入通道数,序列方向可以看成这句话的特征。多输入通道的一维互相关运算可以看作单输入通道的二维互相关运算。反过来说,对于文本数据,当二维卷积核的高度等于输入的高度时才成立。
序列数据的池化操作(时序最大池化层)
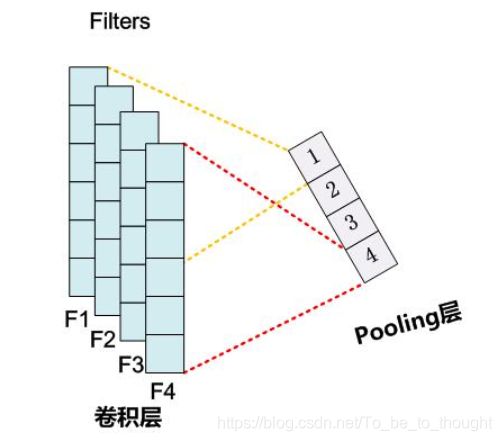
TextCNN 中使用的时序最大池化(max-over-time pooling)层实际上对应一维全局最大池化层:假设输入包含多个通道,各通道由不同时间步上的数值组成,各通道的输出即该通道所有时间步中最大的数值。因此,时序最大池化层的输入在各个通道上的时间步数可以不同。
TextCNN的数据流变化过程
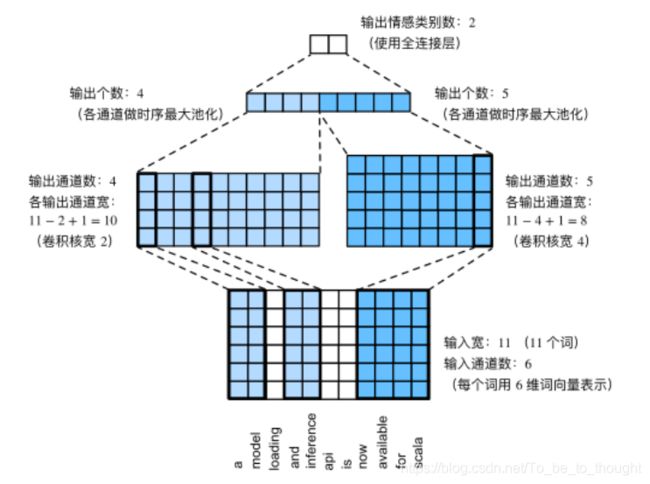
TextCNN 模型主要使用了一维卷积层和时序最大池化层。假设输入的文本序列由 n n n 个词组成,每个词用 d d d 维的词向量表示。那么输入样本的宽为 n n n,输入通道数为 d d d。TextCNN 的计算主要分为以下几步。
- 定义多个一维卷积核,并使用这些卷积核对输入分别做卷积计算。宽度不同的卷积核可能会捕捉到不同个数的相邻词的相关性。
- 对输出的所有通道分别做时序最大池化,再将这些通道的池化输出值连结为向量。
- 通过全连接层将连结后的向量变换为有关各类别的输出。这一步可以使用丢弃层应对过拟合。
代码如下:
class TextCNN(nn.Module):
def __init__(self, vocab, embed_size, kernel_sizes, num_channels):
'''
@params:
vocab: 在数据集上创建的词典,用于获取词典大小
embed_size: 嵌入维度大小
kernel_sizes: 卷积核大小列表
num_channels: 卷积通道数列表
'''
super(TextCNN, self).__init__()
self.embedding = nn.Embedding(len(vocab), embed_size) # 参与训练的嵌入层
self.constant_embedding = nn.Embedding(len(vocab), embed_size) # 不参与训练的嵌入层
self.pool = GlobalMaxPool1d() # 时序最大池化层没有权重,所以可以共用一个实例
self.convs = nn.ModuleList() # 创建多个一维卷积层
for c, k in zip(num_channels, kernel_sizes):
self.convs.append(nn.Conv1d(in_channels = 2*embed_size,
out_channels = c,
kernel_size = k))
self.decoder = nn.Linear(sum(num_channels), 2)
self.dropout = nn.Dropout(0.5) # 丢弃层用于防止过拟合
def forward(self, inputs):
'''
@params:
inputs: 词语下标序列,形状为 (batch_size, seq_len) 的整数张量
@return:
outputs: 对文本情感的预测,形状为 (batch_size, 2) 的张量
'''
embeddings = torch.cat((
self.embedding(inputs),
self.constant_embedding(inputs)), dim=2) # (batch_size, seq_len, 2*embed_size)
# 根据一维卷积层要求的输入格式,需要将张量进行转置
embeddings = embeddings.permute(0, 2, 1) # (batch_size, 2*embed_size, seq_len)
encoding = torch.cat([
self.pool(F.relu(conv(embeddings))).squeeze(-1) for conv in self.convs], dim=1)
# encoding = []
# for conv in self.convs:
# out = conv(embeddings) # (batch_size, out_channels, seq_len-kernel_size+1)
# out = self.pool(F.relu(out)) # (batch_size, out_channels, 1)
# encoding.append(out.squeeze(-1)) # (batch_size, out_channels)
# encoding = torch.cat(encoding) # (batch_size, out_channels_sum)
# 应用丢弃法后使用全连接层得到输出
outputs = self.decoder(self.dropout(encoding))
return outputs
embed_size, kernel_sizes, nums_channels = 100, [3, 4, 5], [100, 100, 100]
net = TextCNN(vocab, embed_size, kernel_sizes, nums_channels)