HMM模型(Ⅰ)—原理与简用
HMM模型(Ⅰ)—原理与简用
- 引言
- HMM简绍
- 数学原理
- 符号约定
- 模型假设
- 模型可以解决的问题
- 解决问题的算法
- 前向-后向(forward-backward)算法
- Bawn-Welch算法(EM)
- 维特比(Viter)算法
- 简用
- 例子
- 求解程序与结果:
- 维特比算法计算最佳路径:
- Bawn-Welch算法估计参数
- 前向-后向(forward-backward)算法计算P(O|λ)
- 小结
- 参考文献
引言
最近几天,由于疫情的影响,笔者这几天宅家钻研数模中隐马尔可夫模型(HMM),于是将所学所想整理成学习笔记,遂成此文。
HMM简绍
关于HMM的介绍很多,笔者在此处的思想主要学习于李航老师所著的《统计学习方法》一书与一些博客大佬的文章。
什么是HMM?比如说生活中,会有很多事情发生,发生的事情的结果是可观的,利用数学的方法我们也可以计算其发生的概率,但是,有些事情发生,还有其背后的隐藏状态在作祟。
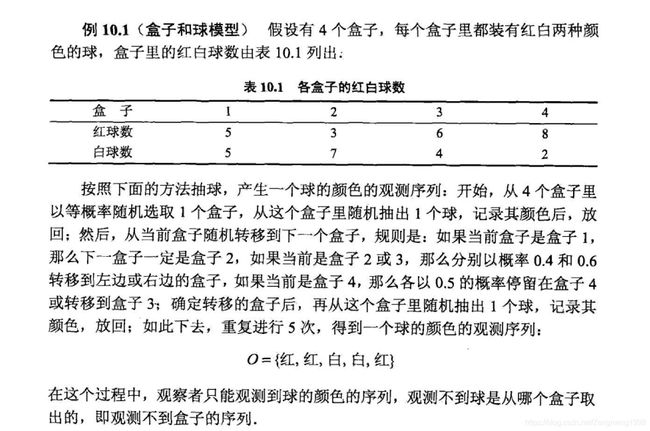
举个最经典的例子说:有3个箱子编号1、2、3号箱,3箱各放置一定数量的红球与白球,每次我们随机从箱子中取球,计入颜色后放回箱中,那么我们怎么来计算所取球色序列的发生概率呢?这时我们需要一个数学模型来计算其的概率,HMM模型便是用于解决此问题所作的一个数学模型。
数学原理
符号约定
模型假设
模型可以解决的问题
1、概率计算:已知A、B、pi求概率P(O|λ)
2、学习问题:给定O,估计A、B、pi的参数
3、预测(编码)问题:已知O、A、B、pi,求最优的I
解决问题的算法
前向-后向(forward-backward)算法
主要思想如笔者笔记所述:
前向算法:定义前向概率at(i):前都为O的序列,t时刻在qi状态的概率
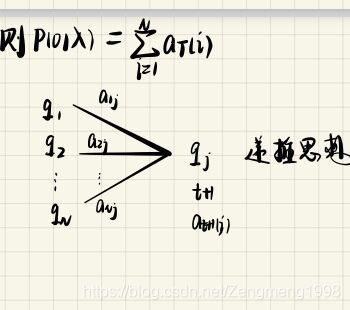
算法思想:

后向算法:
定义后向概率bt(i):t时刻(0t到T都是O序列下的事件)为状态qi的概率
算法思想:
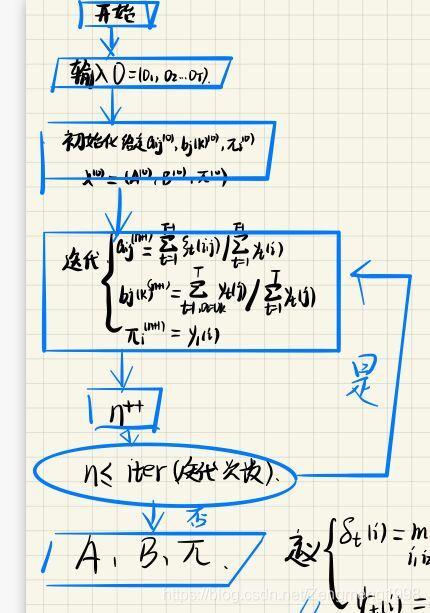
Bawn-Welch算法(EM)
维特比(Viter)算法
算法思想
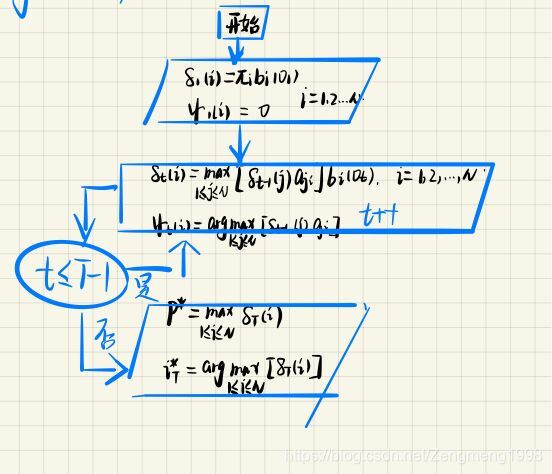
写在后面:
模型的数学原理讲述源自笔者个人的浅见,如有不明或请参照原著的详细讲解。
简用
例子源自李航老师所著的《统计学习方法》一书,实现工具选用的是python及其第三库hmmlearn:
例子
求解程序与结果:
首先定义好HMM模型的三要素
# 隐藏状态:4个盒子
states = ['box1', 'box2', 'box3','box4']
n_states = len(states)
# 观测状态:2种球
observations = ['red', 'white']
n_observations = len(observations)
# 模型参数
#初始概率分布
start_probability = np.array([0.25, 0.25, 0.25,0.25])
#概率转移矩阵
transition_probability = np.array([[0,1,0,0],[0.4,0, 0.6, 0],[0, 0.4,0, 0.6],[0,0,0.5,0.5]])
#观测分布矩阵
emission_probability = np.array([[0.5, 0.5],[0.3, 0.7],[0.6, 0.4],[0.8,0.2]])
调用第三方库进行求解计算:
# 用于离散观测状态
model = hmm.MultinomialHMM(n_components = n_states)
model.startprob_ = start_probability
model.transmat_ = transition_probability
model.emissionprob_ = emission_probability
维特比算法计算最佳路径:
# 维特比算法
seen = np.array([[0,0,1,1,0]]).T
logprob, box = model.decode(seen, algorithm='viterbi')
print(logprob)
print(np.array(states)[box])结果:
-6.24746192329327
['box4' 'box3' 'box2' 'box3' 'box4']
即:最佳路径为:['box4' 'box3' 'box2' 'box3' 'box4']
对应概率:exp(-6.24746192329327)Bawn-Welch算法估计参数
#B-W算法
model2 = hmm.MultinomialHMM(n_components=n_states, n_iter=20, tol=0.01)
X2 = np.array([[0,0,1,1,0]])
model2.fit(X2)
print('startprob_:', model2.startprob_)
print('transmat_':, model2.transmat_)
print('emissionprob:', model2.emissionprob_)
计算结果
初始状态概率
startprob_: [5.98479556e-53 2.63556559e-28 1.00000000e+00 2.79990233e-30]
状态转移矩阵
transmat_: [[5.25522859e-14 2.41571237e-23 6.89714885e-23 1.00000000e+00]
[9.99643444e-01 2.14478163e-67 3.48923494e-79 3.56556038e-04]
[2.48327760e-30 1.00000000e+00 1.32387087e-35 5.07754698e-30]
[4.33212339e-16 5.84359862e-01 4.15281391e-01 3.58746763e-04]]
状态观测矩阵
emissionprob: [[1.14796980e-22 1.00000000e+00]
[1.00000000e+00 2.57962471e-27]
[1.00000000e+00 1.25797699e-11]
[2.31782429e-06 9.99997682e-01]]前向-后向(forward-backward)算法计算P(O|λ)
#利用前后向算法计算X2的概率
print('score: ', model2.score(X2))
计算结果
score: -1.3863930415785406
P=exp(score)小结
HMM数学模型的理解并不难,现阶段笔者也拜读了一部分的关于HMM的文献、博客等,其在追求的精化的地方主要在用数学方法,亦或改进数学模型、亦或改进状态数的分析数量、可观测序列的选取,以求达到其模型预测的准确性,一般而言,若可观数为n,模型的预测的准确率若大于1/n,则该模型具有可取价值。对于HMM的应用价值,以上便为笔者现阶段的浅见。同时笔者存在的问题主要在模型解释,与python的hmmlearn库的熟练使用上,仍有提升之处。不足之处望读者多多指正。
参考文献
李航《统计学习方法》P171-P189