一、NumPy简介
NumPy是高性能科学计算和数据分析的基础包。它是pandas等其他各种工具的基础。
1、NumPy的主要功能
(1)ndarray:一个多维数组结构,高效且节省空间。
(2)无需循环对整组数据进行快速运算的数学函数。
(3)线性代数、随机数生成和傅里叶变换功能。
2、安装和引用
pip install numpy # 安装方法
import numpy as np # 引用方法3、为什么要使用NumPy?
(1)例:已知若干家跨国公司的市值(美元),将其换算为人民币
import numpy as np
import random
# uniform随机生成浮点数,这里是随机生成100~200之间的浮点数
a = [random.uniform(100.0, 200.0) for i in range(50)]
print(a)
x = 6.8 # 人民币和美元的汇率
# 方法一:使用循环
b = []
for ele in a:
b.append(ele * x)
print(b)
# 方法二:使用numpy
a = np.array(a)
c = a * x
print(c)(2)例:已知购物车中每件商品的价格和商品件数,求总金额
import numpy as np
import random
# uniform随机生成浮点数,这里是随机生成100~200之间的浮点数
a = [random.uniform(100.0, 200.0) for i in range(50)]
g = [random.randint(1, 10) for j in range(50)]
d = np.array(g)
sum = a*d.sum() # 所有商品总金额
print(sum)二、ndarray-多维数组对象
创建ndarray:np.array(array_like)
数组和列表的区别:
- 数组对象内的元素类型必须相同
- 数组大小不可修改
1、ndarray常用属性
| 属性 | 属性含义 |
|---|---|
| T | 数组的转置(对高维数组而言) |
| size | 数组元素的个数 |
| ndim | 数组的维数 |
| shape | 数组的维度大小(元组形式) |
| dtype | 数组元素的数据类型 |
(1)dtype
可以查看具体数据类型。
>>> import numpy as np
>>> a = np.array(range(10))
>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> a.dtype
dtype('int64')(2)size
查看当前存了多少个元素。
>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> a.size
10(3)ndim
查看数组的维数。
>>> a
array([[1, 2, 3],
[4, 5, 6]])
>>> a.ndim
2(3)shape
返回一个元组,说明当前数组对象是一个几行几列的多维数组。
>>> a = np.array([[1,2,3], [4,5,6]])
>>> a
array([[1, 2, 3],
[4, 5, 6]])
>>> a.dtype
dtype('int64')
>>> a.size
6
>>> a.shape
(2, 3) # 返回一个元组,说明是一个两行三列的二维数组
# 三维数组
>>> a = np.array([[[1,2,3], [4,5,6]],[[1,2,3], [3,4,5]]])
>>> a
array([[[1, 2, 3],
[4, 5, 6]],
[[1, 2, 3],
[3, 4, 5]]])
>>> a.shape # 两页两行三列的三维数组
(2, 2, 3)还可以使用reshape函数来调整数组大小
>>> a=np.arange(15)
>>> a
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14])
>>> a.reshape((3,5))
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]])查看获取对应位置元素
>>> a
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]])
>>> a[0][0]
0
>>> a[0,0]
0(4)T
数组转置。
>>> a = np.array([[1,2,3], [4,5,6]])
>>> a
array([[1, 2, 3],
[4, 5, 6]])
>>> a.T
array([[1, 4],
[2, 5],
[3, 6]])
>>> a = a.T
>>> a.T
array([[1, 2, 3],
[4, 5, 6]])
>>> _.T
array([[1, 4],
[2, 5],
[3, 6]])2、ndarray数据类型
ndarray中绝大多数情况下都是保存各种数字,基本不保存字符串数据。
| 类型 | 字节细分 |
|---|---|
| 布尔型 | bool_ |
| 整型 | int_ int8 int16 int32 int64 |
| 无符号整型 | uint8 uint16 uint32 uint64 |
| 浮点型 | float_ float16 float32 float64 |
| 复数型 | complex_ complex64 complex128 |
注意:
(1)64位的整数最大值是:263-1=9223372036854775807;
(2)无符号整型只表示正数,因此64位的无符号整数最大值是:264-1=18446744073709551615
3、ndarray对象创建
| 方法 | 描述 |
|---|---|
| array() | 将列表转换为数组,可选择显示指定dtype |
| arange() | range的numpy版,支持浮点数 |
| linespace() | 类似arange(),第三个参数为数组长度 |
| zeros() | 根据指定形状和dtype创建全0数组 |
| ones() | 根据指定形状和dtype创建全1数组 |
| empty() | 根据指定形状和dtype创建空数组(随机值) |
| eye() | 根据指定边长创建单位矩阵 |
(1)zeros、ones
zeros:生成值全为0的数组。
ones:生成值全为1的数组。
# 列表的方法
>>> np.array([0]*10)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0])
# zeros()方法
>>> np.zeros(10)
array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
>>> a = np.zeros(10)
>>> a.dtype
dtype('float64') # 默认计算是浮点数
# 设置类型参数
>>> a = np.zeros(10, dtype='int')
>>> a
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0])
# ones()方法生成全是全为1的数组
>>> a = np.ones(10)
>>> a
array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])(2)empty
根据指定形状和dtype创建空数组(随机数)。取到内存内留存的值。
可以先创建数组,再将这些值都覆盖掉。
>>> a = np.empty(100)
>>> a
array([ 2.00000000e+000, 2.00000000e+000, 2.86558075e-322,
...
7.10580593e+159])
(3)arange
range的numpy版,支持浮点数。
>>> np.arange(10)
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
# 设置起始值和结束值
>>> np.arange(3,9)
array([3, 4, 5, 6, 7, 8])
# 设置起始值、结束值和步长(python的range没有步长设置)
>>> np.arange(2,7,0.5) # 注意:步长可以为小数
array([2. , 2.5, 3. , 3.5, 4. , 4.5, 5. , 5.5, 6. , 6.5])(4)linespace
数学中的概念:线性空间。它与arange使用非常相似。但第三个参数不是步长还是把数组分为多少份。
>>> np.linspace(0,10,11)
array([ 0., 1., 2., 3., 4., 5., 6., 7., 8., 9., 10.])
>>> _.size
11
>>> np.linspace(0,9,20)
array([0. , 0.47368421, 0.94736842, 1.42105263, 1.89473684,
2.36842105, 2.84210526, 3.31578947, 3.78947368, 4.26315789,
4.73684211, 5.21052632, 5.68421053, 6.15789474, 6.63157895,
7.10526316, 7.57894737, 8.05263158, 8.52631579, 9. ])
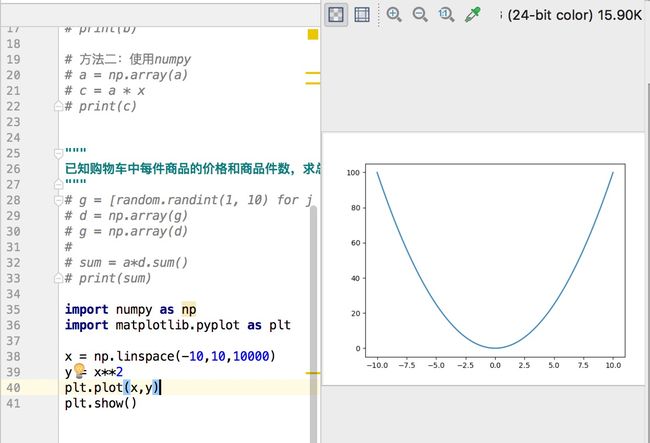
# 数学中应用
import numpy as np
import matplotlib.pyplot as plt # python的绘图库
x = np.linspace(-10,10,10000)
y = x**2
plt.plot(x,y) # 使用matplotlib来绘制点
plt.show()应用执行效果如下:
(5)eye
生成线性代数中的单位矩阵。对角线为1,其他位置是0。
>>> np.eye(5)
array([[1., 0., 0., 0., 0.],
[0., 1., 0., 0., 0.],
[0., 0., 1., 0., 0.],
[0., 0., 0., 1., 0.],
[0., 0., 0., 0., 1.]])三、ndarray-批量运算
1、数组和标量之间的运算
a+1 a*3 1//a a**0.5 a>5
>>> a = np.arange(10)
>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> a+1
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
>>> a*3
array([ 0, 3, 6, 9, 12, 15, 18, 21, 24, 27])
>>> 3/a
array([ inf, 3. , 1.5 , 1. , 0.75 ,
0.6 , 0.5 , 0.42857143, 0.375 , 0.33333333])
:1: RuntimeWarning: divide by zero encountered in true_divide 2、同样大小数组之间的运算
a+b a/b a**b a%b a==b a>b
>>> b = np.arange(10,20)
>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> b
array([10, 11, 12, 13, 14, 15, 16, 17, 18, 19])
>>> a+b
array([10, 12, 14, 16, 18, 20, 22, 24, 26, 28])
>>> a>b
array([False, False, False, False, False, False, False, False, False,
False])
>>> a[0]=20
>>> a>b
array([ True, False, False, False, False, False, False, False, False,
False])四、numPy索引和切片
ndarray对象的内容可以通过索引或切片来访问和修改,与 Python 中 list 的切片操作一样。
ndarray 数组可以基于 0 - n 的下标进行索引,切片对象可以通过内置的 slice 函数,并设置 start, stop 及 step 参数进行,从原数组中切割出一个新数组。
1、ndarray-索引
# 一维数组的索引
>>> a=np.arange(10)
>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> a[5]
5
# 多维数组的索引
>>> a = a.reshape((2,5))
>>> a
array([[0, 1, 2, 3, 4],
[5, 6, 7, 8, 9]])
# (1)列表式写法
>>> a[1][3]
8
# (2)新式写法
>>> a[1,3]
82、ndarray-切片
# 一维数组的切片
>>> a = np.arange(15)
>>> a
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14])
>>> a[0:4]
array([0, 1, 2, 3])
>>> a[:4]
array([0, 1, 2, 3])
>>> a[4:]
array([ 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14])
# 多维数组的切片
>>> a = np.arange(15).reshape((3,5))
>>> a
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]])
>>> a[0:2,0:2] # 切前两行前两列
array([[0, 1],
[5, 6]])
>>> a[1:, 2:4] # 从第二行开始切,切第3-4列
array([[ 7, 8],
[12, 13]])数组切片和列表切片的不同:数组切片时并不会自动复制(而是创建一个视图),在切片数组上的修改会影响原数组。
>>> a = np.arange(10)
>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> b = list(range(10))
>>> b
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
>>> c = a[0:4]
>>> c
array([0, 1, 2, 3])
>>> d = b[0:4]
>>> d
[0, 1, 2, 3]
>>> c[0] = 20
>>> d[0] = 20
>>> c
array([20, 1, 2, 3])
>>> d
[20, 1, 2, 3]
>>> a # 可以看到对切片数组修改影响了原数组
array([20, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> b
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]copy()方法可以创建数组的深拷贝。
>>> a[0] = 0
>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> c = a[0:4].copy()
>>> c
array([0, 1, 2, 3])
>>> c[0] = 20
>>> c
array([20, 1, 2, 3])
>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])五、高级索引
1、ndarray-布尔型索引
布尔型索引:将同样大小的布尔数组传进索引,会返回一个由所有True对应位置的元素的数组。
(1)问题:给一个数组,选出数组中所有大于5的数
# 常规方法
>>> import random
>>> a = [random.randint(0, 10) for i in range(20)]
>>> a
[8, 2, 4, 0, 9, 0, 1, 7, 10, 9, 4, 0, 5, 8, 5, 8, 4, 0, 3, 8]
>>> filter(lambda x:x>5, a)
>>> list(filter(lambda x:x>5, a))
[8, 9, 7, 10, 9, 8, 8, 8]
# 布尔索引解决
>>> a = np.array(a) # 列表转化为数组
>>> a
array([ 8, 2, 4, 0, 9, 0, 1, 7, 10, 9, 4, 0, 5, 8, 5, 8, 4,
0, 3, 8])
>>> a[a>5]
array([ 8, 9, 7, 10, 9, 8, 8, 8]) 原理:数组和标量的运算,a > 5 会对a中的每一个元素进行判断,返回一个布尔数组。
布尔型索引,将同样大小的布尔数组传进索引,会返回一个由所有True对应位置的元素的数组。
(2)问题:给一个数组,选出数组中所有大于5的偶数。
>>> a
array([ 8, 2, 4, 0, 9, 0, 1, 7, 10, 9, 4, 0, 5, 8, 5, 8, 4,
0, 3, 8])
>>> b = a[a>5]
>>> b
array([ 8, 9, 7, 10, 9, 8, 8, 8])
>>> b[b%2==0]
array([ 8, 10, 8, 8, 8])
# 合并写法
>>> a
array([ 8, 2, 4, 0, 9, 0, 1, 7, 10, 9, 4, 0, 5, 8, 5, 8, 4,
0, 3, 8])
>>> a[(a>5) & (a%2==0)] # 与运算 注意:& 和 and的区别
array([ 8, 10, 8, 8, 8])(3)问题:给一个数组,选出数组中所有大于5的数和偶数。(or)
# 或运算,or关系
a[(a>5) | (a%2==0)]
array([ 8, 2, 4, 0, 9, 0, 7, 10, 9, 4, 0, 8, 8, 4, 0, 8])2、ndarray-花式索引
花式索引指的是利用整数数组进行索引。
花式索引根据索引数组的值作为目标数组的某个轴的下标来取值。对于使用一维整型数组作为索引,如果目标是一维数组,那么索引的结果就是对应位置的元素;如果目标是二维数组,那么就是对应下标的行。
花式索引跟切片不一样,它总是将数据复制到新数组中。
(1)问题:对于一个数组,选出其第1,3,4,6,7个元素,组成新的二维数组。
>>> a = np.arange(20)
>>> a
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19])
>>> a[[1,3,4,6,7]] # 整数数组索引
array([1, 3, 4, 6, 7])(2)问题:对一个二维数组,选出其第一列和第三列,组成新的二维数组。
>>> a = np.arange(20).reshape(4,5)
>>> a
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]])
>>> a[0, 2:4]
array([2, 3])
>>> a[0]>2
array([False, False, False, True, True])
>>> a[0, a[0]>2]
array([3, 4])
# 注意花式索引不能同时出现在逗号两边,比如想选择6、8、16、18
>>> a[[1,3], [1,3]]
array([ 6, 18]) # 实际取的是a[1,1] 和a[3,3]的值
# 实际解法如下所示:
>>> a[[1,3],:] # 第1行到第4行,列全切
array([[ 5, 6, 7, 8, 9],
[15, 16, 17, 18, 19]])
>>> a[:,[1,3]] # 行全切,切第一列到第三列
array([[ 1, 3],
[ 6, 8],
[11, 13],
[16, 18]])
>>> a[[1,3],:][:,[1,3]]
array([[ 6, 8],
[16, 18]])六、NumPy-array通用函数
通用函数:能同时对数组中所有元素进行运算的函数。常见通用函数如下所示:
1、一元函数
abs,sqrt,exp,log,ceil,floor,rint,trunc,modf,isnan,isinf,cos,sin,tan
>>> a = np.arange(-5,5)
>>> a
array([-5, -4, -3, -2, -1, 0, 1, 2, 3, 4])
>>> np.abs(a) # 取绝对值
array([5, 4, 3, 2, 1, 0, 1, 2, 3, 4])
>>> abs(a)
array([5, 4, 3, 2, 1, 0, 1, 2, 3, 4])
>>> np.sqrt(a) # 开方
:1: RuntimeWarning: invalid value encountered in sqrt
array([ nan, nan, nan, nan, nan,
0. , 1. , 1.41421356, 1.73205081, 2. ])
# 向下取整:单个是math.floor();批量是:np.floor()
>>> import math
>>> math.floor(-1.6)
-2
>>> math.floor(1.6)
1
# 向上取整:单个是math.ceil(),批量是np.ceil()
>>> math.ceil(1.6)
2
>>> math.ceil(-1.6)
-1
# 四舍五入:round()
>>> round(1.6)
2
>>> round(-1.6)
-2
>>> round(-1.3)
-1
# 批量操作
>>> a = np.arange(-5.5, 5.5)
>>> a
array([-5.5, -4.5, -3.5, -2.5, -1.5, -0.5, 0.5, 1.5, 2.5, 3.5, 4.5])
>>> np.floor(a) # 向下取整
array([-6., -5., -4., -3., -2., -1., 0., 1., 2., 3., 4.])
>>> np.ceil(a) # 向上取整
array([-5., -4., -3., -2., -1., -0., 1., 2., 3., 4., 5.])
>>> np.round(a) # 四舍五入
array([-6., -4., -4., -2., -2., -0., 0., 2., 2., 4., 4.])
>>> np.rint(a) # 四舍五入(同round())
array([-6., -4., -4., -2., -2., -0., 0., 2., 2., 4., 4.])
>>> np.trunc(a) # 截断(丢弃小数部分)
array([-5., -4., -3., -2., -1., -0., 0., 1., 2., 3., 4.])
# modf:整数和小数部分分拆
>>> a
array([-5.5, -4.5, -3.5, -2.5, -1.5, -0.5, 0.5, 1.5, 2.5, 3.5, 4.5])
>>> np.modf(a)
(array([-0.5, -0.5, -0.5, -0.5, -0.5, -0.5, 0.5, 0.5, 0.5, 0.5, 0.5]), array([-5., -4., -3., -2., -1., -0., 0., 1., 2., 3., 4.]))
>>> k,y = np.modf(a)
>>> k
array([-0.5, -0.5, -0.5, -0.5, -0.5, -0.5, 0.5, 0.5, 0.5, 0.5, 0.5])
>>> y
array([-5., -4., -3., -2., -1., -0., 0., 1., 2., 3., 4.]) 2、二元函数
add,substract,multiply,divide,power,mod,maximum,mininum
# maximum:对两个数组每个值均取最大值
>>> a
array([3, 4, 5, 6, 7])
>>> b
array([3, 0, 5, 0, 7])
>>> np.maximum(a,b)
array([3, 4, 5, 6, 7])
# minimum:对两个数组每个值均取最小值
>>> np.minimum(a,b)
array([3, 0, 5, 0, 7])3、补充:浮点数特殊值
Numpy中创建特殊值:np.nan np.inf
在数据分析中,nan常被用作表示数据缺失值。
# python中有两个浮点数特殊值
>>> float('3.5')
3.5
>>> float('nan')
nan
>>> float('inf')
inf
# nan(Not a Number):不等于任何浮点数(nan != nan)
>>> a = np.arange(5)
>>> a
array([0, 1, 2, 3, 4])
>>> a/a
:1: RuntimeWarning: invalid value encountered in true_divide
array([nan, 1., 1., 1., 1.])
>>> np.nan # 获取nan值
nan
>>> np.nan == np.nan # 两个nan不相等,因为nan不等于任何值
False
>>> b = a/a
>>> b
array([nan, 1., 1., 1., 1.])
>>> np.isnan(b) # 判断出数组中哪些是nan值
array([ True, False, False, False, False])
>>> b[~(np.isnan(b))] # ~取反
array([1., 1., 1., 1.])
# inf(infinity):比任何浮点数都大,表示无穷大的数
>>> float('inf') > 10000000
True
>>> a = np.array([3,4,5,6,7])
>>> b = np.array([3,0,5,0,7])
>>> a/b
array([ 1., inf, 1., inf, 1.])
>>> np.inf == np.inf # 无穷大的数可以相等
True
# 过滤掉数组中inf的数
>>> c = a/b
>>> c
array([ 1., inf, 1., inf, 1.])
>>> c[c!=np.inf]
array([1., 1., 1.])
# 利用isinf()的写法
>>> c[~np.isinf(c)]
array([1., 1., 1.]) 七、NumPy-数学和统计方法
>>> a
array([3, 4, 5, 6, 7])
# sum:求和
>>> a.sum()
25
# mean:求平均数
>>> a.mean()
5.0
# var:求方差,方差表示整组数据的离散程度
>>> a.var()
2.0
# 方差公式验证:
>>> a
array([3, 4, 5, 6, 7])
>>> ((3-5)**2 + (4-5)**2 + (5-5)**2 + (6-5)**2 + (7-5)**2)/5
2.0
# std:求标准差(对方差开根)
>>> a.std()
1.4142135623730951
>>> math.sqrt(2)
1.4142135623730951
# 标准差和均值可以估计整个数组的范围
>>> a = np.arange(0,10,0.2)
>>> a
array([0. , 0.2, 0.4, 0.6, 0.8, 1. , 1.2, 1.4, 1.6, 1.8, 2. , 2.2, 2.4,
2.6, 2.8, 3. , 3.2, 3.4, 3.6, 3.8, 4. , 4.2, 4.4, 4.6, 4.8, 5. ,
5.2, 5.4, 5.6, 5.8, 6. , 6.2, 6.4, 6.6, 6.8, 7. , 7.2, 7.4, 7.6,
7.8, 8. , 8.2, 8.4, 8.6, 8.8, 9. , 9.2, 9.4, 9.6, 9.8])
>>> a.mean()
4.9
>>> a.std() # 标准差
2.8861739379323628
>>> a.mean()-a.std() # 大概估计数组的范围
2.0138260620676376
>>> a.mean()-2*a.std()
-0.8723478758647252
>>> a.mean()+2*a.std()
10.672347875864727
# min:求最小值
>>> a.min()
0.0
# max:求最大值
>>> a.max()
9.8
# argmin:求最小值索引
>>> a.argmin()
0
# argmax:求最大值索引
>>> a.argmax()
49八、NumPy-随机数生成
# python默认的random模块
>>> random.random()
0.5107400270751336
>>> random.randint(0,10)
9
>>> random.choice([1,3,4,5])
5
# shuffle():用于将列表中元素打乱
>>> a = [1,3,4,5,7]
>>> random.shuffle(a) # 打乱列表
>>> a
[1, 4, 7, 3, 5]
# uniform(a,b):用于生成一个指定范围内的整数。其中参数a是下限,参数b是上限,生成的随机数n:a<=n<=b
>>> random.uniform(2.0,4.0)
2.190653911434251
# 随机函数在np.random子包内方法
# rand:给定形状产生随机数组(0到1之间的数)
>>> np.random.rand(10)
array([0.28624648, 0.69121364, 0.74607992, 0.2587513 , 0.60445688,
0.2890542 , 0.88712216, 0.93544304, 0.99640741, 0.73059636])
# randint:给定形状产生随机整数
>>> np.random.randint(0,10) # 取范围内随机数
3
>>> np.random.randint(0,10,10) # 用随机数生成一个有10个元素的数组
array([7, 5, 6, 8, 5, 4, 1, 9, 7, 4])
>>> np.random.randint(0,10,(3,5)) # 用随机数生成一个三行五列的二维数组
array([[2, 1, 5, 0, 9],
[5, 4, 8, 7, 3],
[2, 0, 5, 9, 9]])
>>> np.random.randint(0,10,(3,5,5)) # 用随机数生成一个三维数组
array([[[7, 4, 8, 5, 9],
[8, 1, 4, 3, 5],
[9, 8, 9, 3, 1],
[8, 8, 7, 0, 7],
[7, 0, 8, 6, 8]],
[[3, 1, 8, 1, 2],
[8, 2, 7, 6, 4],
[4, 3, 8, 0, 6],
[3, 5, 3, 1, 2],
[4, 2, 6, 6, 2]],
[[4, 5, 5, 4, 6],
[0, 7, 5, 6, 6],
[6, 4, 8, 8, 2],
[5, 0, 3, 7, 9],
[8, 5, 6, 2, 5]]])
# choice:给定形状产生随机选择
>>> np.random.choice([1,2,3,4,5])
2
>>> np.random.choice([1,2,3,4,5],10)
array([1, 2, 1, 4, 1, 3, 2, 5, 3, 2])
# shuffle:与random.shuffle相同
# uniform:给定形状产生随机数组
>>> np.random.uniform(2.0,5.0)
2.9530512208056257
>>> np.random.uniform(2.0,5.0,10)
array([3.9142783 , 4.71991751, 4.05954663, 4.13170221, 3.88043716,
2.00233882, 2.34833856, 2.48430517, 3.07240671, 3.4608536 ])