树结构整理(python)

本博客来自于对左神初级班的笔记整理

1、实现二叉树先序、中序、后序排列，使用递归和非递归的方式

（1）先序

        非递归方式用栈来实现，弹出结点时，有右先压右，然后压左。题目地址：https://leetcode-cn.com/problems/binary-tree-preorder-traversal/

# 先序遍历
class TreeNode(object):
    def __init__(self, x=0, left=None, right=None):
        self.val = x
        self.left = left
        self.right = right
class Solution(object):
    def __init__(self, root=0):
        self.root = root
    # 递归方式
    def preorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        if root == None:
            return []
        l = []
        l.append(root.val)
        l += self.preorderTraversal(root.left)
        l += self.preorderTraversal(root.right)
        return l
    # 非递归方式
    def preorderTraversal2(self, root):
        if root == None:
            return []
        stack = []
        l = []
        stack.append(root)
        while stack:
            root = stack.pop()
            l.append(root.val)
            if root.right:
                stack.append(root.right)
            if root.left:
                stack.append(root.left)
        return l
if __name__ == '__main__':
    n4 = TreeNode(4)
    n5 = TreeNode(5)
    n6 = TreeNode(6)
    n7 = TreeNode(7)
    n2 = TreeNode(2, n4, n5)
    n3 = TreeNode(3, n6, n7)
    n1 = TreeNode(1, n2, n3)
    bt = Solution(n1)
    print(bt.preorderTraversal2(n1))

（2）中序

        题目地址：https://leetcode-cn.com/problems/binary-tree-inorder-traversal/

        非递归方式是先申请一个栈，将所有左边界压入栈，直至cur=null，将结点弹出，并让cur=cur.right，继续重复。原理是可以按照左边界依次划分，就可以完美遍历。图示如下：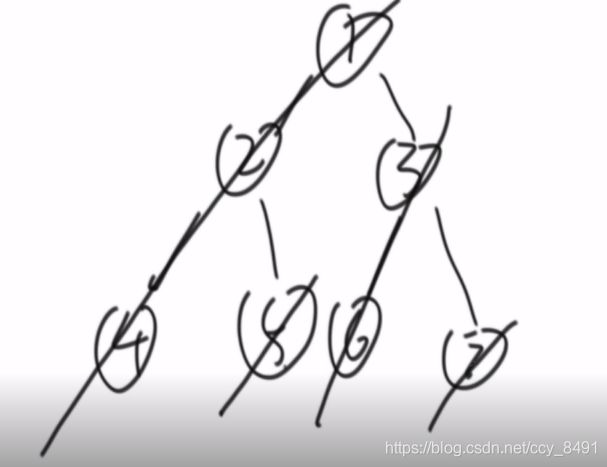

 

 

    # 中序递归
    def inorderTraversal(self, root):
        if root == None:
            return []
        l = []
        l += self.inorderTraversal(root.left)
        l.append(root.val)
        l += self.inorderTraversal(root.right)
        return l
    # 中序非递归
    def inorderTraversal2(self, root):
        if root == None:
            return []
        stack = []
        l = []
        while stack or root:
            if root:
                stack.append(root)
                root = root.left
            else:
                root = stack.pop()
                l.append(root.val)
                root = root.right
        return l

（3）后序

        简单非递归想法是用两个栈，一个用于将结点压入栈中，记为s1，一个用于存储弹出结点的值，记为s2。每棵子树的头结点先从s1中弹出，然后将该结点的孩子结点按照先左再右的顺序压入s1，那么从s1弹出的顺序就是先右再左，所以s1中弹出的顺序就是中右左，再通过s2实现左右中。

    # 后序递归
    def postorderTraversal(self, root):
        if root == None:
            return []
        l = []
        l += self.postorderTraversal(root.left)
        l += self.postorderTraversal(root.right)
        l.append(root.val)
        return l
    # 后序非递归
    def postorderTraversal2(self, root):
        if root == None:
            return []
        stack1 = []
        stack2 = []
        stack1.append(root)
        while stack1:
            root = stack1.pop()
            stack2.append(root.val)
            if root.left:
                stack1.append(root.left)
            if root.right:
                stack1.append(root.right)
        # 这里按道理讲是将stack2按照栈的方式弹出，但是python中的栈也是列表
        return stack2[::-1]

2、找到一棵二叉树的后继（前驱）结点

        假设二叉树中多了parent指针。假设有一 棵Node类型的节点组成的二叉树，树中每个节点的parent指针都正确地指向自己的父节点，头节点的parent指向null。只给一个在二叉树中的某个节点 node，请实现返回node的后继节点的函数。在二叉树的中序遍历的序列中， node的下一个结点叫作node的后继节点，上一个结点叫做前驱结点。

        主要思想参见博客https://blog.csdn.net/zxzxzx0119/article/details/81097546，此处不再复述

 

3、二叉树序列化、反序列化

        序列化是将一个数据结构或者对象转换为连续的比特位的操作，进而可以将转换后的数据存储在一个文件或者内存中，同时也可以通过网络传输到另一个计算机环境，采取相反方式重构得到原数据。题目来源https://leetcode-cn.com/problems/serialize-and-deserialize-binary-tree/

        此处用前序遍历表示：

    # 序列化
    def serialize(self, root):
        if root == None:
            return "#!"
        l = ''
        l += str(root.val) + '!'
        l += self.serialize(root.left)
        l += self.serialize(root.right)
        return l
    # 反序列化
    def deserialize(self, data):
        values = data.split('!')
        return self.deserialize_pre_str(values)
    def deserialize_pre_str(self,values):
        value = values.pop(0)
        if value == '*':
            return None
        root = TreeNode(value)
        root.left = self.deserialize_pre_str(values)
        root.right = self.deserialize_pre_str(values)
        return root

4、判断一棵树是否为平衡二叉树

        平衡二叉树的定义为左右子树高度差不超过1.此处用递归非常好解。主要思想为考察每个为头结点的树是否平衡。可分为三步：（1）考察左子树是否平衡（2）考察右子树是否平衡（3）考察左右子树高度差是否不超过1.总体来说，可以将求二叉树的最大深度加上一个判别左右子树高度差即可。题目地址：https://leetcode-cn.com/problems/balanced-binary-tree/

    # 求是否为平衡二叉树
    def isBalanced(self, root):
        if not root:
            return True
        if abs(self.getDepth(root.left) - self.getDepth(root.right)) >1:
            return False
        return self.isBalanced(root.left) and self.isBalanced(root.right)
    def getDepth(self,root):
        if not root:
            return 0
        return max(self.getDepth(root.left)+1, self.getDepth(root.right)+1)

5、判断一棵树是否为搜索二叉树

        二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树（来源于百度百科）。题目地址：https://leetcode-cn.com/problems/validate-binary-search-tree/

        判断的方法为中序遍历后，看遍历后是否为升序即可。采用非递归中序为基础框架：

def isValidBST(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        if root == None:
            return True
        stack = []
        pre = -0xfffff
        # 这里加入一个flag标志是因为案例中有[-2147483647]这个，如果不加会报错
        flag = 0
        while stack or root:
            if root:
                stack.append(root)
                root = root.left
            else:
                root = stack.pop()
                cur = root.val
                if cur <= pre and flag != 0:
                    return False
                else:
                    pre = cur
                    flag = 1
                root = root.right
        return True

6、判断一棵树是否为完全二叉树

        完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。

        判断方式：采用层序遍历，如果当前结点有右子树无左子树，则return False；如果只有左子树，则后面遇到的结点必都为叶结点。

    def isValidCBT(self,root):
        if not root:
            return True
        queue = [root]
        # 此处设置一个变量表示是否要开启以后都为叶结点的状态
        leaf = False
        while queue:
            if (leaf and (root.left != None or root.right != None)) or (root.left == None and root.right != None):
                return False
            root = queue.pop(0)
            if root.left:
                queue.append(root.left)
            if root.right:
                queue.append(root.right)
            else:
                leaf = True
        return True

7、已知一棵完全二叉树，求其结点的个数

要求：时间复杂度低于O(N)，N为这棵树的节点个数

        根据结论满二叉树的结点个数为来加速。首先先记录最左边界的深度，即为最后一层，再遍历右子树左边界是否到了最后一层，到了就证明这棵树的左子树是满的，左子树即可求结点数，再递归去求右子树的结点个数。如果右子树左边界没到最后一层，则右子树就是满的，只不过高度比左子树减一。

    # 求完全二叉树的结点个数
    def countNodes(self, root):
        if not root:
            return 0
        return self.bs(root, 1, self.mostlevel(root, 1))
    def bs(self, root, level, height):
        if level == height:
            return 1
        # 右子树的左边界高度等于整棵树的高度，返回左子树的结点个数加上右子树递归,height为树的总体高度，level为当前高度
        if self.mostlevel(root.right,level+1) == height:
            return 2**(height-level) + self.bs(root.right, level+1, height)
        # 否则返回右子树的节点个数加上左子树递归
        else:
            return 2**(height-level-1) + self.bs(root.left, level+1, height)
    # mostlevel用来求数的左边界深度
    def mostlevel(self, root, level):
        while root:
            level += 1
            root = root.left
        return level - 1