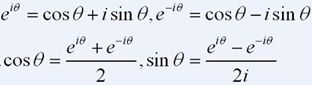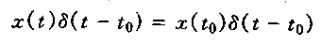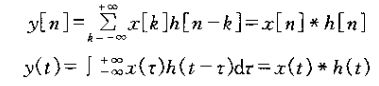傅里叶变换回顾与总结

傅里叶变换回顾与总结
对傅里叶变换进行回顾总结，遗忘，要用的时候回顾此浓缩版即可。内容来源于不同出处，函数名称、符号使用不是十分统一，一维二维表达同时存在，略表歉意。

1，两个前提
线性性

两个信号加权和输出为它们分别输出和的加权，权值为标量。

时不变性

 

2，两个信号
复指数信号及其性质

欧拉公式

 

冲激函数及其性质

 

3，运行线性性，将原信号表示为冲激函数的加权和（积分）

 

4，冲激响应函数（脉冲响应函数，点扩散函数）：系统对冲激函数的输出
h(t)=O[δ(t)]
运用时不变特性
h(t-τ)=O[δ(t-τ)]
5，卷积的由来
再次运用叠加原理，由于信号x(t)为冲击信号的加权和，那么系统对x(t)的输出g(t)则为系统对这些冲击信号输出的加权和。注意x(τ)是函数值，相当于权重。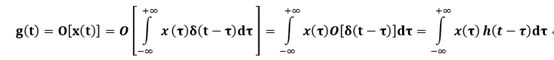

表示为g(t)=x(t)*h(t)

 

卷积的傅里叶变换，傅里叶变换的一些性质

等等

傅里叶变换的本质

 

变换是去分解，由于线性性，因此可以把原函数表示成一组正交基函数的加权和。正交性是任意两个不同基函数乘积后的积分为0，相同则为1。傅里叶变换的基函数是复指数信号，两个不同频率的复指数信号乘积积分和为0. 而同频率复指数信号积分和为1.

傅里叶变换：求取不同频率复指数信号的权重
为什么傅里叶变换要这么计算？
信号=不同频率的复指数信号加权和。
将信号乘积某一个频率的复指数信号然后积分，这样，同频率复指数信号与它相乘积分后留下权重，而不通过频率复指数信号与它相乘积分后只剩下0。最终得到了该频率复指数信号的权重。
傅里叶反变换：将原信号表示为权重乘以不同频率复指数信号的叠加（积分）。
知道这个本质，有些信号直接看原函数就能知道傅里叶变换是什么样，例如正弦余弦函数，经过欧拉公式，它们已经是两个复指数信号的加权和了。

 

参考资料
1，信号与系统，奥本海默，第二版
2，2-D Fourier Transforms, Yao Wang, Polytechnic University Brooklyn NY 11201 , Brooklyn, NY 11201
3，Diffraction, Fourier Optics and Imaging, OKAN K. ERSOY

 

LuchangLi

HUST

20170818

转载于:https://www.cnblogs.com/luchangli/p/7396009.html