概率模型（四）：条件随机场(CRF)

条件随机场(Conditional Random Field,CRF)是一个比较重要的概率模型，在详细介绍CRF之前，首先简单介绍一下概率图(Probabilistic Graphical Model,PGM)，有时候简称图模型(Graphical Model, GM).

PGM

概率图模型用图的形式表示一组随机变量。图中的节点表示一个或一组随机变量，图中的边代表随机变量间的依赖关系。

概率图模型分为有向图模型和无向图模型，如下：

下面将依次介绍

有向图模型

有向图模型中，我们主要考虑贝叶斯网络，它满足下面特征的模型：

对于一个无向图$G$以及它表示的一组随机变量$X=x_1,x_2,...,x_N$,$x_i$的所有父节点组成的集合我们记作$X_{\pi i}$,如果$X$的联合概率分布可以表示为：

$$p(X)=\prod _{i=1}^{N}p(x_i|x_{\pi i})$$

那么$G$被称为一个贝叶斯网络

常见的贝叶斯网络有：sigmoid信念网络（SBN），朴素贝叶斯模型，以及上篇的隐马尔科夫模型。

SBN

模型的局部条件概率表示为：

$$p(x_k|X_{\pi k},W)=\sigma (w_0+\sum _{x_i\in X_{\pi k}}{w}_i{x}_i)$$

朴素贝叶斯

模型的局部条件表示为：

$$P(x_k|X_{\pi k})=\frac{P(X_{\pi k}|x_k)P(x_k)}{P(X_{\pi k})}$$

$$\propto P(X_{\pi k}|x_k)P(x_k)$$
$$=P(x_k)\prod _{x_i\in X_{\pi k}}P(x_i|x_k)$$

隐马尔科夫模型

上一篇详细介绍了此模型，它的联合分布概率表示为：
$$P(Q,V)=\prod _{q_t\in Q,v_t\in V}P(v_t|v_{t-1})P(q_t|v_t)$$

其中$P(v_t|v_{t-1})$是转移概率，$P(q_t|v_t)$为输出概率。

无向图模型

对于无向图模型，我们主要考虑马尔科夫随机场(Markov Random Field,MRF),也称为马尔科夫网络(Markov Network).

无向图G,图中的节点表示随机变量，边表示随机变量间的依赖关系。如果图中随机变量的联合概率分布P(X)满足成对、局部或全局马尔可夫性，则G被称为马尔科夫随机场

那么我们分别来解释下成对、局部、全局马尔科夫性分别是什么性质。

成对马尔科夫性

无向图中的任意不直接相连的两个节点$x_i,x_j$，以及除它们之外的所有节点组成的集合,记作$X_O$.

如果给定$X_O$的情况下，$x_i,x_j$条件独立，则称无向图满足成对马尔科夫性质,即：

$$P(x_i,x_j|X_O)=P(x_i|X_O)P(x_j|X_O)$$

局部马尔科夫性

无向图中的任意一个节点$x_k$, 与之直接向量的节点组成的集合，记作$X_{N(k)}$,$x_k$之外的所以其他节点组成的集合，记作$X_{-k}$.

如果：

$$P(x_k|X_{N(k)})=P(x_k|X_{-k})$$

则称无向图满足局部马尔科夫性。

全局马尔科夫性

无向图中不直接相邻节点集合$X_A,X_B$,已经连接他们的节点组成的集合$X_C$。

如果:

$$P(X_A,X_B|X_C)=P(X_A|X_C)P(X_B|X_C)$$

则称无向图满足全局马尔科夫性。

有向图中联合概率分布可以分解为局部条件概率的乘积形式，无向图中的联合概率分布如果计算呢？

无向图中的边不表示因果依赖关系，所以不能运用链式法则分解为条件概率的乘积形式。在介绍无向图联合概率分解方法之前，先引入团的概念。

无向图中的全联通子图，有称为团，如果一个团加入任何一个节点后不能构成团，则称之为最大团

HC定理

无向图满足成对、局部或全局马尔科夫性，当且仅当联合分布概率可以表示一系列定义在最大团上的非负函数的乘积形式，即：

$$P(X)=\frac{1}{Z}\prod _{X_c\in C}\varphi (X_c)$$
其中，
$$Z=\sum _{X_c\in C}\varphi (X_c)$$

称为配平函数(partition function),$\varphi (X_c)\ge 0$称为势能函数，$X_c$为一个最大团，$C$为最大团组成的集合。

由于势能函数必须是非负的，所以经常采用势能函数：

$$\varphi (X_c)=exp(-E(X_c))$$

其中$E(X_c)$被称为能量函数。如此，联合概率分布可表示为：

$$P(X)=\frac{1}{Z}\prod _{X_c\in C}\varphi (X_c)$$
$$=\frac{1}{Z}\prod _{X_c\in C}exp(-E(X_c))$$
$$=\frac{1}{Z}exp(\sum _{X_c\in C}-E(X_C))$$

条件随机场就是常见的无向图模型之一，另外常见的无向图模型还有对数线性模型、玻尔兹曼机和受限玻尔兹曼机。介绍条件随机场之前，先简单介绍一下对数线性模型，玻尔兹曼机与受限玻尔兹曼机在之前的文章里已有介绍，不再赘述。

对数线性模型

势能函数采用：
$${\varphi }_c(X_c|{\theta }_c)=exp({\theta }_c^T{f}_c(X_c))$$

所以联合分布概率表示为：

$$P(X|\theta )=\frac{1}{z(\theta )}\prod _{X_c\in C}exp({\theta }_C^T{f}_c(X_c))$$

$$log(P(X|\theta ))=log(\prod _{X_c\in C}exp({\theta }_c^T{f}_c(X_c)))-log(z(\theta ))$$
$$=\sum _{x_c\in C}{\theta }_c^T{f}_c(X_c)-log(z(\theta ))$$

$$P(X|\theta )=exp(\sum _{x_c\in C}{\theta }_c^T{f}_c(X_c)-log(z(\theta )))$$
$$=\frac{1}{z(\theta )}exp(\sum _{x_c\in C}{\theta }_c^T{f}_c(X_c))$$

如果采用对数线性模型建模条件概率，因为在给定一组随机变量$X$的情况下，此时是无向图中只有一个节点$y$,它的最大团只有一个，也就是$\{y\}$,因此得出：

$$P(y|X,\theta )=\frac{1}{Z(\theta )}exp({\theta }^{T}f(X,y))$$

有了以上的这些基础知识，理解条件随机场模型就很简单了

条件随机场模型(Conditional Random Field)

条件随机场（Conditional Random Field， CRF）也是一种无向图模型。它是在给定随机变量X的条件下，随机变量Y的马尔科夫随机场,因此由HC定量得出：

$$P(Y|X,\theta )=\frac{1}{Z(X,\theta )}\prod _{Y_c\in C}\varphi (X,Y_c)$$

当我的势能函数采用：
$${\varphi }_c(X_c|{\theta }_c)=exp({\theta }_c^T{f}_c(X_c))$$

得出：

$$P(Y|X,\theta )=\frac{1}{z(X,\theta )}exp(\sum _{Y_c\in C}{\theta }^{T}f(X,Y_c))$$

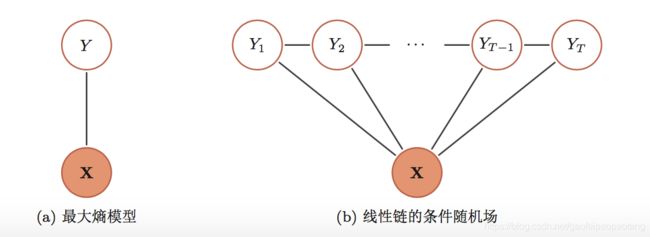
可以看出，它是对数线性模型的一种扩展，下图对比了对数线性模型，也成为最大上模型和条件随机场：

上图展示的是比较常见的链式条件随机场，它的最大团为$\{Y_1,Y_2\},\{Y_2,Y_3\},...\{Y_t,Y_{t+1}\},...\{Y_{T-1},Y_T\}$, 因此它的概率分布表示为：

$$P(Y|X,\theta )=\frac{1}{Z(X,\theta )}exp(\sum _{t=1}^{T-1}{\theta }^{T}f(X,Y_t,Y_{t+1}))$$

一般来说，我们的特征函数$f$一般取两方面的特征，也就是$Y_t$的位置相关的特征$f_1$,以及上线文特征$f_2$,因此概率分布表示为：

$$P(Y|X,\theta )=\frac{1}{z(X,\theta )}exp(\sum _{t=1}^T{\theta }_1^{T}f(X,Y_t)+\sum _{t=1}^{T-1}{\theta }_2^{T}f(X,Y_t,Y_{t+1}))$$

相关算法

图模型模型相关的问题分为两大类，也就是推断问题和学习问题。

推断问题指的是已知部分变量情况下，计算其他变量的后验概率分布的问题。

学习问题是指给定一定的观察数据，学习图模型的结构和参数的问题。

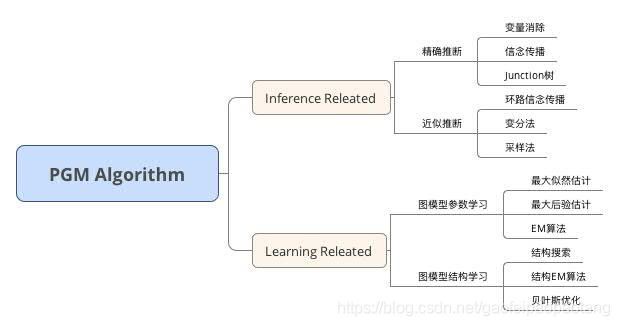
领域内的算法简单总结如下：