深度篇—— CNN 卷积神经网络(一) 细说 cnn 卷积神经网络
返回主目录
返回 CNN 卷积神经网络目录
下一章：深度篇—— CNN 卷积神经网络(二) 细说 池化(pooling) 与 反池化(unpooling)
目录内容
深度篇—— CNN 卷积神经网络(一) 细说 cnn 卷积神经网络
深度篇—— CNN 卷积神经网络(二) 细说 池化(pooling) 与 反池化(unpooling)
深度篇—— CNN 卷积神经网络(三) 关于 ROI pooling 和 ROI Align 与 插值
深度篇—— CNN 卷积神经网络(四) 使用 tf cnn 进行 mnist 手写数字 代码演示项目
本小节，细说 CNN 卷积神经网络，下一小节细说 池化 与 反池化
一. CNN 卷积神经网络
1. CNN 卷积神经的理解
CNN 卷积神经网络 (Convolution Neural Network, CNN) 是一种前馈神经网络，它的人工神经元可以响应一部分覆盖范围内的周围单元 ，对于大型图像处理有出色表现。卷积神经网络由一个或多个卷积层和顶端的全连接层组成，同时也包括关联权重和池化层。
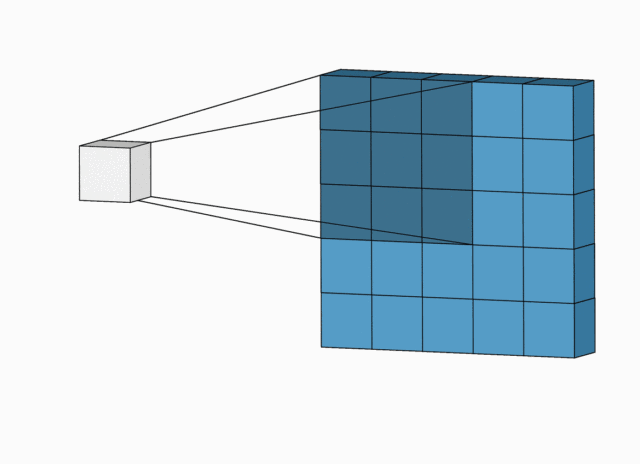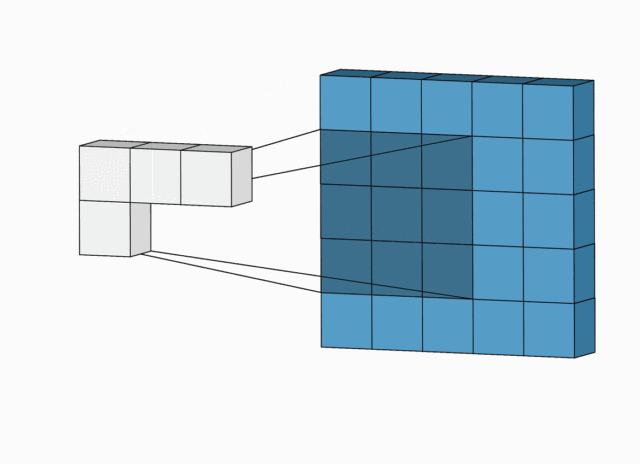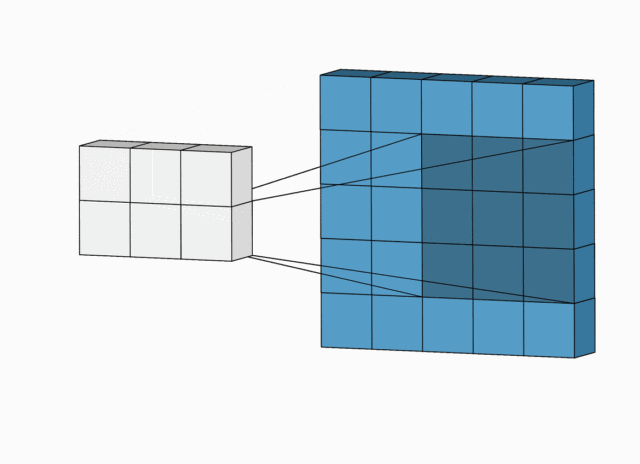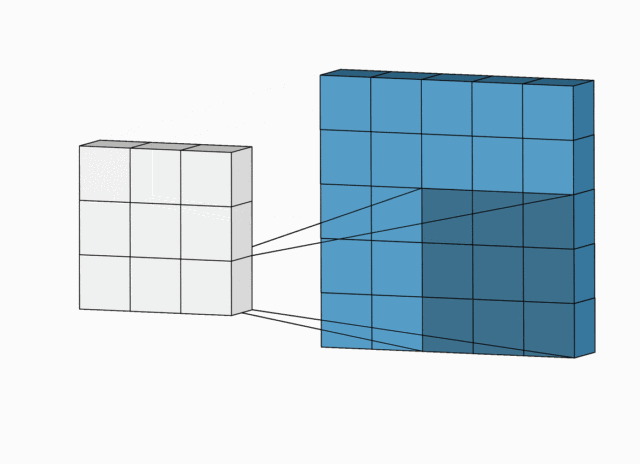
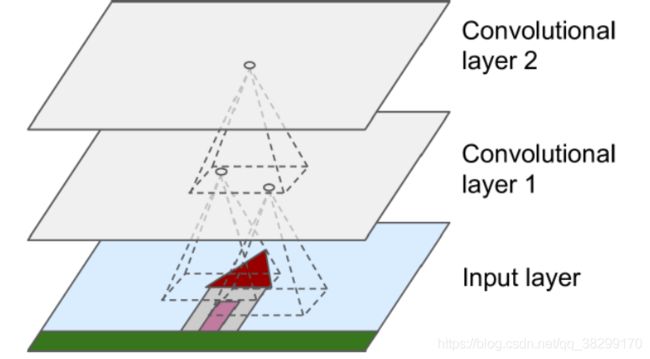
卷积神经，是依靠感受野(也就是滑动窗口)去提取特征进行学习 的。
滑动窗口，就好像上图的圆圈一样，从 1 的位置，滑动到 2 的位置，再滑动到 3 的位置。滑动完一行之后，再移动都下一行去 滑动，然后，又滑动到 m 位置，再滑动到 n 的位置。这滑动窗口，就好像人的扫视一样。滑动窗口的大小，称为感受野，也就是一次能感受到多少信息量。
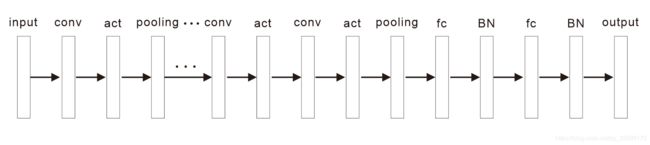
2. CNN 的层级结构
(1). CNN 依旧是层级网络
(2). CNN层级的形式(运算) 与功能做了变化
(3). 主要是以下层级
①. 数据输入层 (input layer)
②. 卷积计算层 (convolution layer)
③. 激励函数层 (activation layer)
④. 池化层 (pooling layer)
⑤. 全连接层 (full connected layer)
⑥. BN 层 (Batch Normalization layer)
⑦. 输出层 (output layer)
(4). 层级一般依次：
![[(Conv \rightarrow act) \times m \rightarrow pooling(?)] \times n \rightarrow (fc \rightarrow act) \times k \rightarrow output](http://img.e-com-net.com/image/info8/3e4db56fb61943219f3a26c03a650412.gif){kind=small}
3. CNN 卷积层 (convolution layer)
(1). 卷积层是由多个特征面 (feature map) 组成的，每个特征面由多个神经元组成，它的每一个神经元通过卷积核(filter) 与上一层特征面的局部区域相连。
(2). 卷积核 (filter) 是一个权值矩阵。(如对于二维而言，可为 
或 
的矩阵)
在二维卷积函数 tf.nn.conv2d() 中会有参数 filter。
filter = [filter_height, filter_width, in_channels, out_channels]
filter_height：为卷积核的高
filter_width：为卷积核的宽
in_channels：为输入的通道数
out_channels：为输出的通道数，即为当前卷积层的卷积核个数。
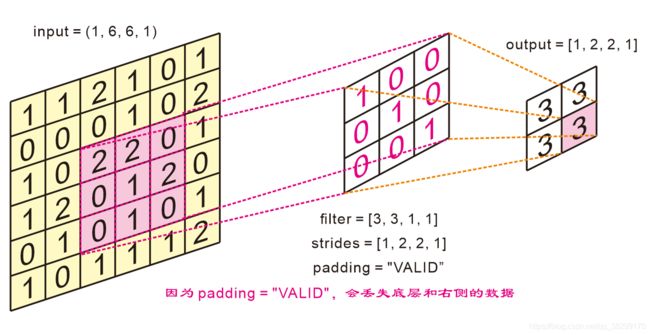
(3). 卷积核滑动的步幅(stride，也称步长) 即卷积核每一次平移的距离；和 填充 (padding) 模式 即使用卷积时图像某部分做运算时，可能会有部分没有覆盖到(如边界)，需要决定是否填充以及使用什么填充方式，是卷积层的两个重要参数。
①. 在二维卷积函数 tf.nn.conv2d()，最大池化函数 tf.nn.max_pool()，平均池化函数 tf.nn.avg_pool() 中会有参数 strides 和 padding。
②. strides = [b, h, w, c]
b：为样本上的步长，默认为 1，也就是每个样本都会进行运算。
h：为 filter 在高度上移动的步长，默认为 1，这个值可以自己设定，根据网络的结构合理调节。
w：为 filter 在宽度上移动的步长，默认为 1，这个值可以自己设定，根据网络的结构合理调节。
c：为在通道上移动的步长，默认值为 1，这个表示每一个通道都会进行移动和运算。
③. padding 模式
a. padding = "SAME"
设置为 SAME 时，则卷积层在必要的时候使用零填充(默认为使用 零 填充，也有其他值填充方式)。在这种情况下，输出神经元数量等于输入神经元的数量除以步幅，结果向上取整 (如 13 / 5 = 3)。然后，在输入周围尽可能均匀地填充 零。(zero-padding：零 填充)
b. padding = "VALID"
设置为 VALID，卷积层就不使用填充，根据步幅可能会忽略输入图片中位于底部和右侧的一些 行 和 列 的数据。
(4). 卷积的计算方式为内积和，即对应格子的数先相乘，再相加。
zero-padding 并不是说，一定只填充 一圈 0，而是，根据卷积核的大小，和步幅 相关 来决定的。填充两圈、三圈 0 都是有可能的，看具体情况再确定。
同样的，除了 零填充，还有 镜像填充、常数填充、重复填充 等等。
滑动窗口，都是从左上角开始，然后，向右 和 向下 进行操作的。
(5). 卷积核的理解
①. 卷积运算后，输出图像尺寸缩小(
卷积核除外)
②. 越是边缘的像素点，对输出的影响越小，因为卷积运算在移动到边缘的时候就结束了。中间的像素有可能会参与多次运算，但是，边缘像素点可能只参与一次计算。所以，结果可能会丢失边缘信息。
③. 卷积层通过卷积操作提取输入的不同特征，第一层卷积提取低级特征(如 边缘、线条、角落等)，更高层的卷积层提取更高级的特征。即：CNN 饿前几层是做边缘检测效果，后面的层有可能检测到物体的部分区域，更靠后的一些层可能检测 到完整的物体。
④. padding 的用途
a. padding = "SAME" 可保持边界信息。否则的话，输入图像最边缘的像素点信息只会被卷积核操作一次，但是图像中间的像素点会被扫描到很多次，那就会在一定程度上降低了边界信息的参考程度。但是在加入了 padding = "SAME" 之后，在实际处理过程中就会从新的边界 进行操作，从而在一定程度上解决了这个问题。
b. 可以 利用 padding = "SAME" 对输入尺寸有差异图像进行补齐，使得输入图像尺寸一致。
c. padding = "SAME" 可以使得卷积层的输入维度和输出维度一致。
⑤. 卷积核权重参数共享。
4. 反卷积
(1). 反卷积又称转置卷积 (Transposed Convolution)
可以看成是卷积层的前向传播过程就是反卷积的反向传播过程，卷积层的反向传播过程就是反卷积的前向传播过程。因为卷积层的前向、反向计算分别为 乘 
和 
(
)，而反卷积的前向、反向计算分别为 乘 和 ，所以它们的前向传播和反向传播刚好交换过来。
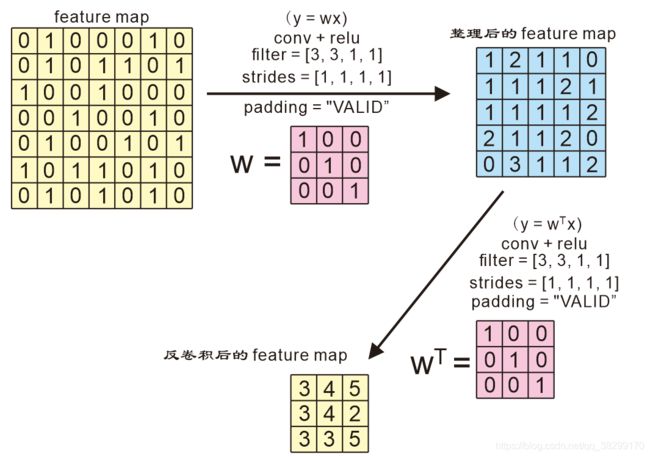
(2). 反卷积过程
①. 根据卷积核对 feature map 进行卷积，得到一个 new feature map。
②. 对 new feature map 进行非线性变化，得到所有整理后的 feature map。
③. 对整理后的 feature map 进行反卷积操作(如果卷积后有池化，就先反池化，再反卷积。池化和反池化，下一小节会说到)。
如果 padding = "SAME" 的话，反卷积后的 feature map 大小，和刚开始 的 feature map 是一样大小的。但是，值会变大，图像的轮廓会更清晰。
(3). 反卷积可视化各层得到的特征图作为输入，进行反卷积，得到反卷积结果，用以验证显示各层提取到的 feature map
5. CNN 卷积神经的优缺点
(1). 优点：
①. 共享卷积核，参数共享，使用稀疏连接。卷积神经网络通过这机制来减少参数，简化计算，节约内存资源，从而对高维数据处理无压力，即便使用更小的训练集来训练也能预防过拟合。
②. 无需手动选取特征，训练好权重，即得特征
③. 深层次的网络抽取图像信息丰富，表达效果好。
(2). 缺点：
①. 需要调参，需要大量样本集，训练最好使用 GPU
②. 物理含义不好理解，虽然我们了解一些核函数，比如说高斯核，图像经过高斯核处理后，就会得到高斯图像。但是，有很多卷积核 我们并不了解。所以，很多时候，我们并无法解释。
返回主目录
返回 CNN 卷积神经网络目录
下一章：深度篇—— CNN 卷积神经网络(二) 细说 池化 与 反池化