预测机械剩余使用寿命的深度可分离卷积神经网络

预测机械剩余使用寿命的深度可分离卷积神经网络

摘要

深度学习因其强大的表示学习能力在数据驱动的器械设备剩余使用寿命（RUL）预测中越来越受到重视。借助深度学习技术，可以更充分地了解机器退化情况，近年来的研究取得了卓有成效的机械设备剩余使用寿命的预测结果。然而，这些基于深度学习的预测方法有以下缺点：

1. 预测的准确度很大程度上取决于人工特征设计。
2. 在表示学习中，未明确考虑不同传感器之间数据的相关性。

为了克服上述缺点，本文提出了一种新的用于机械设备剩余使用寿命（RUL）预测的深度可分卷积网络（DSCN）。在所提出的DSCN中，不同传感器采集的监测数据直接作为网络的输入。然后，基于可分离卷积和压缩激励运算，构造了一个具有残差连接的可分离卷积构造块。通过叠加多个可分离的卷积构造块，从输入数据中自动学习高维表示。最后，通过将学习到的表示输入到完全连接的输出层来估计RUL。分别利用滚动轴承加速退化试验的振动数据和涡轮发动机的公共退化仿真数据对所提出的DSCN进行了验证。实验结果表明，所提出的DSCN能够基于原始的多传感器数据提供准确的RUL预测结果，并且优于现有的数据驱动的预测方法。

1.介绍

近年来，随着传感器技术、通信技术和计算机技术的发展，工业物联网技术被广泛应用于机器设备健康监测，在机器运行过程中，多个传感器采集了大量的检测数据。这种爆炸量的数据规模给机器的剩余使用寿命预测带来了新的机遇和巨大挑战。同时，由于现代机械系统的复杂性，很难建立基于第一原理或失效机理的精确的数学或物理预测模型[1,2]。因此，如何从海量的监测数据中充分挖掘出有价值的机器退化信息，并准确地建立相应的RUL预测模型，成为当前迫切需要研究的课题。由于数据驱动的RUL预测能够自动推断隐藏在数据中的因果关系，并能直接模拟复杂机械系统的退化特性，因此它可能是处理大量监测数据和提供准确RUL预测结果的有力解决方案[3,4]。

一般来说，数据驱动的RUL预测包括四个主要过程：数据获取、特征提取和选择、退化行为学习和RUL估计[1,5]。首先，安装在被监测机器上的各种传感器采集各种监测数据，如振动和声发射信号。然后，为了反映机器的健康状况，使用信号处理技术从采集的数据中提取代表性特征[6,7]。然而，其中一些人工特性可能对退化过程不敏感，甚至不能为RUL预测提供任何有用的信息。因此，特征选择是为了从所有人工特征中找到敏感的特征。之后，将所选特征输入到机器学习模型中，例如高斯过程回归（GPR）[8]、支持向量机（SVM）[9]和人工神经网络（ANNs）[10]，以学习机器的退化行为。最后，使用这些学习模型估计RUL。例如，Loutas等人[9]利用Spearman相关系数选取最单调的特征，并将这些特征输入$\epsilon$-SVM中，对滚动轴承的RUL进行预测。Javed等人[11]提出了一种基于单调性和趋势性的刀具和轴承故障预测方法，利用极值学习机进行RUL估计。Lim等人[12]提出了一种基于时间序列直方图的特征提取方法，从多传感器数据中提取出具有局部退化趋势的特征，并利用多层感知器对涡扇发动机的RUL进行估计。

近年来，深度学习在数据驱动的RUL预测中越来越受到重视。深度学习是机器学习的一个子集，它使用多层ANNs在各种分类或回归任务中提供最前沿的精确度。与传统的机器学习技术不同，深度学习技术，如深度信念网络（DBNs）[14]、卷积神经网络（CNNs）[15]和长期短期记忆（LSTM）网络[16]，能够从原始输入数据中自动学习多个层次的表示，而不需要引入手工编码规则或领域知识。由于这种强大的表征学习能力，深度学习在自动变速器[17]、语音识别[18]、自然语言理解[19]、药物探索[20]等领域[21,22]取得了巨大的成功。对于数据驱动的RUL预测，已经进行了一些基于深度学习的研究。Ren等人[23]采用自动编码器对36个时域特征进行融合，并将融合后的特征输入到深层神经网络中，对滚动轴承的RUL进行估计。Deutsch等人[24]从振动信号中提取了6个时频特征，并用DBN对弧齿锥齿轮的RUL进行了预测。Zhu等人[25]将小波变换与CNN相结合对方位RUL进行预测，首先利用小波变换提取时频特征，然后利用多尺度CNN对RUL进行估计。Zhao等人[26]利用CNN从采集的多传感器数据中提取局部稳健特征，利用双向LSTM预测刀具磨损深度。

虽然深度学习在机械的RUL预测方面取得了很好的结果，但现有的预测方法受到以下限制。

1. 它们的预测性能很大程度上取决于许多机器在RUL预测中的人工特征设计。相应地，为了获得敏感特征，需要在特征提取和选择上付出很大的努力。然而，这种程序需要明确的先验知识和大量的人力。特别是，用于预测的特征通常是逐个设计的，因此它们不能普遍应用于不同的工业案例。
2. 目前的深度预测模型没有明确考虑表征学习中不同传感器数据的相关性。不同传感器的数据包含不同程度的退化信息，反映了不同部件之间的故障交互作用。例如，由于频繁的连接，一个部件的故障可能会导致另一个部件的故障，而新的故障会使原来的故障更加严重。相应地，安装在组件上的传感器可以捕捉故障的传播和相互作用。因此，为了准确地预测RUL，重要的是捕捉不同传感器数据的相关性，并强调与机器健康状况最相关的信息。

针对上述局限性，本文提出了一种新的深度预测网络，即深度可分卷积网络（DSCN），用于机械设备的RUL预测。在所提出的DSCN中，不同传感器采集的监测数据直接作为预测网络的输入。然后，基于可分离卷积层和压缩激励(SE)单元，建立了可分离卷积构建块。通过叠加多个可分离的卷积构建块，可以从原始输入数据中自动学习高维表示。最后，通过将学习到的表示输入最后一个完全连接层来估计RUL。通过滚动轴承RUL预测和涡扇发动机RUL预测两个实例，验证了所提出的DSCN。实验结果表明，所提出的DSCN具有较高的RUL预测精度，优于传统的数据驱动方法和典型的深度学习模型。本文的主要贡献概括如下：

1. 将可分离卷积运算引入机械规则预测中。可分离卷积的引入不仅有效地模拟了不同传感器数据之间的相互关系，而且大大减小了预测网络的规模。
2. 构造SE单元，自适应地重新校准来自可分离卷积层的特征响应。动态特征响应重校准突出了信息特征映射，抑制了无用特征映射，提高了预测网络的信息鉴别能力。
3. 提出了一种新的深度预测网络DSCN，它是基于可分卷积和SE单元构造和叠加多个可分卷积构建块的方法。建议的DSCN能够基于原始的多传感器数据的机械提供准确的RUL估计，并优于现有的一些预测方法。

本文的其余部分安排如下。第2节简要介绍了标准卷积网络和残差连接。第3节详细介绍了用于机械规则预测的DSCN。在第4节中，利用滚动轴承加速退化试验的振动数据和公共商业模块化航空推进系统仿真（C-MAPSS）数据，分别验证了所提出的DSCN的有效性和优越性。最后，第5节得出结论。

2. 预备知识

在本节中，首先简要介绍了卷积神经网络的基本结构，然后复习了卷积网络的残差连接。

2.1 卷积神经网络

卷积神经网络，也称为CNNs或ConvNets，是一种特殊类型的深度前向网络，用于处理多个阵列数据，如时间序列信号、图像和音频频谱图。它们由几个不同类型的层构成，包括卷积层、池化层和完全连接层[15]。

1. 卷积层。卷积层是卷积网络的核心组成部分。卷积层由卷积操作和激活操作生成的不同特征映射组成。特征映射的每个神经元只通过一组称为核的权值连接输入量的一个局部区域。一个特征映射中的所有神经元共享同一个核，从而减少了模型的参数，使网络的实现更高效。从数学上讲，第$l$层卷积层的第$n$个特征图$x_n^l$可以通过$$x_n^l=\sigma (z_n^l)\text{\hspace{1em}(1)}$$$$z_n^l=k_n^l\ast x^{l-1}+b_n^l=\sum _{c=1}^C{k}_{n,c}^l\ast x_c^{l-1}+b_n^l\text{\hspace{1em}(2)}$$其中$z_n^l$是卷积运算的输出，$\sigma (\cdot )$是非线性激活函数，如sigmoid，tanh和整流线性单元（ReLU）[13]表示卷积算子，$k_n^l$是第n个卷积核，即第n个权重向量，$b_n^l$是偏差项，$x^{l-1}$是输入量，即前一层$l-1$层中的特征映射，C是输入通道的数目。

2. 池化层。池化层的目标是通过使用非线性下采样函数（如max pooling、average pooling和$L^2$-norm pooling）将语义相似的特征合并为一个特征。在每个输入特征映射上独立地执行池化操作，并输出先前特征映射的局部批处理的总结统计，从而减小表示的空间大小。在第$l$个池化层中，第$n$个特征图$x^{l-1}$可以通过下式获得$$x_n^l=pool(x_n^{l-1},p,s)\text{\hspace{1em}(3)}$$其中，$x_n^{l-1}$是第$l$个池化层的第$n$个输入特征图，即前一层第$l-1$层的第$n$个特征图，$pool(\cdot )$是降采样函数，$p$是池化尺寸，$s$是条带大小。

3. 全连接层。全连接层原则上与传统的多层感知器相同，每个神经元都与前一层的所有神经元完全连接。一般来说，全连接层被用作卷积网络的输出层来执行高级推理。对于第$l$个完全连接层，其输出$x^l$可以下式通过计算$$x^l=\sigma (w^l{x}^{l-1}+b^l)\text{\hspace{1em}(4)}$$其中$x^{l-1}$是第$l$个全连接层的输入，即前一层第$l-1$层的输出，$w^l$是权重矩阵，$b^l$是偏移向量。

2.2. 卷积网络的残差连接

残差连接首先由He等人提出。在[27]中，旨在减少卷积网络的训练复杂度并能使网络大大加深。网络的深度，即层数对提高卷积网络的表示能力起着至关重要的作用。但随着网络深度的增加，训练难度增大，训练精度趋于饱和甚至急剧下降。为了解决这个问题，在文献[27]中，对卷积网络引入了残差连接。在卷积构建块中，通过在输入和输出之间添加一个特征捷径来建立残差连接。相应地，具有残差连接的构建块不是学习无关映射，而是学习相对于输入的剩余映射，这比原始映射更容易优化。同时，残差连接既不增加额外的参数，也不增加计算复杂度。更重要的是，使用残差连接的卷积网络能够通过增加网络深度轻松实现性能改进。形式上，让$\mathcal{H}(x^{l-1},W^l)$表示具有残差连接的构建块的所需底层映射，然后该构建块中的堆叠权重层将适合$\mathcal{F}(x^{l-1},W^l):=\mathcal{H}(x^{l-1},W^l)-x^{l-1}$的剩余映射。相应地，构建块的输出可以表示为： $$x^l=x^{l-1}+\mathcal{F}(x^{l-1},W^l)\text{\hspace{1em}(5)}$$其中，$x^{l-1}$和$x^l$分别是构建块的输入和输出，$\mathcal{F}(\cdot )$是残差函数，例如，两个卷积层的堆栈，$W^l=(W_1^l,W_2^l,\dots ,W_L^l)$是可学习层参数，即权重和偏差，$L$是构建块中的堆栈层数。

3 机械设备RUL预测的DSCN方法

本节详细介绍了用于机械RUL预测的DSCN。提出的DSCN直接利用来自不同传感器的监测数据作为输入。然后，为了有效地建模不同传感器数据之间的相互关系，引入可分离卷积来代替标准卷积。同时，为了提高DSCN对信息特征映射的敏感度，在可分离卷积层的后面构造了一个新的结构单元SE单元来进行自适应的特征响应重新校准。然后，利用可分离卷积和SE单元构造DSCN的核心构造块可分离卷积构造块。通过叠加多个可分离的卷积构建块，从输入数据中学习高维表示，最后通过将学习到的表示输入到一个全连接层中来估计RUL。

3.1 可分离卷积

为了集成来自不同传感器的退化信息，多通道时间序列数据通常被用作深度预测模型的输入，其中每个通道代表一个传感器序列。对于这些多传感器时间序列输入数据，每个通道中的数据都具有时间相关性，因为它们是由同一个传感器采集的，反映了一个被监测部件在运行时间内的故障进展。同时，由于故障在不同元件间的传播和相互作用，不同通道中的数据也具有跨通道相关性。然而，现有的深度预测模型同步映射时间相关性和交叉信道相关性来模拟机械的退化过程[26,28-30]，因此不能有效地捕获和建模不同传感器数据的依赖关系，这限制了预测模型的预测精度及其推广。因此，本文将可分离卷积运算[31]引入机械RUL预测中，代替了公式(2)中描述的标准卷积运算，目的是通过分离时间相关性和交叉通道相关性，有效地建模不同传感器数据之间的相互关系。

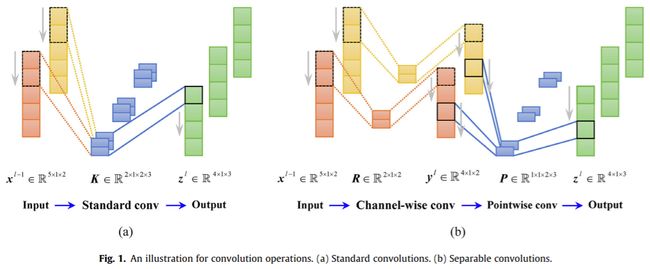
可分离卷积通过分解标准卷积来分解时间关联和跨通道关联。如Fig.1所示，标准卷积被分解为两部分：通道卷积和点卷积。首先，通道卷积将单个卷积核应用于每个输入信道，以分别映射每个传感器序列的时间相关性。然后，逐点卷积执行$1\times 1$卷积以创建逐通道卷积的输出的线性组合，即映射不同传感器的跨通道相关性。通过上述两个独立的步骤，时间相关性和跨信道相关性可以充分地解耦。具体来说，可分离卷积使用特定的卷积核，即逐点卷积核来映射跨通道相关性，从而有效地捕获不同传感器数据的相关性。

设$x^{l-1}\in {\mathbb{R}}^{H\times W\times C}$表示输入量，其中$H$和$W$分别是输入量的高度和宽度，$C$是输入通道数。特别是对于多传感器输入数据，例如来自不同加速器的振动信号，$H$是每个传感器序列的长度，$W$等于1，$C$是传感器的数目。相应地，标准卷积层中的卷积核表示为$K\in {\mathbb{R}}^{M\times 1\times C\times N}$，其中$M\times 1$是卷积核的大小，$N$是核的数目，即输出信道的数目。在可分卷积中，$K$被分解为信道卷积核$R\in {\mathbb{R}}^{M\times 1\times C}$和点卷积核$P\in {\mathbb{R}}^{C\times N}$。因此，可分卷积的第n个输出$z_n^l$可以由 $$y_c^l=R_c\ast x_c^{l-1}+b_c^l\text{\hspace{1em}(6)}$$ $$z_n^l=\sum _{c=1}^C{P}_n\ast y_c^l+b_n^l\text{\hspace{1em}(7)}$$

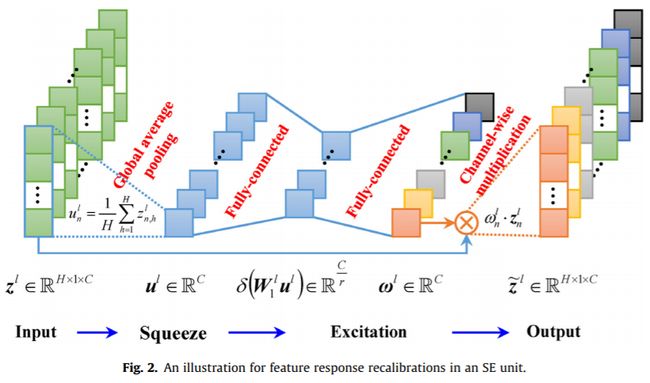
3.2 特征响应重新校准

可分离卷积层中的特征映射包含不同程度的代表性信息。因此，这些特征图中的一些可能是信息性的，但其他的可能不是。为了突出信息特征映射，抑制无用特征映射，在可分离卷积层后面构造了一个SE单元。如Fig.2所示，SE单元能够通过评估每个特征映射的信息性来自适应地重新校准其响应。具体来说，特征响应再校准过程包括挤压和激励两个步骤。首先，挤压操作将可分离卷积层的所有输出信道的全局信息嵌入到信道描述符$u^l\in {\mathbb{R}}^C$中。这一步是通过使用全局平均池化来缩小卷积输出$z^l$来实现的，其中$u^l$由$N$个信道统计组成，$u^l$的第N个元素可以通过下式计算 $$u_n^l=\frac{1}{H}\sum _{h=1}^H{z}_{n,h}^l\text{\hspace{1em}(8)}$$
然后，激励操作利用自动门机制[32]基于信道描述符$u^l$估计每个信道的信息性，生成相应的信道权重$w^l$，即$$w^l=\sigma (W_2^l\delta (W_1^l{u}^l))\text{\hspace{1em}(9)}$$ 其中$\sigma (\cdot )$和$\delta (\cdot )$分别为sigmoid函数和ReLU激活函数，$W_1^l\in {\mathbb{R}}^{\frac{C}{r}\times C}$和$W_2^l\in {\mathbb{R}}^{C\times \frac{C}{r}}$为权重，$r$为降维比。为了限制计算复杂度，通过两个完全连接的层，包括具有$\frac{C}{r}$个神经元的维度缩减层和具有$C$个神经元的维度增加层来对自动门(self-gating)机制进行参数化。最后，通过将可分离卷积的特征映射$z_n^l$与相应的信道权值$w_n^l$进行信道相乘，得到重新校准的特征映射。

3.3 可分卷积构建块

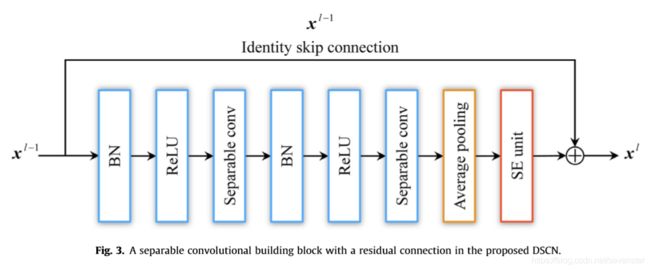
如第2.2节所述，通过叠加更多的权重层可以增强卷积网络的表示能力。然而，网络深度的增加使得训练更加困难，导致精度饱和甚至降低[27]。因此，本文采用残差连接来简化DSCN的训练。同时，文[33]中的预激活策略也被用来改善DSCN的正则化，从而缓解过拟合问题。Fig.3示出了在所提议的DSCN中具有残差连接的可分离卷积构建块，其中在输入$x^{l-1}$和输出$x^l$之间添加了标识跳过连接。可分离卷积构造块由两个可分离卷积层、一个平均池化层和一个SE单元组成。特别地，批处理规范化（BN）[34]和ReLU[35]都用作预激活，并在每个可分离卷积之前添加。

在可分离卷积构建块中，BN的使用是为了使每个可分离卷积的输入分布更加稳定，并减少过度拟合[34]。此外，BN允许DSCN使用更高的学习率，并对参数初始化不敏感。对于输入$x^{l-1}=(x_1^{l-1},x_2^{l-1},\dots ,x_C^{l-1})$，BN对每个输入信道$x_C^{l-1}$执行规范化，BN的转换可以写成$${\hat{x}}_c^{l-1}=\frac{x_c^{l-1}-{\mu }_B}{\sqrt{{\sigma }_B^2+\epsilon }}\text{\hspace{1em}(10)}$$$$y_c^{l-1}={\gamma }_c{\hat{x}}_c^{l-1}+{\beta }_c\text{\hspace{1em}(11)}$$式中，$y_c^{l-1}$为$x_c^{l-1}$对应的变换输出，${\mu }_B$和${\sigma }_B^2$分别为第$c$个输入通道中的小批量$B$的期望值和方差，$\epsilon$是一个为了数值稳定性而加到${\sigma }_B^2$上的常数，${\gamma }_c$为BN变换中的第$c$个可学习尺度参数，${\beta }_c$为第$c$个可学习移位参数。

一般来说，在标准卷积网络中，BN和ReLU是在卷积操作之后添加的，但是这种后激活策略可能无法充分利用BN在具有剩余连接的卷积网络中的好处[33]。因此，本文采用完全预激活策略l，即在每次可分离卷积之前进行BN和ReLU。此外，为了减小表示的维数，在SE单元之前插入一个平均池化层来执行降采样。随后，由SE单元重新校准的特征映射被添加到标识映射$x^{l-1}$以生成可分离卷积构建块$x^l$的输出，然后将其反馈到下一可分离卷积构建块或后续处理层。

3.4 建议的DSCN的体系结构

Fig.4展示了所提出的DSCN的架构，其中输入是由不同传感器获取的监视数据，输出是相应的RUL值。DSCN由两个子网组成，即表示学习子网和RUL估计子网。表示学习子网能够通过叠加多个可分离的卷积构建块，自动发现判别信息，从输入数据中学习多个层次的表示，将学习到的高维表示输入RUL估计子网，通过全连接层进行RUL预测。DSCN的更多细节如下。

1. 表示学习子网络首先使用可分离卷积层卷积尺寸为$H\times 1\times C$的输入传感器数据，其中信道卷积核的大小被设置为$M\times 1$，点卷积核的数量即输出信道的数量被设置为$N$，而BN和ReLU都是在可分离卷积之后采用的。在可分离卷积层之后，使用平均池化层进行降采样，其中池大小$p$等于步长$s$。然后，将学习到的低层表示转发到后续可分离卷积构建块以获得更高层表示。对于第$d$个可分离卷积构建块，其中$d=1,2,\dots ,D$，两个可分离卷积层的配置是相同的，即每个信道级卷积核具有$M\times 1$大小，并且每个可分离卷积层中包含总共$2^{d}N$个点卷积核。此外，平均池化是使用非重叠窗口，即$p=s$来执行的，并且通过考虑预测精度和计算复杂度之间的折衷，SE单元中的维数减少率$R$设置为16，这将在4.1.5节中讨论。

2. RUL估计子网利用全局平均池化层从表示学习子网接收高维表示，即第D个可分离卷积构建块的输出。相应地，将来自第D个可分离卷积构建块的$2^{D}N$输入特征映射转换为$2^{D}N$大小的向量。需要注意的是，使用全局平均池是为了减少参数总数。在此基础上，采用全连接层作为DSCN的输出层来估计RUL，其中在网络的末端只连接一个神经元，并采用ReLU实现非线性激活。

4. 实验验证

为了验证所提出的DSCN在处理机械部件或系统退化问题方面的有效性和优越性，本节进行了两个实例研究，包括：

1. 滚动轴承的RUL预测；
2. 涡扇发动机的RUL预测。

在第一个案例研究中，使用从轴承加速退化试验中收集的振动信号来评估DSCN的预测性能，并使用四种最新的预测方法进行比较。在第二个案例研究中，使用预测基准数据集（即公共C-MAPSS数据集）进一步验证了所提出的DSCN，并与使用相同验证数据集的6个已发表研究进行了比较。

4.1 案例研究1：滚动轴承加速退化试验

4.1.1 数据描述

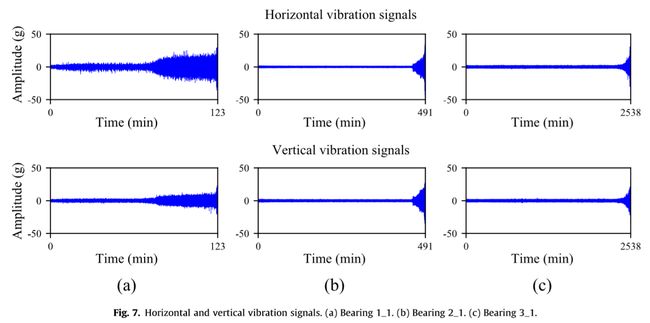
Fig.5显示了由交流（AC）电机、电机速度控制器、支撑轴、两个支撑轴承（重型滚柱轴承）、液压加载系统等组成的滚动轴承试验台[36]。该试验平台能够对不同工作条件下的轴承进行加速退化试验，获得完整的运行失败数据。如Table 1所示，本文共对15个LDK-UER204滚珠轴承在三种不同的工作条件下进行了试验。径向力由液压加载系统产生，施加在被测轴承的外壳上，转速由交流感应电动机的速度控制器设定和保持。Fig.6显示了正常和降级轴承的照片。可以观察到，被测轴承的故障是由不同类型的故障引起的，包括内圈磨损、保持架断裂、外圈磨损、外圈断裂等，采集被测轴承的振动信号，如Fig.5所示，PCB-352C33型两个加速度计位于测试轴承的壳体的90°处，即一个置于水平轴上，另一个位于垂直轴上。采样频率设置为25.6kHz，每1分钟记录32,768个数据点（即1.28s）。Fig.7描绘了三种不同操作条件下的水平和垂直振动信号。本文选取各工作情况的前4个轴承数据集作为训练数据集，其余为测试数据集。特别地，水平和垂直振动信号都被用作DSCN的输入。

4.1.2 评价指标

本文利用评分函数和均方根误差（RMSE）对DSCN的预测性能进行了定量评价。

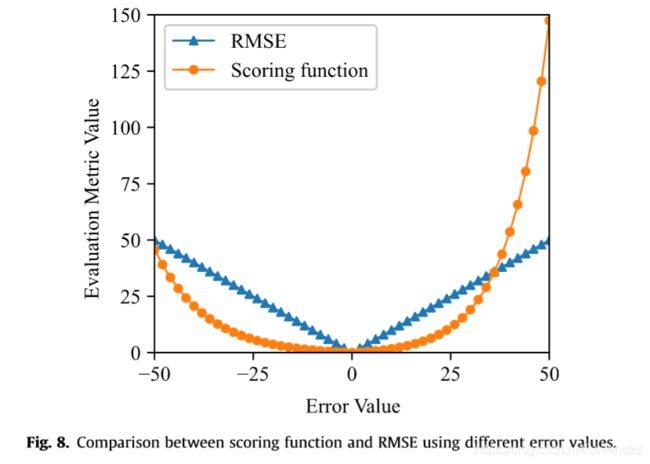
1. 评分函数：本文使用的评分函数来自《2008年预测与健康管理数据挑战》[37]，定义为$$score=\{\begin{array}{ll}{\sum }_{i=1}^Q(e^{-\frac{d_i}{13}}-1)& \text{for }{d}_i<0\\ {\sum }_{i=1}^Q(e^{\frac{d_i}{10}}-1)& \text{for }{d}_i\ge 0\end{array}\text{\hspace{1em}(12)}$$其中，$score$是RUL预测结果的得分值，$Q$是测试样本的数量，$d_i=PreRU{L}_i-ActRU{L}_i$是相对于第i个测试样本的估计RUL和实际RUL之间的误差。Fig.8示出了评分函数，其中误差值范围从-50到50，间隔为2。从Fig.8可以看出，绝对误差值越小，得分越低。此外，评分函数是不对称的，因此迟预测（即$d_i\ge 0$）比早预测（即$d_i<0$）受到更严重的惩罚。但是，应该注意的是，由于惩罚随着误差的增加呈指数增长，分数可能完全由一个具有非常大预测误差的孤立点支配。为了解决这个问题，本文引入RMSE作为第二个性能评价指标。
   
   
   
   

2. RMSE：RMSE是预测和健康管理领域常用的评价指标。给定RUL预测结果，RMSE值由$$RMSE=\sqrt{\frac{1}{Q}\sum _{i=1}^Q{d}_i^2}\text{\hspace{1em}(13)}$$ Fig.8还示出RMSE作为误差的函数。可以看出，与评分函数不同的是，RMSE给每个预测分配了相等的权重，从而避免了异常值的干扰。
   

4.1.3 数据预处理

1. 标准化：对于水平和垂直振动信号，在每个采样时间点采集的数据使用z-score标准化，即$$x_{norm}^t=\frac{x^t-{\mu }^t}{{\sigma }^t}\text{\hspace{1em}(14)}$$ 式中，$x^t$表示在第t个采样时间步骤采集的原始振动信号，$x_{norm}^t$表示与$x^t$对应的归一化振动信号，${\mu }^t$和${\sigma }^t$分别表示$x^t$的平均值和标准偏差。此外，需要注意的是，被测轴承的使用寿命范围非常广（从33分钟到2538分钟）。如果在训练期间使用每个采样时间步的实际RUL值作为DSCN的期望输出，则寿命的显著差异将导致欠拟合的问题[38]。因此，在数据预处理过程中，将训练数据集中的每个轴承的实际RUL值除以其各自的轴承寿命，使其在[0,1]的范围内规范化也是一个重要步骤。然后，使用这些标准化的RUL值作为DSCN的目标输出。相应地，根据RUL[39]的定义，测试数据集中每个轴承的估计RUL值可以通过$$PreRU{L}_t=\frac{NormRU{L}_t}{1-NormRU{L}_t}\times P_t\text{\hspace{1em}(15)}$$其中，$P_t$是与第$t$个采样时间步骤相对应的检查时间，$NormRU{L}_t$是在$P_t$处训练的DSCN的预测值，$PreRU{L}_t$是在$P_t$处估计的RUL。
2. 时间窗嵌入：对于数据驱动的预测问题，如何将有用的时间信息嵌入到预测模型的输入中是一个重要的考虑因素。如果预测模型仅使用在单个采样时间步获得的数据作为输入，则会忽略与当前退化状态相关的先前时间信息，从而限制模型的预测性能。针对这一问题，本文采用时间窗嵌入策略[40]对归一化后的被测轴承振动信号进行处理，其中，利用固定大小的时间窗将在连续采样时间步处获得的振动信号串接成高维向量，然后将该向量作为输入馈入DSCN。因此，在每个采样时间步，通过时间窗嵌入获得的输入向量由在当前时间步采样的振动信号及其之前的$S-1$个时间步组成，可以表示为$$x_{input}^t=(x_{norm}^{t-S+1},\dots ,x_{norm}^{t-1},x_{norm}^t)\text{\hspace{1em}(16)}$$其中$S$是时间窗口的大小。Fig.9显示时间窗嵌入的示例，其中，在每个时间步，使用大小为3的时间窗将振动信号封装到输入向量中。

4.1.4 DSCN的配置

在所提出的DSCN中，需要预先定义的超参数包括信道卷积核大小$M\times 1$、点卷积核数目$N$、池化大小$p$、SE单元的降维比例$r$和可分离卷积构建块数目$D$，这些超参数是通过对训练数据集进行4折交叉验证来确定的，Table 2列出了最终的超参数选择结果，这是通过考虑权衡预测精度和计算成本来确定的。特别是下面4.1.5节将详细讨论压缩比$r$和块数$D$对DSCN预测性能的影响。此外，还利用一个大小为5的时间窗来处理归一化振动信号。这里，每个归一化信号序列$x_{norm}^t$包含2560个数据点，相应地，输入量的大小为$12800\times 1\times 2$。在训练过程中，采用均方误差（MSE）作为DSCN的损失函数，采用最小批量为128的Adam优化器[41]迭代更新网络权值和偏差，使MSE损失函数最小化。该模型从头开始训练100个阶段，并使用[27]中描述的策略初始化权重和偏差。

4.1.5 实验结果

在本研究中，首先详细探讨了影响DSCN预测性能的一些因素，包括时间窗大小、降维率和网络深度。然后，分析和讨论了可分离卷积和特征响应重新校准的优点。最后，将所提出的DSCN与四种最新的预测方法进行了比较，以证明其优越性。以下研究中的每个实验重复20次，以减少随机性的影响。特别是，对于测试数据集中的每个轴承，得分和RMSE是从使用寿命的一半到结束计算的，因为在这些检查时间实例中的预测比早期阶段更可靠和更有意义[42]。

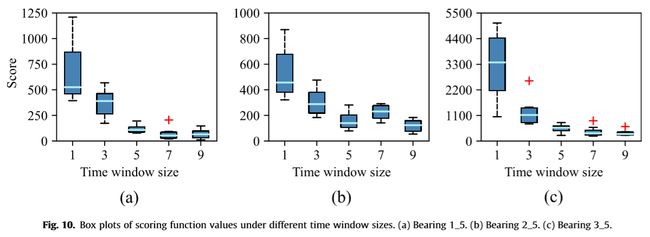
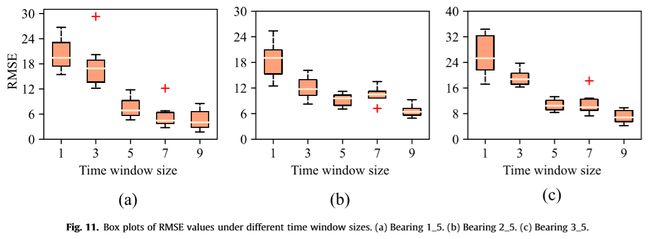
1. 时间窗嵌入分析：如前所述，时间窗嵌入能够将更多有用的退化信息收集到DSCN的输入中，从而提高其预测性能。特别是，这种性能改进与时间窗口大小有关。因此，本章首先分析了不同时间窗大小对DSCN预测性能的影响。对于方位的RUL预测，时间窗大小S分别设置为1、3、5、7和9。相应地，Fig.10和11中分别示出了三个被测轴承的评分函数值和RMSE值的方框图。从这些方框图中可以看出，时间窗越大，得分和RMSE值越低，这意味着增加时间窗的大小可以有效地提高DSCN的预测性能，从而聚集更多关于轴承退化的时间序列信息。此外，Fig.12展示了6种不同时间窗大小下的轴承3_5的RUL预测结果。可以清楚地看到，时间窗口大小的增加使得RUL预测更加准确，同时减少了RUL估计值的波动。但是，应该注意的是，随着时间窗口大小的增加，不仅性能改进的空间逐渐减小，并需要更多的内存存储和计算时间，因为大的时间窗口大小将生成高维的输入向量。在上述分析的基础上，将时间窗的大小$S$设定为5。

2. 降维率和网络深度的影响：降维率$r$是SE单元中的一个重要超参数，其大小可能影响SE单元的容量和计算成本。为了研究这种影响，采用不同降维比的DSCN对轴承进行RUL估计，最终估计结果见Table 3。可以看出，虽然维数降低率的增加减少了模型的总参数和训练时间，但DSCN的性能并不能单调地得到改善。特别是当降维率为16时，预测模型在精度和计算成本之间取得了很好的折衷。因此，本文将降维率$r$设为16。此外，本节还研究了网络深度对DSCN预测性能的影响。对于所提出的DSCN，可以通过堆叠更多可分离的卷积构建块来增加网络深度。这里，总共研究了五种不同的网络深度，相应的性能估计结果总结在Table 4中。从这个表可以看出，深度预测网络在轴承的RUL预测中得分较低，RMSE值较小。这意味着网络深度的增加提高了DSCN的表示学习能力。然而，更深的体系结构将导致更重的计算负担。同时，随着预测网络的加深，有限的训练样本可能导致过拟合[28]。因此，本文将可分离卷积构造块个数$D$设为3。

3. 可分离卷积和特征响应重校准的优点：为了说明第3节中描述的可分离卷积和特征响应重新校准的优点，在本节中还使用其他两个预测网络来展示RUL预测的影响，包括标准卷积网络（表示为标准ConvNet）和可分离卷积网络（表示为可分离ConvNet）。除了不包含SE单元外，这两个预测网络具有与所提出的DSCN相同的架构和超参数设置。Table 5报告了这三种不同预测网络的总模型参数和训练时间。可以看出，与标准卷积相比，可分离卷积大大减小了模型的尺寸（减少了82.07%），从而降低了计算成本。而对于所提出的DSCN，与可分离ConvNet相比，SE单元的引入只增加了5.50%的参数。Fig.13示出了这三种不同的预测网络的性能估计结果。可见，可分离ConvNet对每个方位的得分都低于标准ConvNet，RMSE值也小于标准ConvNet，这意味着通过充分分离时间相关性和跨通道相关性，可分离卷积有效地提高了预测网络的性能。此外，通过使用SE单元自适应地重新校准来自可分离卷积层的特征响应，所提出的DSCN比其他两个预测网络获得更好的预测性能。因此，得益于可分离卷积和SE单元，与标准卷积网络相比，所提出的DSCN在精度和计算复杂度方面具有明显优势。接下来，通过与四种最新的预测方法的比较，进一步证明所提出的DSCN的优越性。
   

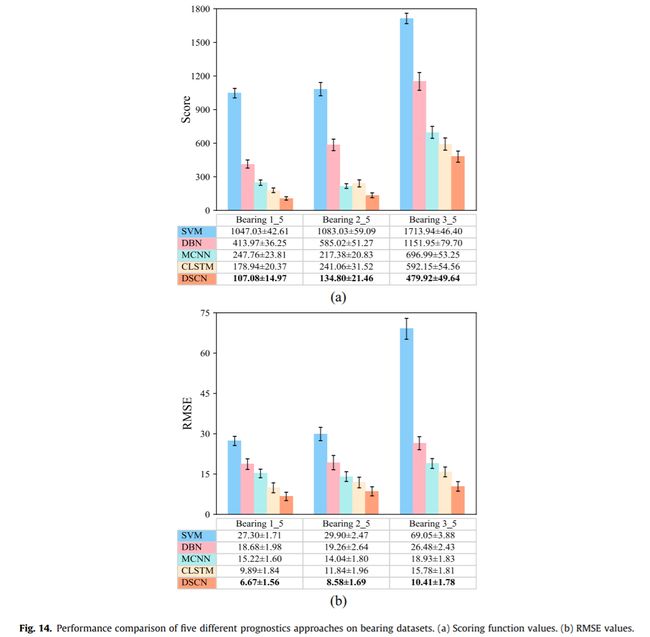
4. 与最先进的预测方法的比较：在本节中，四种现有的预测方法实现用来预测所测试的轴承的剩余使用寿命RUL从而进行比较，包括SVM[9]、DNB[24]、多尺度CNN（MCNN）[25]和卷积LSTM（CLSTM）[26]。对于前三种预测方法，即SVM、DBN和MCNN，特征提取和选择首先按照[9、24、25]进行。然后，将选定的特征输入到相应的模型中进行训练和测试。而对于CLSTM，首先利用单层CNN从轴承振动信号中提取局部鲁棒特征，然后将这些特征输入到双向LSTM中进行RUL估计。特别是，为了获得更准确的RUL预测结果，还对每个预测模型进行了4折交叉验证，实现了超参数调整。
   
   
   
   
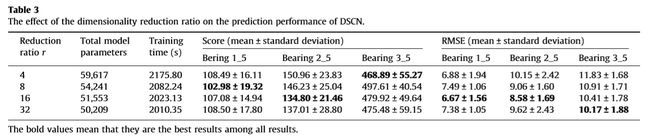
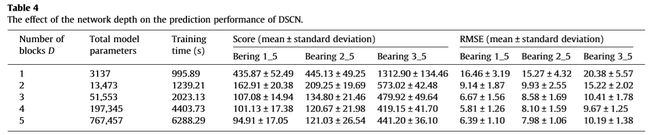
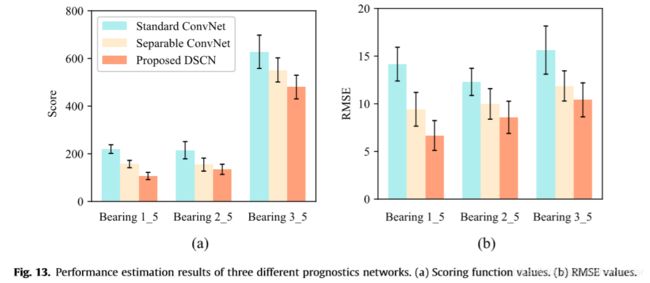
   Fig.14总结了这五种不同预测方法的性能估计结果。第一个观察是，对于三个被测轴承中的每一个，深度学习模型（即DBN、MCNN、CLSTM和DSCN）在得分和RMSE方面都始终优于传统的机器模型（即支持向量机）。这是因为传统的机器学习模型是建立在浅层学习结构上的，因此它们学习轴承退化行为的能力有限。相反，深度学习模型由于其突出的表示学习能力，能够更好地挖掘有价值的轴承退化信息，建立更准确的RUL预测模型。此外，从Fig.14可以观察到，所提出的DSCN在所有深度预测模型中获得最低得分值和最小RMSE值，这表明DSCN为每个轴承提供最准确的RUL估计结果。因此，本文提出的DSCN方法在轴承规则预测方面优于其他四种预测方法。这种性能改进再次验证了可分离卷积和特征响应重新校准的好处。
   

4.2. 案例研究2：公共C-MAPSS数据集

4.2.1 C-MAPSS数据集

为了进一步验证所提出的DSCN的有效性和优越性，在本案例研究中使用了预测基准数据集，即C-MAPSS数据集。C-MAPSS数据集由美国宇航局Ames研究中心的卓越预测中心（PCoE）提供，可在PCoE的预测数据存储库网站上查阅[43]。如Table 6所示，C-MAPSS数据集由四个子数据集组成，在不同的工作条件和故障模式组合下进行模拟。利用C-MAPSS软件对涡扇发动机进行了运行失效模拟，采集了21个传感器的监测数据，反映了涡扇发动机的失效过程。特别地，每个子数据集被分为一个训练数据集和一个测试数据集。对于训练数据集，提供完整的运行到故障数据，包括多传感器测量和相应基本事实的RUL值。而对于测试数据集，则对每台涡扇发动机的监测数据进行截断，以预测RUL。

4.2.2 预测结果、比较与讨论

在退化模拟过程中，共有21个变量从C-MAPSS模型输出。这些变量代表涡扇发动机系统各部件的传感器响应。然而，其中一些设备整个工作期间的寿命具有恒定值，因此不能为RUL预测提供任何有用的退化信息。因此，首先在[44]之后进行传感器选择，其中选择14个传感器作为预测模型的输入。然后，使用最小-最大度量[28]对所有传感器数据进行标准化。此外，在数据预处理中还采用了大小为30[28]的时间窗口和分段线性退化假设[45]。相应地，DSCN的输入量大小为$30\times 1\times 4$。

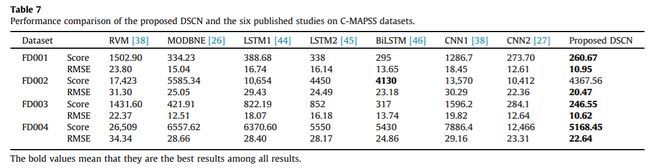
在涡扇发动机的RUL预测中，除了时间窗大小外，所提出的DSCN使用Table 2中列出的相同配置。同时，将得分函数和RMSE作为绩效评价指标。此外，为了说明所提出方法的优越性，本文还将DSCN的预测结果与文献[40]中的相关向量机（RVM）和经典CNN（CNN1）的预测结果、文献[28]中的多目标深度信念网络集成（MODBNE）的预测结果进行了比较，[46]中的LSTM结果（表示为LSTM1）和[47]中的LSTM结果（表示为LSTM2）、[48]中的双向LSTM结果（表示为BiLSTM）和[29]中的无池化层CNN的结果（表示为CNN2）。Table 7显示了在C-MAPSS数据集上，文中所提出的DSCN与6个已公布的研究方法的性能比较结果。可以清楚地看到，与其他预测方法相比，对于每个子数据集，DSCN的得分值更低，RMSE值更小，这意味着DSCN在涡扇发动机RUL预测中表现得更好。此外，值得注意的是，与FD001和FD003相比，其余两个子数据集具有更高的得分值和更大的RMSE值。这是因为FD002和FD004的子数据集是在六种不同的操作条件下模拟的，这增加了预测问题的复杂性。特别是，对于[40]和[29]中的两个典型卷积网络，增加的复杂度使得表示学习更加困难，导致比其他常用的深度学习模型（即MODBNE、LSTM和BLSTM）更高的预测得分值。而对于卷积网络，由于可分离卷积的使用和SE单元的建立，即使预测问题的复杂性增加，仍能获得相对好的精确度。基于上述两个案例研究，得出的结论是，所提出的DSCN能够精确地基于原始多传感器数据对机器的退化过程建模，并与现有的预测方法相比，具有更好的预测性能。

5. 结论

本文提出了一种新的深度预测网络DSCN，用于机械设备的RUL预测。提出的DSCN直接利用原始的多传感器数据作为预测网络的输入。然后，引入可分离卷积运算代替标准卷积运算，有效地模拟了不同传感器数据之间的相互关系。同时，为了提高预测网络对信息特征映射的敏感性，在可分离卷积层后面构造一个SE单元进行自适应特征响应重新校准。然后，基于可分离卷积和SE单元构造可分离卷积构建块。特别地，在可分离卷积构建块中还采用了剩余连接和预激活，以简化网络的训练和缓解过拟合问题。通过叠加多个可分离的卷积构建块，从输入数据中学习高层表示，最后通过将学习到的表示反馈到最后一个完全连接层来估计RUL。利用滚动轴承加速退化试验的振动数据和公开的C-MAPSS数据集对所提出的DSCN进行了实验验证，并与目前的一些预测方法进行了比较。实验结果表明，所提出的DSCN具有较高的RUL预测精度，优于传统的数据驱动方法和典型的深度学习模型。

文中总结了DSCN在实际应用中的优点。

1. 提出的DSCN直接利用原始多传感器数据作为输入，摆脱了人工特征提取和选择的复杂过程。事实上，许多现有的深度预测网络仍然需要从原始传感器数据中手动提取和选择一些带偏见的特征。然而，这种程序既费时又费力，同时需要明确的先验知识和专业知识。此外，用于预测的特征通常是逐个案例设计的，它们的泛化能力可能很弱。因此，在实际应用中，直接利用原始传感器数据作为深度预测网络的输入是非常重要和有意义的。
2. 在工业应用中，一台机器通常由多个传感器进行监控。因此，获得的多传感器数据具有两个不同的特征。一种是不同的传感器数据包含不同程度的退化信息，其中一些传感器数据可能对机器退化敏感，但另一些可能不敏感。另一方面，这些传感器数据能够捕捉故障在不同部件之间的传播和相互作用。

在提出的DSCN中，这些修正在网络建设过程中得到了充分的考虑。首先引入可分离卷积来建模不同传感器数据之间的相互关系，然后构造SE单元来强调重要的退化信息。因此，在实际应用中，所提出的DSCN能够有效地提高预测精度。