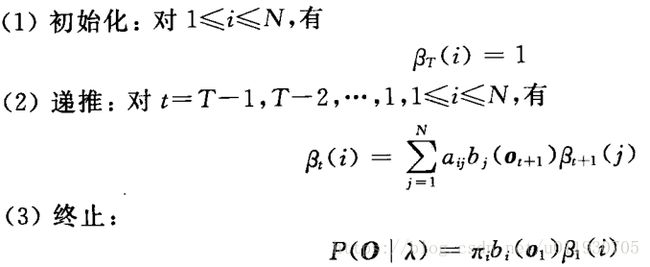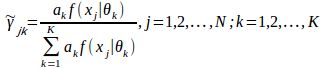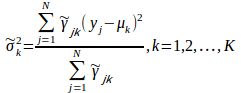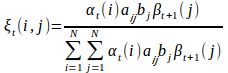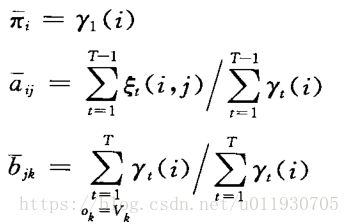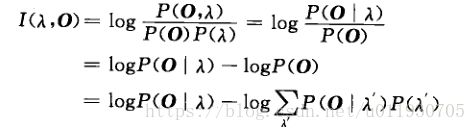HMM隐马尔可夫模型学习总结

1. 介绍

1. HMM在实际应用中主要用来解决3类问题。

1.评估问题(概率计算问题)

即给定观测序列 O=O1O2…Ot和模型参数λ=(A,B,π)，怎样有效计算这一观测序列出现的概率P(O|λ)

2.预测问题 (也称解码问题)

即给定观测序列 O=O1O2…Ot和模型参数λ=(A,B,π)，怎样寻找满足这种观察序列意义上最优的隐含状态序列S。

3.学习问题。

即HMM的模型参数λ=(A,B,π)未知，如何求出这3个参数以使观测序列O=O1O2…Ot的概率尽可能的大,可以使用极大似然估计参数(EM算法)。

4.个人理解

通过Baum-Welch训练HMM模型，然后输入需要判断的数据通过前向后向算法计算确定属于哪个模型，最后通过viterbi解码隐含状态序列 

1. 前向算法

• 问题：给定观察值序列O=o1,…,oT以及一个模型λ=(π,A,B ) 时产生出O的概率P(O|λ)？

• 前向向量定义：at(i) = P(o1 o2 …ot,qt=i|λ)

• 前向算法过程如下：

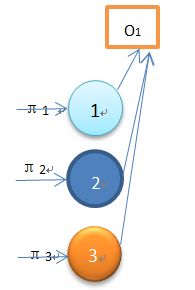
（1）初始化：a1(i) = πibi(O1), 1≤i≤N

（2）递推:

,1≤j≤N,1≤t≤T-1

t+1时刻状态j的概率值为t时刻每一个状态的概率值与其对应转移函数相乘的累积和再与观察值概率相乘

（3）终止:

其中：

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

• 下面解释这个算法：

该图为初始状态，输出观察值为O1 ，图中显示3个状态对应算法初始化公式，而该序列观察值所得概率为：

     P(O1| ）= π1b1(O1)+π2b2(O1)+π3b3(O1)=α1(1)+α1(2)+α1(3)

该图为一次递推过程，输出观察值为O1 O2，图中O2对应的状态1的概率是通过O1对应的3个状态通过递推公式求得，该结果为：

P(O1 O2,q2=θ1| ）= α1(1)a11b1(O2)+ α1(2)a21b1(O2)+ α1(3)a31b1(O3)

以此类推可以得到P(o1 o2 …ot|λ)

• 前向算法计算P(O|M)过程：

step1： α1(1) =π1b1(red)=0.2*0.5=0.1

α1(2)=π2b2(red)==0.4*0.4=0.16

α1(3)=π3b3(red)==0.4*0.7=0.21

step2：α2(1)=α1(1)a11b1(white)+α1(2)a21b1(white)+α1(3)a31b1(white)

...

step3:P(O|M) = α4(1)+α4(2)+α4(3)

前向算法实现代码参考此链接：

http://blog.csdn.net/u011930705/article/details/77372820 

1. 后向算法

• 后向向量定义：βt(i) = P(ot+1 ot+2 …ot+T |qt=i,λ)

βt(i)：t时刻状态i的概率值为t+1时刻的每个状态与其对应的转移函数和对应的观察值概率相乘的累加和的值。

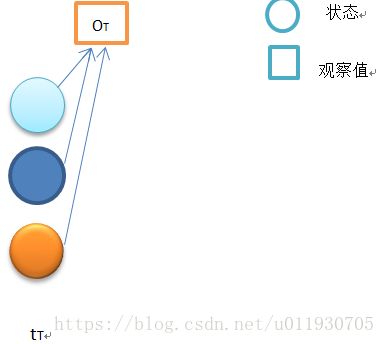
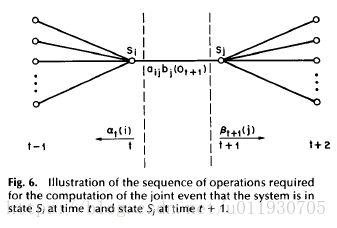
• 下面解释这个算法：

初始状态如上图，当t=T时，按照定义：时间t 状态qT 输出为OT+1......的概率，由于从T+1开始的输出是不存在的（T时刻是终止终止状态），即T之后是空，是个必然事件，因此βt(i)=1,1≤t≤N

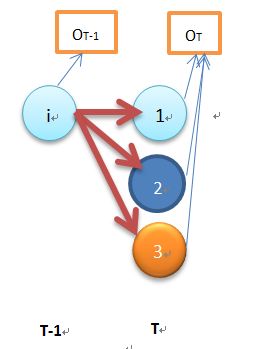
上图是当t=T-1时的状态，

βT-1(i)=P(OT|qT-1=i,λ)=ai1b1(OT)βT(1)+ai2b2(OT)βT(2)+ai3b3(OT)βT(3)

......

当t=1时，

β1(1)=P(O2O3...OT|q2=1,λ)=a11b1(O2)β2(1)+a12b2(O2)β2(2)+a13b3(O2)β2(3)

β1(2)=P(O2O3...OT|q2=2,λ)=a21b1(O2)β2(1)+a22b2(O2)β2(2)+a23b3(O2)β2(3)

β1(3)=P(O2O3...OT|q2=3,λ)=a31b1(O2)β2(1)+a32b2(O2)β2(2)+a33b3(O2)β2(3)

终止条件下：

P(O1O2...OT|λ)=π1b1(O1)β1(1)+π2b2(O1)β1(2)+π3b3(O1)β1(3)

 

程序例证

   

• 后向算法计算P(O|M)：

step1:β4(1) = 1，β4(2) = 1 ，β4(3) = 1

step2:β3(1)=β4(1)a11b1(white)+β4(2)a12b2(white)+β4(3)a13b3(white)              

...

step3:P(O|M)=π1β1(1)b1(O1)+π2β1(2)b2(O1)+π3β1(3)b3(O1)

后向算法示例代码参考下面链接：

http://blog.csdn.net/u011930705/article/details/77373303

1. Viterbi算法

• 介绍:Viterbi算法实际上是用动态规划解HMM预测问题,求概率最大路径

也就是求观察序列的最可能的标注序列

• 问题：给定观察值序列O=o1,…,oT以及一个模型λ=(π,A,B ) 时，如何确定最佳状态序列Q*=q1*,q2* ,…,qT*

• 定义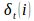： 为时刻t沿一条路径q1,q2,…qt 且qt=i,产生序列O的最大概率

• 求取最佳序列Q*的过程如下：

• 下面解释这个算法：

其中 指的是：从t-1时刻所有单个状态路径到达时刻t状态为j的路径最大概率值。

指的是： t时刻状态为j的所有路径中标记概率最大的第t-1个结点

程序例证

• 计算方法

step1 初始化：δ1(1)=0.2*0.5=0.1，δ1(2)=0.4*0.4=0.16，

δ1(3) = 0.4*0.7=0.28

step2 递推：δ2(1) =max[0.1*0.5,0.16*0.3,0.28*0.2]*0.6

记录ψ2(1)=3 来记录到这个状态的前一个最大可能状态。

...

step3 终结：最佳路径是δ4(1)δ4(2)δ4(3)最大的一个对应的状态

step4 回溯：从最后一个状态往回查找路径

示例代码参考下面链接：

http://blog.csdn.net/u011930705/article/details/77448330

1. EM算法

• 最大期望算法（Expectation Maximization Algorithm，又译期望最大化算法）是一种迭代算法, 用于含有隐变量（hidden variable）的概率参数模型的最大似然估计或极大后验概率估计。

• 算法流程:

Step1:计算期望（E），利用概率模型参数的现有估计值，计算隐藏变量的期望，即求Q函数。

Step2:求极大值（M），利用E 步上求得的隐藏变量的期望，对参数模型进行最大似然估计， 。

终止条件：反复迭代这两步，直至收敛为止。

• Q函数:完全数据的对数似然函数logP(O,Q|λ)关于在给定观测数据O和当前参数λ(i)下对为未观测数据Q的条件概率分布P(Q|O,λ(i))的期望成为Q函数，即 。

。

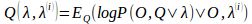举例说明：

假设现在有两枚硬币1和2，,随机抛掷后正面朝上概率分别为P1，P2。为了估计这两个概率，做实验，每次取一枚硬币，连掷5下，记录下结果，如下：

硬币	结果	统计
1	正正反正反	3正-2反
2	反反正正反	2正-3反
1	正反反反反	1正-4反
2	正反反正正	3正-2反
1	反正正反反	2正-3反

可以很容易地估计出P1和P2，如下：

P1 = （3+1+2）/ 15 = 0.4
P2= （2+3）/10 = 0.5

还是上面的问题，现在我们抹去每轮投掷时使用的硬币标记，如下：

硬币 结果 统计

Unknown 正正反正反 3正-2反

Unknown 反反正正反 2正-3反

Unknown 正反反反反 1正-4反

Unknown 正反反正正 3正-2反

Unknown 反正正反反 2正-3反

使用EM算法：

先随便给P1和P2赋一个值，比如：

P1 = 0.2

P2 = 0.7

第一轮抛掷最可能是哪个硬币。

如果是硬币1，得出3正2反的概率为 0.2*0.2*0.2*0.8*0.8 = 0.00512

如果是硬币2，得出3正2反的概率为0.7*0.7*0.7*0.3*0.3=0.03087

然后依次求出其他4轮中的相应概率。做成表格如下：

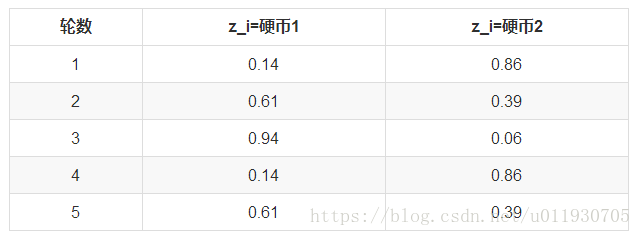
利用上面这个表，我们可以算出每轮抛掷中使用硬币1或者使用硬币2的概率。比如第1轮，使用硬币1的概率是：

0.00512/(0.00512+0.03087)=0.14

使用硬币2的概率是1-0.14=0.86

依次可以算出其他4轮的概率，如下：

这一步，我们实际上是估计出了z的概率分布，这步被称作E步。

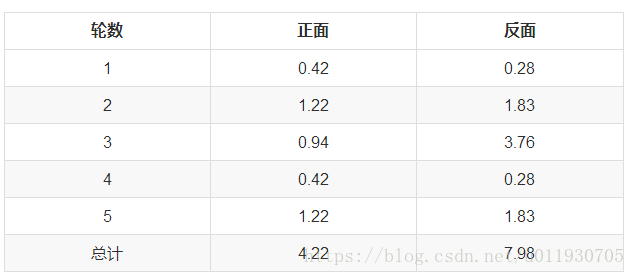
我们按照期望最大似然概率的法则来估计新的P1和P2：

以P1估计为例，第1轮的3正2反相当于

0.14*3=0.42正

0.14*2=0.28反

依次算出其他四轮，列表如下：

P1=4.22/(4.22+7.98)=0.35

可以看到，改变了z值的估计方法后，新估计出的P1要更加接近0.4。原因就是我们使用了所有抛掷的数据，而不是之前只使用了部分的数据。

这步中，我们根据E步中求出的z的概率分布，依据最大似然概率法则去估计P1和P2，被称作M步。

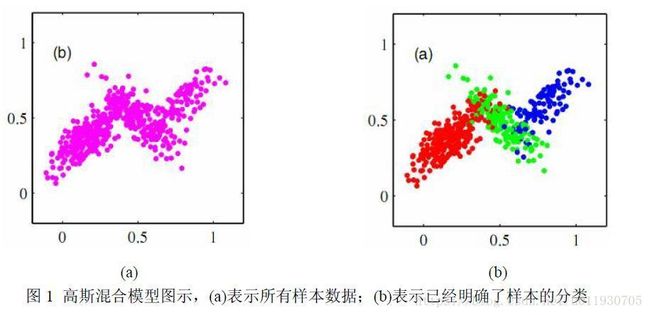
1. 高斯混合模型GMM(几个高斯的叠加)

• 定义：高斯混合模型指具有如下形式的概率分布模型:

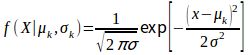其中 是系数，且 , ; 是高斯分布密度是第K个分模型，其中 ， 其中 中的参数可以用EM算法估计,k的取值越大函数拟合的效果越好。

• 在HMM中每个状态都是一个高斯混合分布，所有状态的观察概率密度函数共同构成了HMM模型的参数B。通过MFCC（梅尔频率倒谱系数）进行音素的特征提取，是一个39维特征。语音识别中，一个词由多个音素组成，一个音素对应多个状态。

• 用EM算法可以估计高斯混合模型参数：

其中观测数据是 ,隐含参数是选择第几个模型 j=1,2,…,N;k=1,2,…,T

E步:当前模型参数下第j个观测数据来自第k个分模型的概率

M步：计算新一轮迭代模型参数

重复EM步骤训练参数，直至收敛

• 下图是3个分量系数的高斯混合模型。

1. Baum-Welch算法（非监督学习方法，EM的特例）

• 给定观察值序列O=（o1 o2 … oT）假设一个 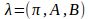，其中隐数据为Y=（y1 y2 … yT）使P(O|λ)最大，通过EM算法训练λ参数。

，其中

• 定义 ：是给定模型λ和观测数据O，在时刻t处于状态qi的概率，记 为

• 在观测O下状态i出现的期望值

• 在观测O下状态i转移的期望值为

其中 推导过程如下：

由后向定义

并假设从T-1开始递推有：

由前向定义

整理得：

以此类推可以推出：

因此可以推出该公式：

• 定义 ：是给定模型λ和观测数据O，在时刻t处于状态qi且在时刻 t+1处于状态qj的概率，记为

• 在观测O下状态i转移到状态j的期望值为

其中 推导过程如下：

所以

因此：

• Baum-Welch算法流程：

Step1：初始化，假设一个模型

Step2：E步，求 和

Step3：M步，利用E步的数据重新计算模型 参数

Step4：反复迭代2,3步直至模型收敛。

1. 基于最大互信息的HMM

• Baum-Wekch算法实际是HMM的最大似然参数估计方法，即给定训练序列O使得P(O|λ)最大，对初始模型的选定要求和经验比较高；而最大互信息估计在此方面优于最大似然估计，但是最大互信息没有前向后向算法那样有效的方法计算，一般只能通过最大梯度法求解。

• 对于训练序列O和模型λ，互信息的定义为：

 

1. 大词汇连续语音识别

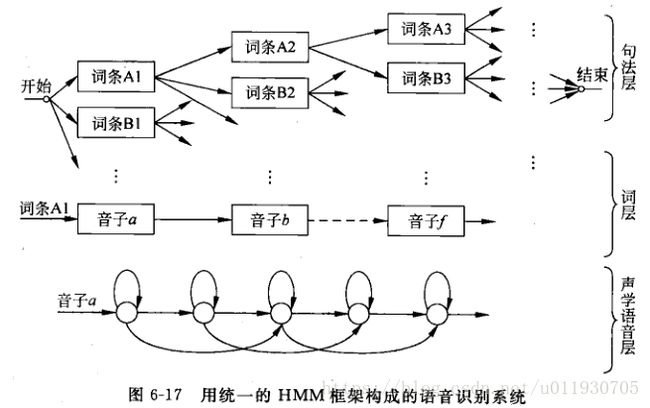
• 通过将声学的语音层、词层、句法层三层引入HMM框架中

1. 声学语音层：是识别系统的底层，接收输入语音，并以一种“子词(subword)”为单位作为识别输出，每个子词单位对应一套HMM结构和参数。

2. 词层：需要一部字典规定词汇表中每个词是由什么音素-音子串接而成。

3. 句法层：规定词按照什么规则组合成句子。句中的一个要选择的词条以一定的概率出现，而选择第二个词条概率与前一个词条有关，以此类推

4. 下图描述了一个统一的HMM框架系统组成图，从状态出发可以逐层扩大到音子，词，句子。

 

 

 

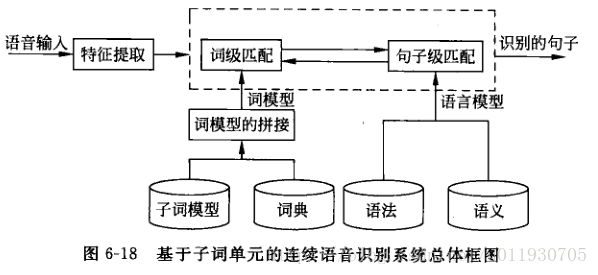
• 大词量连续语音识别总体框架如下图

• 声学模型(语音识别系统底层)：设计一套HMM子词单元模型。

1. 基本声学单元的选择：

1. 英语一般选择音素。

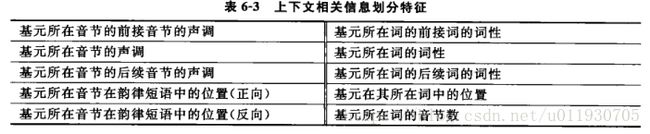
2. 汉语选择声韵母：汉语是单音节，汉语的音节是声韵结构，而且与声母相连的只有韵母或者静音，与韵母相连的也只有声母或者静音，该规则会大大减少上下文相关的声韵母基元数量。

1. 基元的扩展

1. 单纯的声母韵母的音素成为上下文无关的音素，简称单因素。

2. 与左或右相邻音素的相关情况选取的基元，称为双音素。

3. 与左和右同时相关的称为三音素。

解决训练数据稀疏的问题，一般对上下文相关的音素进行聚类并根据聚类进行状态共享。有两种方法。

1. 基于数据驱动状态共享策略（不能处理无样本音素）

HTK（HMM tools kit）提供了一种基于最小类合并的 数据驱动聚类方法。

1. 基于决策树状态共享策略

 

 

 

 

 

 

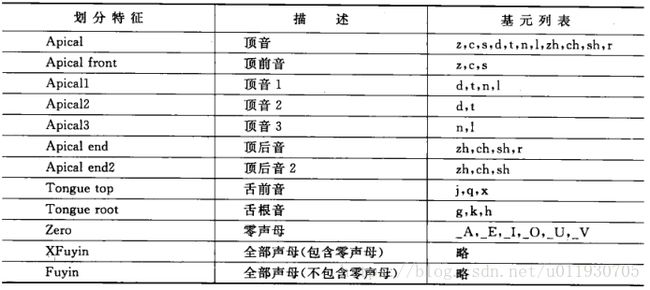
a.发音相似性：包括韵母划分特征、声母划分特征

b.基元的上下文相关信息

c.ID3决策树算法：从根结点开始，对结点计算所有可能特征问题的信息增益，选择信息增益最大的特征作为结点的特征，由该特征的不同取值建立子结点，再对子结点递归调用以上的方法。

随机变量熵定义：

Info（D）=

信息增益公式：

Gain（A）=Info（D)-Info（D|A）

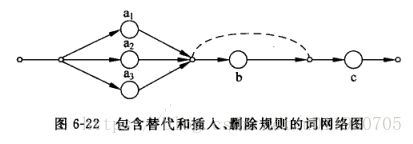
1. 声学-语音学层之间的词层字典用网络图来描述（每个词由哪些子词以何种方式组合）

1. 声调处理：有一种方法可以将韵母细化从而回避此问题。

1. 基于子词单元的HMM训练

一般采用从左到右的结构，状态数固定2-4个。每个语音段中包含多个子词单元，因为一个足够大的训练集每个子词单元都可以出现很多次。

使用分段K均值算法产生最佳模型：

1. 初始化：将每个训练语句线性分割成子词单元，将每个子词单元线性分割成状态。（每个语句子词单元和内部状态驻留时间是均匀的）

2. 聚类：每个给定子词单元的每个状态，在所有训练语句段中用特征矢量用k均值算法聚类。

3. 参数估计：根据聚类结果计算均值，各维方差和混合权值系数。(GMM)

4. 分段：根据上一步得到的新的子词单元模型通过viterbi算法对所有训练语句再分成子词单元和状态，重新迭代聚类和参数估计，直到收敛。

 

 

 

 

1. 其他语音相关

• HMM孤立词识别过程：

1. 首先通过HMM训练算法（Baum-Welch）为系统词汇表的每个词建立对应的模型λi。

2. 然后通过前向后向算法或Viterbi算法求出哥哥概率P(O|λi)值，其中O为待观察值的观察值序列。

3. 最后在后处理阶段，选取最大的概率值所对应的词为O的识别结果。

• 在孤立词语音识别中，最为简单有效的方法是采用DTW(Dynamic Time Warping，动态时间归整)算法，该算法基于动态规划(DP)的思想，解决了发音长短不一的模板匹配问题，是语音识别中出现较早、较为经典的一种算法，用于孤立词识别。HMM算法在训练阶段需要提供大量的语音数据，通过反复计算才能得到模型参数，而DTW算法的训练中几乎不需要额外的计算。所以在孤立词语音识别中，DTW算法仍然得到广泛的应用。

• 连接词识别（穷举法很难实现）动态规划。