An Introduction to Conditional Random Fields[条件随机场介绍]
An Introduction to Conditional Random Fields
By Charles Suttonand Andrew McCallum
文献网址:http://homepages.inf.ed.ac.uk/csutton/publications/crftut-fnt.pdf
[译]条件随机场介绍
By wttttt
2.Modeling建模
本节我们从建模的角度描述CRFs,解释一个条件随机场是如何将结构化输出的分布表示成一个高维输入向量的函数的。CRFs可以被理解成logistic回归分类器到任意图形结构的一种扩展,或者理解成结构化数据的生成模型的判别模拟,比如说隐马尔科夫模型(生成模型)。
我们首先对图模型做一个简要的介绍(2.1节),接着描述NLP(自然语言处理)中的生成和判别模型(2.2节)。然后我们将呈现条件随机场的正式定义,既包括常用的线性链案例(2.3节),也包括通用图结构(2.4节)。由于一个条件随机场的精度强烈地依赖于所使用的特征,因此我们也描述一些用于工程特征的常用技巧(2.5节)。最后,我们介绍CRFs的两个应用示例(2.6节),以及关于CRFs的典型应用领域的一个更广阔的调研。
2.1图形建模
图模型是用于多变量概率分布的一个有力的表示和推断框架。它已经在多个随机建模领域被证明是有效的,包括编程理论,计算机视觉,知识表示,贝叶斯统计以及自然语言处理。
多变量分布的表示是昂贵的。举例来说,n个二进制变量的联合概率表需要O(2^n)级别的浮点数存储。图形建模观点的视角是多变量的分布常常可以被表示为局部函数的乘积,每个局部函数取决于一个更小的变量子集。这种因式分解结果是与变量之间确定的条件依赖关系有了紧密的连接—两种类型的信息都容易地被概括成一个图。确实,这种因式分解之间的关系,条件依赖,以及图结构几乎构成了大部分的图形建模框架:条件依赖的视角对模型设计是最有用的,因式分解的视角对推论算法设计是最有用的。
本节接下来的部分,我们将从因式分解和条件依赖的角度介绍图模型,主要关注基于无向图模型。一个更细节的现代图形建模方法以及精确地推论可以参考Koller和Friedman的著作。
2.1.1无向图
我们考虑随机变量集合Y的概率分布。我们通过整数s∈1,2,…,|Y| 索引这些变量。每个Ys∈Y来自集合Y,Ys可以是连续或离散的,尽管我们在这次研究中仅考虑离散的情况。Y的一个随机赋值表示为向量y。给定一个变量Ys∈Y,符号ys表示y内分配给Ys的值。记号1{y=y’}表示y的指示函数,当y=y’时取值为1,否则取值0。我们还需要边缘化符号。对于一个给定的变量赋值ys,我们使用和∑y\ys来表示所有可能的赋值y的和,其中y对于变量Ys的值是ys。
假设我们相信一个概率分布p可以被表示成ψa(ya)形式的因子的乘积,其中a是1到A范围的整数索引。每一个因子ψa仅取决于变量子集Ya⊆Y。ψa(ya)是一个非负标量,它可以被认为是ya之间的兼容度量值。有高兼容性的值之间将有更高的概率。因式分解可以允许我们更有效地表示p,因为集合Ya可能比全变量集Y小很多。
一个无向图模型是概率分布的家庭,根据每个给定的因子集合进行因式分解。正式地,给定一个Y的子集集合{Ya}(a=1 to A),一个无向图模型是所有分布的集合,它可以被写作
对于任意选择的因子F = {Ψa},其对所有的ya有Ψa(ya)≥0。(因子也被称为局部函数或兼容性函数。)我们将使用术语随机场来通过一个无向图模型来定义的一个特别的分布。
常量Z是归一化因子,为了保证分布p的和为1.它被定义为
Z被认为是因子集合的函数,它也被称为配分函数(译者注:partition function)。注意到(2.2)的求和式是基于指数级别的y的可能赋值。由于这个原因,Z的计算通常是棘手的,但是很多现有的工作是关于如何估计它的(参见第4节)。
术语“图模型”的由来是因式分解(2.1)可以利用图来简洁地表示。一个非常自然地形式是通过因子图(译者注:factor graphs)。一个因子图是一个双向图G=(V, F, E),图中一个点集V={1,2,…,|Y| }指示模型的随机变量,图中其它点集F={1,2,…A}指示因子。图的语义学是,如果一个变量点Ys(s∈V)与一个因子点Ψa(a∈F)相连,那么Ys是Ψa的一个参数(译者注:argument)。因此一个因子图直接地描述了一个分布p是如何分解成局部函数的乘积的。
我们正式地定义这个概念--一个因子图是否“描述”了一个给定的分布。用N(a)表示索引为a的因子的邻居。那么:
定义2.1 如果存在因子图G的一个局部函数集合Ψa以至于p可以写作如下形式,那么分布p(y)可依据G进行分解
一个因子图G以同样的方式描述一个无向图模型。在(2.1),使用子集集合作为邻居集合s {YN(a)|∀a ∈ F}。从定义(2.1)导出的无向图模型就是根据图G因式分解得到的分布集合。
举例来说,图2.1显示了一个有三个随机变量的因子图的例子。图中,圆圈是变量点,阴影框是因子点。我们已经根据变量和因子的索引为点贴上了标签。这个因子图描述了三个变量的所有的分布p的集合,它可以变写作p(y1,y2,y3)=Ψ1(y1,y2)Ψ2(y2,y3)Ψ3(y1,y3),对所有的y = (y1,y2,y3)。
图模型的因式分解和变量之间的条件依赖之间存在紧密的联系。这种联系可以通过一个被称作马尔科夫网络的不同的无向图来理解,马尔科夫网络直接地表示了多变量分布中的条件依赖关系。马尔科夫网络仅仅基于随机变量,而非随机变量和因子。用G表示一个无向图,其顶点V={1,2,…,|Y|}索引每一个随机变量。对于一个变量索引s∈V,用N(s)表示它在G中的邻居。如果分布p满足局部马尔可夫特性,那么我们说p是关于G的马尔科夫。局部马尔可夫性:对任意两个变量Ys, Yt ∈Y,变量Ys在它的邻居YN(s)下条件独立于Yt。直觉地,这意味着YN(s)本身包含了预测Ys所需的所有有用信息。
按照(2.1)给定一个分布p的因式分解,一个相应的马尔科夫网络可以通过连接所有共享同一个局部函数的变量对来构建。
一个马尔科夫网络从因式分解的角度来看是由不良的歧义的。考虑如图2.2(左)所示的三节点马尔科夫网络。任意的分布因式分解成p(y1,y2,y3) ∝f(y1,y2,y3),f为正函数,对于该图就是马尔可夫的。然而,我们可能希望使用一个更严格的参数化形式,即p(y1,y2,y3) ∝ f(y1,y2)g(y2,y3)h(y1,y3)。图中的第二种模型家族是第一种的严格子集,因此在这个更小的家族里我们可能不需要那么多的数据来精确地估计分布。但是马尔可夫网络形式不能够分辨这两种参数化形式。相比之下,因子图更准确地描述了因式分解。
2.1.2 有向图
无向模型中的局部函数不需要直接地概率解释,一个有向概率模型描述一个分布是如何因式分解成局部条件概率分布的。G是一个有向无环图,其中π(s)是G中的Ys双亲[译者注:parents]的索引。一个有向图模型是一个分布家族,它可以被分解为:
我们将分布p(ys|yπ(s))作为局部条件分布。注意π(s)对没有双亲的变量可以是空的。在这种情况下p(ys|yπ(s))可以被理解成p(ys)。
可以通过感应来表示p被正确地归一化。有向模型可以被认为是一种因子图,图中个体因子都通过特殊方式被局部归一化了,以至于因子等于变量子集下的条件分布,并且归一化变量Z=1。有向模型经常被用作生成模型,我们将会在2.2.3节解释。一个有向模型的例子是朴素贝叶斯模型(2.7)。
2.1.3 输入和输出
该研究考虑我们预先知道要预测的变量的场景。模型中的变量将会被划分成输入变量X的集合,X我们假设总是可观测的,另一个是输出变量的集合Y,Y是我们希望预测的。例如,一个赋值x可能表示句子中所出现的每个单词的向量,y表示每个单词的语音标签向量。
我们队构建变量X∪Y的联合分布感兴趣,我们将扩展之前的标号来适应这个。例如,基于X和Y的无向模型:
其中每个局部函数Ψa取决于两个变量子集Xa ⊆ X 以及 Ya ⊆ Y。归一化常量变成
其中包括了所有x,y取值的和。
2.2 生成模型Vs判别模型
本节我们讨论一些已用于自然语言处理的简单图模型的例子。尽管这些例子已经广为人知,它们仍然可以使上一节的定义清楚化,并且阐述一些我们将会再次在CRFs的讨论中提及的一些想法。我们会特别关注隐马尔科夫模型,因为它与线性链条件随机场关系密切。
本节的主要目的之一是比较生成模型和判别模型。我们将要讨论的模型中,两个是生成模型(朴素贝叶斯和HMM),一个是判别模型(logistic回归)。生成模型是描述一个标签向量y如何概率的“生成“特征向量x的模型。判别模型致力于相反的方向,直接地描述如何对一个特征向量x赋予标签y。原理上,使用贝叶斯准则,每一种类型的模型都可以被转化为其他类型,但是实际上这些方法是有区别的,正如我们将在2.2.3节讨论的,每一种都有潜在的优点。
2.2.1 分类
首先我们讨论分类问题,也即,给定特征x=(x1,x2,...,xK),预测一个单一离散类别y。一个简单地实现方法是假设一旦标签类别已知,所有的特征是独立的。这样得到的分类器称作朴素贝叶斯分类器。它是基于联合概率模型:
该模型可以通过有向图来描述,如图2.3(左)。我们也可以将这个模型写作因子图的形式,通过定义Ψ(y) = p(y),对每个特征xk定义因子Ψk(y,xk) = p(xk|y)。该因子图如图2.3(右)。
另一种著名的被自然地表示成图模型的分类器是logistic回归(有时在NLP社区被称作最大熵分类器)。该分类器是出于每个类的对数概率logp(y|x)是x的线性函数加上一个归一化常数的假设。这形成了条件分布:
其中 是归一化常数项,θy是偏差权重,就像朴素贝叶斯中的logp(y)。不同于对每个类使用一个权重向量,如(2.8)所示,我们可以使用一个不同的记号,其中权重的单一集合可以在所有类别中共享。诀窍就是定义一个只对单一类非零的特征函数集合。为了做到这个,特征函数可以被定义为作为特征权重,作为偏差权重。现在我们可以使用fk来索引每个特征函数,使用θk来索引其相应的权重。使用这种记号技巧,logistic回归模型变成了:
我们引入这种记号因为它反射了我们将会呈现的CRFs的记号。
2.2.2 序列模型
分类器仅仅预测一个单一类变量,但是图模型的真正力量在于它们建模多个互相关变量的能力。本节,我们讨论依赖的最简单形式,其中图模型的输出变量按序列排序。为了诱发这个模型,我们讨论自然语言处理中的一个模型,命名实体识别(NER)任务。NER是个辨认和分类文本中的正确名字的问题,名字包括位置,比如中国;任命,比如乔治;以及组织,比如联合国等。命名实体识别任务是给定一个句子,分割实体词语,并将其按类别分类。该问题的挑战在于,许多命名实体字符串出现频率太低,甚至在一个巨大的训练集中,因此系统必须基于上下文来识别它。
NER的一个方法是独立分类每一个词作为人名、位置、组织或其他(意味着不是一个实体)中的一个。该方法的问题是它假定对给定输入,所有的命名实体都是独立的。事实上,相邻单词的命名实体标签是相互依赖的;例如,New York是一个位置,而New York Times是一个组织。放松这种独立假设的一个方法是将输出变量组织成一个线性链。这就是隐马尔可夫模型所使用的方法。HMM通过假定存在一个隐藏状态序列来建模一个观测序列。令S为有限的可能状态,O为优先的可能观测,也即,对所有的t 有xt ∈ O 及yt ∈ S。
为了建模联合分布p(y,x),HMM做了两个独立假设。第一,它假设每一个状态仅仅依赖于它当前的前身(immediate predecessor),也即每一个状态yt在给定yt-1的情况下与y1,y2,…,yt-2独立。第二,它还假设每一个观测变量xt仅取决于当前状态yt。基于这些假设,我们可以使用三个概率分布详述HMM
为了简化上述等式中的记号,我们创建一个“仿制”初始状态y0。这允许我们将初始分布p(y1)写作p(y1|y0)。
HMM已经被用于许多自然语言处理中的额序列标签任务中了,比如词性标注,命名实体识别以及信息提取。
2.2.3 比较
生成模型和判别模型都描述了(y,x)上的分布, 但是它们致力于不同的方向。生成模型,比如朴素贝叶斯分类器和HMM,是联合分布的家族,可以被分解成p(y,x) = p(y)p(x|y),也即它描述了给定标签,如何采样,或“生成”特征值。判别模型,比如logistic回归模型,是条件分布p(y|x)的家族,也即分类规则被直接建模。原则上,判别模型也可以被用来获取联合分布p(y,x),通过提供一个边缘分布p(x),但这很少需要。
生成和判别模型主要的概念不同在于条件分布p(y|x)不包括p(x)的模型,其对分类而言是不需要的。建模P(x)的困难在于它常常含有高依赖性的难以建模的特征。比如,在名称实体识别中,一个朴素的HMM的应用仅依赖于一个特征。但是很多词语,尤其是正确地名称将不会出现在训练集中,因此词身份特征是没有信息量的。为了标注不可见的词语,我们将利用词的其他特征,比如它的资本化、邻居词语、前缀、后缀等。
判别模型的主要优点是它更适用于丰富的、交叠的特征。为了理解这个,考虑朴素贝叶斯分布家族(2.7)。这是一个联合分布的家族,其中的条件均具有“logistic回归形式”(2.9)。但是存在许多其他联合模型,一些x之间有复杂的依赖关系,它们的条件分布仍然具有(2.9)的形式。通过直接建模条件分布,我们可以保留对p(x)形式的不可知。判别模型,例如CRFs,做了y之间条件独立的假设,以及y如何依赖于x的假设,但是没有对x之间的条件独立性做假设。这个观点可以通过图来理解。假设我们有一个因子图代表联合分布P(y,x)。如果我们接着构造一个条件分布p(y|x)图,任何仅依赖于x的因子从图结构中消失。它们是条件不相关的,因为它们是关于y的常数。
为了概括生成模型中特征的互相关性,我们有两个选择。第一个选择使增强模型来表示输入之间的相关性,比如通过加入每个xt之间的有向边。但是这通常是很难实现。例如,很难想象如何对词的大写和词的后缀之间建模,我们也特别不希望这么做,因为我们总是观察测试句子。
第二个选择是简化互相关性假设,比如朴素贝叶斯假设。例如,带有朴素贝叶斯假设的HMM模型将会有p(x,y) =的形式。这种想法有时会很有效。但是它也可能有问题,因为独立性假设会影响性能。例如,尽管朴素贝叶斯分类器在文档分类上表现很好,但是它在很多应用上性能平均比logistic回归要差。
并且,朴素贝叶斯会产生差的概率估计。作为一个解释性的例子,设想在两个特征重复的分类问题上训练朴素贝叶斯,也即,给定一个原始特征向量x=(x1, x2,…xk),我们将其转化为x’=(x1,x1,x2,x2,…xk,xk),然后运朴素贝叶斯。尽管数据集中没有添加新的信息,这个转化会增加概率估计的信心,通过这个朴素贝叶斯对于p(y|x’)的估计比起p(y|x)会远离0.5。
当我们生成序列模型时,类似朴素贝叶斯的假设变得尤其有问题,因为推论会合并模型不同部分的证据。如果每个序列位置的标签概率估计都是自信的,那么合理地合并它们将是困难的。
朴素贝叶斯和logistic回归之间的不同仅仅在于第一个是生成模型而第二个是判别模型;这两个分类器对离散输入在所有其他方面都是一样的。朴素贝叶斯和logistic回归考虑同一个假设空间,因此任意logistic回归可以转换成一个有相同决策边界的朴素贝叶斯分类器,反之亦然。另一个说法是朴素贝叶斯模型(2.7)与logistic回归模型(2.9)定义了相同的分布家族,我们可以这样阐述:
这意味着如果朴素贝叶斯模型(2.7)依据最大条件似然来训练,我们将会得到和logistic回归一样的分类器。相反,如果logistic回归模型生成地解释成(2.11)的形式,并且通过联合似然p(y,x)最大化来训练,那么我们将得到和不铺贝叶斯一样的分类器。在Ng andJordan[98]的术语中,朴素贝叶斯和logistic回归组成了一个生成-判别对。一个近期的生成和判别模型的理论视角,可以参考Liang and Jordan [72]。
原则上,为什么这些方法如此不同可能是不清晰的,因为我们总是可以使用贝叶斯准则来在这两种方法之间转换。例如,在朴素贝叶斯模型中,很容易将联合p(y)p(x|y) 转换成条件分布p(y|x)。确实,这种条件和logistic回归有一样的形式(2.9)。并且如果我们设法为数据获得一个“真正的”生成模型,也即从实际采样的数据中获取分布p*(y,x)=p*(y)p*(x|y),然后我们应该简化p*(y|x)的计算,这实际上是判别方法的目标。但这是严格的,因为我们从未拥有这两种方法在实际中不同的真实分布。首先估计p(y)p(x|y),然后计算直接结果P(y|x)。换句话说,生成和判别模型都有着估计p(y|x)的目标,但是它们采取了不同的方法。
一种洞察了生成和判别建模的不同的观点是由于Minka[93]。假设我们有一个生成模型pg,参数θ。根据定义,它有这样的形式:
但是我们可以使用概率的链规则将将pg重写成:
现在,我们将该生成模型与联合概率家族上的一个判别模型进行比较。为了达到这个目的,我们定义一个输入的先验p(x),这样p(x)可以从通过一些参数设置从pg中产生。也即,。那么结果分布是:
通过对比(2.13)和(2.14),我们发现条件方法能更自由的拟合数据,因为他不需要θ= θ’。直觉上,由于(2.13)中的参数θ在输入分布和条件分布中都使用了。
机关到目前为止我们都在批判生成模型,但是他们确实有其优点。首先,生成模型可以更自然地处理潜在变量,部分标记数据以及未标记数据。在很多极端的例子中,当数据完全为标记,生成模型就可以被用在非监督模式中,然而非监督学习在判别模型中是不自然的,它仍处于研究活跃期。
第二,在某些例子中生成模型会比判别模型表现更好,直觉上是因为输入模型p(x)可能在条件上有一个平滑的影响。Ng和Jordan[98]证明了这种影响在数据集很小的时候是尤其显著的。对于许多特别的数据集,预测生成模型和判别模型谁的性能更好是不可能的。最后,有时要么问题暗示了一个自然的生成模型,或应用需要预测未来输出和输入的能力,这些都使得生成模型更可取。
因为生成模型有着p(x,y)=p(y)p(x|y)的形式,它经常很自然的通过有向图来表示,该有向图中输出y拓扑地先于输入。类似地,我们会看到通过无向图能更自然地表示判别模型。然而,并不总是符合上述情况,有无向生成模型,如Markov随机场(2.32),有向判别模型,如MEMM(6.2)。
朴素贝叶斯回归和logistics回归之间的关系反应了HMMs和线性链CRFs之间的关系。正如朴素贝叶斯和logistics回归是生成-判别对一样,HMM的判别的相似物为CRF的部分特别案例,这是我们下一节会讲到的。它们四者之间的相似性关系展现在图2.4中。
参考文献:
【98】A. Y. Ng and M. I. Jordan, “Ondiscriminative vs. generative classifiers:
A comparison of logistic regression and naive Bayes,” inAdvances in Neural
Information Processing Systems 14, (T. G. Dietterich, S. Becker,and
Z. Ghahramani, eds.), pp. 841–848, Cambridge, MA: MIT Press,2002
【72】P. Liang and M. I. Jordan, “An asymptoticanalysis of generative, discriminative,
and pseudolikelihood estimators,” in International Conference on
Machine Learning (ICML), pp. 584–591, 2008.
【93】T. P. Minka, “Discriminative models, notdiscriminative training,” Technical
Report MSR-TR-2005-144, Microsoft Research, October 2005.
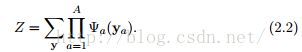
![An Introduction to Conditional Random Fields[条件随机场介绍]_第1张图片](http://img.e-com-net.com/image/info8/b440be18d8df450c8830f940504affae.jpg)
![An Introduction to Conditional Random Fields[条件随机场介绍]_第2张图片](http://img.e-com-net.com/image/info8/b5ba92fdb13d4b9eb3200f5ac8e0a6d3.jpg)
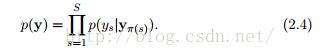
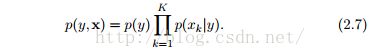
![An Introduction to Conditional Random Fields[条件随机场介绍]_第3张图片](http://img.e-com-net.com/image/info8/1c16e58e50844305b3f4d9ce6eb9f7cd.jpg)



![An Introduction to Conditional Random Fields[条件随机场介绍]_第4张图片](http://img.e-com-net.com/image/info8/d6cf229677d644fd82074728f785429f.jpg)