[SIGIR‘20] Certifiable Robustness to Discrete Adversarial Perturbations for Factorization Machines
FM对离散对抗扰动的可信鲁棒性
![[SIGIR‘20] Certifiable Robustness to Discrete Adversarial Perturbations for Factorization Machines_第1张图片](http://img.e-com-net.com/image/info8/daf6c2d77ce34344905a6396e92febcb.jpg)
现有的健壮性训练方法忽略了离散特征,并且缺少有效的检验机制。本文首次进行了FM对离散对抗扰动的鲁棒性研究。
Motivation
核心的想法是通过训练让真实的样本更可信,让扰动影响的样例最少。
在一个确定的扰动空间中(比如可变特征数是最大维度),生成离散的worst-case。在worst-case下的模型依旧健壮,足以证明模型在一般情况下的鲁棒性。
Related Works
现有的鲁棒FM考虑用户信号上的环境噪声,仅仅在这样的噪声上建模(如 ϵ ∈ N ( μ , σ 2 ) \epsilon \in \mathcal{N}(\mu, \sigma^2) ϵ∈N(μ,σ2)),然后通过最小化最糟糕情况的损失寻找对于所有可能扰动的可行解。
这样的办法
- 假设扰动服从连续分布,忽略了离散特征,不适合FM。比如认为的是[0, 0.05]一个小区间之间的值,实际上可能是{1, -1},有或者没有。
- 缺少有效的检验机制。现有的工作比较特定噪声下的模型性能,不适合较大的扰动空间。
时间复杂度和扰动敏感性是两大挑战。
Model
Is it robust?
![[SIGIR‘20] Certifiable Robustness to Discrete Adversarial Perturbations for Factorization Machines_第2张图片](http://img.e-com-net.com/image/info8/5b3172953c6743b3adfa630a65c2d053.jpg)
FM的预测值:
![[SIGIR‘20] Certifiable Robustness to Discrete Adversarial Perturbations for Factorization Machines_第3张图片](http://img.e-com-net.com/image/info8/2552e0d23f234706b387f5c23ef5f643.jpg)
和10年Rendle论文的区别在于,j从1开始,因此计算后是+
![[SIGIR‘20] Certifiable Robustness to Discrete Adversarial Perturbations for Factorization Machines_第4张图片](http://img.e-com-net.com/image/info8/39aef4943fe7413a92bcaba74aad46c3.jpg)
假定负类正类标签 {-1, 1}
加入扰动后,预测的差值定义为:
δ = f θ ( x ^ ) − f θ ( x ) \delta = f_\theta(\hat{x}) - f_\theta(x) δ=fθ(x^)−fθ(x)
只要 f θ ( x ) + δ f_\theta(x) + \delta fθ(x)+δ不变号,说明预测依然正确。
如果计算所有的这样的delta,计算代价会非常大。与之前的假设相同,计算worst-case的情况,即 f > 0 f>0 f>0, f θ ( x ) + δ m i n > 0 f_\theta(x) + \delta_{min} > 0 fθ(x)+δmin>0;反之, f θ ( x ) + δ m a x < 0 f_\theta(x) + \delta_{max} < 0 fθ(x)+δmax<0 即可。
记 x ′ ∈ { 0 , 1 } 1 × d x' \in \{0, 1\}^{1×d} x′∈{0,1}1×d 为扰动向量,只有history部分为1,history长度为 n , n < d n, n
x ^ = x + x ′ \hat{x} = x + x' x^=x+x′
δ \delta δ根据之前的公式求差,实际化简后代表了——
扰动向量一阶加权和 + 输入与干扰量的的联系 + 干扰量自身各个维度的联系
![[SIGIR‘20] Certifiable Robustness to Discrete Adversarial Perturbations for Factorization Machines_第5张图片](http://img.e-com-net.com/image/info8/74fc6e7d2db94d00bcdb3a61de1aa2f6.jpg)
复杂度问题
其中,计算 ∑ f = 1 k ( ∑ j = 1 d v j , f x j ′ ) 2 \sum_{f=1}^k(\sum_{j=1}^dv_{j,f}x'_j)^2 ∑f=1k(∑j=1dvj,fxj′)2中,找到合适的子集使得 δ \delta δ最大或最小是一个NP-C问题(子集势为 q q q 时,暴力求解复杂度为 O ( ∑ i = 1 q C d i ) = O ( d q ) O(\sum_{i=1}^qC_d^i) = O(d^q) O(∑i=1qCdi)=O(dq), q = d q=d q=d 时,为 O ( 2 d ) O(2^d) O(2d))。
非鲁棒验证
这里注意,
Σ f = 1 k ( Σ j = 1 d v j , f x j ′ ) 2 \Sigma_{f=1}^k(\Sigma_{j=1}^d v_{j,f} x_j')^2 Σf=1k(Σj=1dvj,fxj′)2 转换为了 ∑ f = 1 k v j , f 2 \sum_{f=1}^{k}v^{2}_{j,f} ∑f=1kvj,f2
是基于每一步只考虑当前步最大收益的思想。
每次只改变 j j j上的分量为1(其他分量都为0),那么 ∑ v j , f x j ′ \sum v_{j,f}x'_j ∑vj,fxj′ 这一项实际就等于 v j , f v_{j,f} vj,f,
另外,这个公式是每一步都要计算一遍, v i v_i vi 更新了之前步加入的 j j j,和之后robust certificates不同。
每次选择当前最优解的index赋1,预测label改变时中止。
![[SIGIR‘20] Certifiable Robustness to Discrete Adversarial Perturbations for Factorization Machines_第7张图片](http://img.e-com-net.com/image/info8/1f2b6b66d68443648ca3e023d447455e.jpg)
鲁棒验证
对于负(正)类,寻找 δ \delta δ 的上(下)界。公式(5)分为两个子问题计算。为方便讨论,设label=-1:
每个 j j j 产生的影响 p j p_j pj 相互独立,可以直接计算
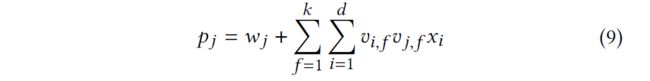
然后选取 q q q 个即可
第二子问题是一个NP-C问题,
首先将二次型展开为:

式(8)等价于
![[SIGIR‘20] Certifiable Robustness to Discrete Adversarial Perturbations for Factorization Machines_第8张图片](http://img.e-com-net.com/image/info8/e093d7d8476d4a47b0c0370172ba5e1b.jpg)
实际上又绕回到了原本的二阶关系上。
可以直接选择前 q ( q + 1 ) 2 \frac{q(q+1)}{2} 2q(q+1) 个,不必考虑 i , j i, j i,j对应是否都为1,只要求出bound的数值就行。
训练
现按照原始损失函数(实际是经过Sigmoid的NLLLoss)训练
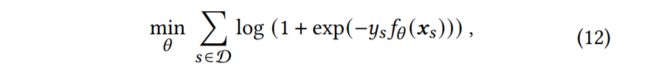
收敛后,修改为

实验
非可信鲁棒对应的实验证明扰动的影响
![[SIGIR‘20] Certifiable Robustness to Discrete Adversarial Perturbations for Factorization Machines_第9张图片](http://img.e-com-net.com/image/info8/fd588bdc6beb485aad9c3d00583e26e3.jpg)
可信鲁棒对应的实验证明,经过FM-RT的模型抗扰动性更好(Avg-max q q q可以更多),但Acc会略有损失。换句话说,FM-RT提高了模型的泛化能力。
![[SIGIR‘20] Certifiable Robustness to Discrete Adversarial Perturbations for Factorization Machines_第10张图片](http://img.e-com-net.com/image/info8/e8efc8a3b5894a78984246b7669dbe52.jpg)
这是我用pytorch复现的版本:FMRT
![[SIGIR‘20] Certifiable Robustness to Discrete Adversarial Perturbations for Factorization Machines_第6张图片](http://img.e-com-net.com/image/info8/f7a69b75afdd4ff2a40399a8f15b18cf.jpg)

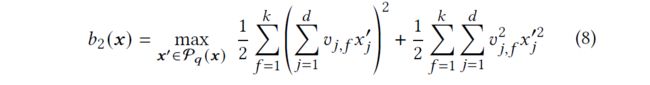
![[SIGIR‘20] Certifiable Robustness to Discrete Adversarial Perturbations for Factorization Machines_第11张图片](http://img.e-com-net.com/image/info8/c3b1de83259c4ac19b0acc5bf78aa4a2.jpg)