逻辑回归

1逻辑回归知识点小结

分类问题的一些例子

• 判断一封电子邮件是否是垃圾邮件
• 判断一次金融交易是否是欺诈
• 判断一个肿瘤是良性还是恶性

假说表示

• 逻辑回归模型的假设是：
  $$h_{\theta }(x)=g\left({\theta }^{T}X\right)$$

X 特征向量
g 逻辑函数sigmoid function

sigmoid function的代码实现：

$$g(z)=\frac{1}{1+e^{-z}}$$

import numpy as np
def sigmoid(z):
    return 1/(1+np.exp(-z))

对回归模型的理解

• 对于给定的输入变量，根据选择的参数计算输出变量为1（正向类）的可能性，即：
  $$h_{\theta }(x)=P(y=1|x;\theta )$$

判定边界

• 逻辑回归：
  $$h_{\theta }(x)=g\left({\theta }^{T}X\right)=P(y=1|x;\theta )$$$$g(x)=1/1+e^{-z}$$

当$h_{\theta }(x)$大于等于0.5时，预测y=1
当$h_{\theta }(x)$小于0.5时，预测y=0

---

上面例子：当-3+x1+x2大于等于0，即x1+x2大于等于3时，模型将预测y=1

代价函数

$J\left(\theta \right)=\frac{1}{m}\sum _{i=1}^m[-y^{(i)}\log \left(h_{\theta }\left(x^{(i)}\right)\right)-\left(1-y^{(i)}\right)\log \left(1-h_{\theta }\left(x^{(i)}\right)\right)]$

• 代码实现：

import numpy as np
def cost(theta,X,y):
    theta=np.matrix(theta)
    X=np.matrix(X)
    y=np.matrix(y)
    first=np.multipy(-y,np.log(sigmoid(X*theta.T)))
    second=np.multipy((1-y),np.log(1-sigmoid(X*theta.T)))
    return np.sum(first-second)/len(X)

简化的成本函数和梯度下降

• 用梯度下降法最小化逻辑回归中的代价函数$J(\theta )$

高级优化

• 共轭梯度法BFGS（变尺度法）、L-BFGS（限制变尺度法）
• 线性搜索算法（linear search）

多类别分类

• 自动归类邮件（1：工作；2：朋友；3：家人）
• 药物诊断（1：没有感冒；2：感冒；3：流感）
• 天气分类问题（1：晴天；2：阴天；3：雪天）

过拟合问题

• 丢弃一些不能帮助正确预测的特征。手工选择保留哪些特征/使用一些模型选择算法来帮忙（PCA）
• 正则化。保留所有的特征，但是减少参数的大小（magnitude）

2 预测某位学生能否被录取

• 数据可视化

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

path = 'ex2data1.txt'
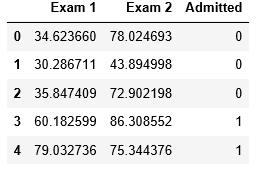
data = pd.read_csv(path, header = None, names = ['Exam 1', 'Exam 2', 'Admitted'])
data.head()#前5组数据

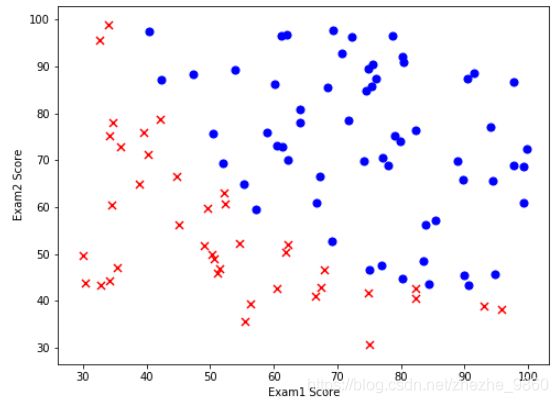
# 绘制散点图
# 紫色圆点 录取
# 红色差号 未录取
positive = data[ data['Admitted'].isin([1]) ]
negative = data[ data['Admitted'].isin([0]) ]

fig,ax = plt.subplots(figsize = (8,6))
ax.scatter(positive['Exam 1'], positive['Exam 2'], s = 50, c = 'b', marker = 'o', label = 'Admitted')
ax.scatter(negative['Exam 1'], negative['Exam 2'], s = 50, c = 'r', marker = 'x', label = 'Not Admitted')
ax.legend
ax.set_xlabel('Exam1 Score')
ax.set_ylabel('Exam2 Score')

• pandas中isin()函数

isin()接收一个列表，判断该列中元素是否在列表中

df = pd.DataFrame( np.random.randn(4,4), columns=['A','B','C','D'] )
df
df.A > 0 #布尔索引
df[ df.A > 0 ] #布尔索引应用

#使用isin()
df['E'] = ['a','a','b','c'] #添加一列E
df['E'].isin(['a', 'b', 'c']) #判断E这一列有没有元素 a b c

df.isin(['a', 'b']) #判断df中有没有 a b
df[ df['E'].isin(['a']) ] #将E列中有元素a的列生成一个新的DataFrame

• 使用逻辑回归,训练模型来预测结果.实现逻辑回归

Sigmoid函数
$g$代表一个常用的逻辑函数，形状为$“S”$形，称$S$形函数
$$g(z)=\frac{1}{1+e^{-z}}$$合起来，得到逻辑回归模型的假设函数
$$h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}X}}$$

def sigmoid(z):
    return 1/(1+np.exp(-z))

• 代价函数
  $J\left(\theta \right)=\frac{1}{m}\sum _{i=1}^m[-y^{(i)}\log \left(h_{\theta }\left(x^{(i)}\right)\right)-\left(1-y^{(i)}\right)\log \left(1-h_{\theta }\left(x^{(i)}\right)\right)]$

def cost(theta, X, y):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
    second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
    return np.sum(first - second) / (len(X))

• 预处理 矩阵

#矩阵增加一列
data.insert(0, 'Ones', 1)

#X训练集 y目标变量
cols = data.shape[1]
X = data.iloc[:,0:cols-1]
y = data.iloc[:,cols-1:cols]

X = np.array(X.values)
y = np.array(y.values)
theta = np.zeros(3)

• 计算初始化参数的代价函数（theta == 0）

cost(theta, X, y)

• batch gradient descent(批量梯度下降)
  转换为向量化计算
  $$\frac{\partial J\left(\theta \right)}{\partial {\theta }_j}=\frac{1}{m}\sum _{i=1}^m(h_{\theta }\left(x^{(i)}\right)-y^{(i)})x_{{}_j}^{(i)}$$

计算梯度步长

​def gradient(theta, X, y):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    
    parameters = int(theta.ravel().shape[1])
    
    grad = np.zeros(parameters)
    
    error = sigmoid(X * theta.T) - y
    
    for i in range(parameters):
        term = np.multiply(error, X[:,i])
        grad[i] = np.sum(term) / len(X)
    return grad

使用Scipy实现寻找最优参数（TNC）

最优化函数fmin_tnc()

• 有约束的多元函数问题,提供梯度信息,使用截断牛顿法

---

1 调用

• scipy.optimize.fmin_tnc(func, x0, fprime=None, args=(),…)

---

2 最常使用的参数

• func:优化的目标函数
• x0:初值
• fprime:提供优化函数func的梯度函数,不然优化函数必须返回函数值和梯度,或者设置
• approx_grad:如果设置为True,会给出近似梯度
• args:元组,是传递给优化参数的参考

---

3 返回值

• x:数组,返回的优化问题目标值
• nfeval:整数,function evaluation的数目
• 在进行优化的时候,每当目标优化函数被调用一次,就算一个function evaluation.在一次迭代过程中会有>多次function evaluation.这个参数不等同于迭代次数,而往往大于迭代次数.

import scipy.optimize as opt
result = opt.fmin_tnc(func = cost, x0 = theta, fprime = gradient, args = (X, y))
result

• 代价函数的结果

cost(result[0], X, y)

• 使用所学的参数theta来为数据集X输出预测
  假设函数

$$h_{\theta }(x)=g\left({\theta }^{T}X\right)=P(y=1|x;\theta )$$$$g(x)=1/1+e^{-z}$$

当$h_{\theta }(x)$大于等于0.5时，预测y=1
当$h_{\theta }(x)$小于0.5时，预测y=0

def predict(theta, X):
    probability = sigmoid(X * theta.T)
    return [1 if x >= 0.5 else 0 for x in probability]

theta_min = np.matrix(result[0])
predictions = predict(theta_min, X)
correct = [1 if ((a == 1 and b ==1 ) or ( a== 0 and b == 0))else 0 for (a, b) in zip(predictions, y) ]
accuracy = (sum(map(int, correct)) % len(correct))
print('accuracy = {0}%'.format(accuracy))

• 训练集的准确性达到89%

3 预测芯片的好坏 正则化逻辑回归

• 数据可视化

path = 'ex2data2.txt'
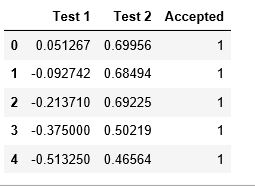
data2 = pd.read_csv(path, header = None, names = ['Test 1', 'Test 2', 'Accepted'])
data2.head()

positive = data2[data2['Accepted'].isin([1])]
negative = data2[data2['Accepted'].isin([0])]

fig,ax = plt.subplots(figsize=(8,6))
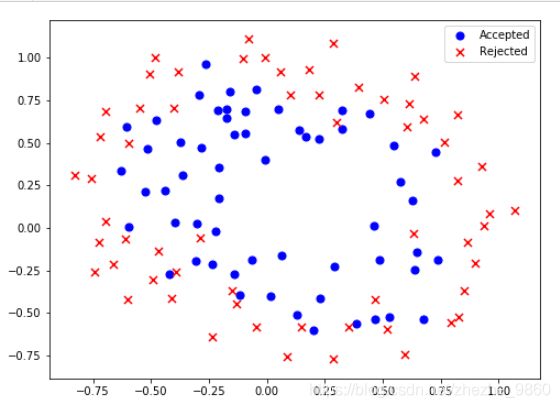
ax.scatter(positive['Test 1'], positive['Test 2'], s = 50, c = 'b', marker = 'o', label = 'Accepted')
ax.scatter(negative['Test 1'], negative['Test 2'], s = 50, c = 'r', marker = 'x', label = 'Rejected')

ax.legend()
ax.set_label('Test 1 Score')
ax.set_label('Test 2 Score')
plt.show()

数据没有线性决策界限来良好的分开两类数据
使用逻辑回归构造从原始的多项式中得到的特征

• 下面创建一组多项式特征：

degree = 5
x1 = data2['Test 1']
x2 = data2['Test 2']

data2.insert(3, 'ones', 1)

for i in range(1, degree):
    for j in range(0, i):
        data2['F' + str(i) + str(j)] = np.power(x1, i - j) * np.power(x2, j)
        
data2.drop('Test 1', axis = 1, inplace = True)
data2.drop('Test 2', axis = 1, inplace = True)

data2.head()

• 正则化代价函数(regularized cost)：
  $$J\left(\theta \right)=\frac{1}{m}\sum _{i=1}^m[-y^{(i)}\log \left(h_{\theta }\left(x^{(i)}\right)\right)-\left(1-y^{(i)}\right)\log \left(1-h_{\theta }\left(x^{(i)}\right)\right)]+\frac{\lambda }{2m}\sum _{j=1}^n{\theta }_j^2$$

def costReg(theta, X, y, learningRate):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
    second = np.multiply((1-y), np.log(1-sigmoid(X * theta.T)))
    reg = (learningRate / (2 * len(X))) * np.sum(np.power(theta[:,1:theta.shape[1]], 2))
    return np.sum(first - second) / len(X) + reg

• 梯度下降
  ${\theta }_j:={\theta }_j(1-a\frac{\lambda }{m})-a\frac{1}{m}\sum _{i=1}^m(h_{\theta }\left(x^{(i)}\right)-y^{(i)})x_j^{(i)}$

def gradientReg(theta, X, y, learningRate):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    
    parameters = int(theta.ravel().shape[1])
    grad = np.zeros(parameters)
    
    error = sigmoid(X * theta.T) - y
    
    for i in range(parameters):
        term = np.multiply(error, X[:,i])
        
        if(i == 0):
            grad[i] = np.sum(term)/len(X)
        else:
            grad[i] = (np.sum(term)/len(X)) + ((learningRate / len(X)) * theta[:,i])
    return grad

• 初始化变量

cols = data2.shape[1]
X2 = data2.iloc[:,1:cols]
y2 = data2.iloc[:,0:1]

X2 = np.array(X2.values)
y2 = np.array(y2.values)
theta2 = np.zeros(11)

• 学习率设置为1，调用正则化函数得到0.69，然后调用梯度下降函数
• 使用fmin_TNC优化函数计算

learningRate = 1
costReg(theta2, X2, y2, learningRate)
gradientReg(theta2, X2, y2, learningRate)
result2 = opt.fmin_tnc(func = costReg, x0 = theta2, fprime = gradientReg, args = (X2, y2, learningRate))
result2

使用第一部分的预测函数查看在训练数据的准确度

theta_min = np.matrix(result2[0])
predictions = predict(theta_min, X2)
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y2)]
accuracy = (sum(map(int, correct)) % len(correct))
print ('accuracy = {0}%'.format(accuracy))

准确率78%