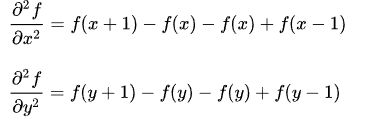Laplacian算子-Log算子-Dog算子边缘检测原理合集及实现

写在前面

这里，我们将Laplacian算子-Log算子-Dog算子合在一篇博文写，为什么呢？因为这3个算子有非常大的关联性：Dog算子可以近似Log算子，而Log(Laplacian of gaussain)算子的基础是Laplacian算子。所以合在一起写更加方便，也更加能够突出这种关联性和递进的关系。

值得说明的是：区别于Roberts算子、prewitt算子、sobel算子；Laplacian算子、Log算子、Dog算子均属于二阶微分算子。

Laplacian算子

拉普拉斯算子是最简单的各向同性微分算子，具有旋转不变性。一个二维图像函数的拉普拉斯变换是各向同性的二阶导数，定义为：

                                                                   

在图像中，将该方程表示为离散形式：

                         一维情况：

                                                    

                         二维情况：

                                    

上述是数学表达形式的拉普拉斯算子，那么我们可以将其表达为模板的形式：

                                                       

从卷积的形式来看，如果在图像中的一个比较暗的区域出现了一个亮点，那么经过拉普拉斯算子处理后，这个亮点怎么变得更亮，为什么会这样呢？

因为在一个很暗的区域内，很亮的点和其周围的点属于差异比较大的点，在图像上，反映到差异大，其实说的就是这个亮点与周围点的pixel在数值上的差距。那么基于二阶微分的拉普拉斯算子就是求取这种像素值发生突然变换的点或线，此算子却可用二次微分正峰和负峰之间的过零点来确定，对孤立点或端点更为敏感，因此特别适用于以突出图像中的孤立点、孤立线或线端点为目的的场合。同梯度算子一样，拉普拉斯算子也会增强图像中的噪声，有时用拉普拉斯算子进行边缘检测时，可将图像先进行平滑处理。但是在进行锐化的过程中，我们又不希望这个filter改变了图像中其他pixel的信息，所以保证了每个filter的数值和加起来为0（1+1+1+1-4）。

由于拉普拉斯是一种微分算子，它的应用可增强图像中灰度突变的区域，减弱灰度的缓慢变化区域。因此，锐化处理可选择拉普拉斯算子对原图像进行处理，产生描述灰度突变的图像，再将拉普拉斯图像与原始图像叠加而产生锐化图像。

拉普拉斯锐化的基本方法可以由下式表示：

                 

这种简单的锐化方法既可以产生拉普拉斯锐化处理的效果，同时又能保留背景信息，将原始图像叠加到拉普拉斯变换的处理结果中去，可以使图像中的各灰度值得到保留，使灰度突变处的对比度得到增强，最终结果是在保留图像背景的前提下，突现出图像中小的细节信息。

我们发现Laplacian算子进行边缘检测并没有像Sobel或Prewitt那样的平滑过程，所以它会对噪声产生较大的响应，并且无法分别得到水平方向、垂直方向或者其他固定方向的的边缘。但是它只有一个卷积核，所以计算成本会更低。

代码实现起来很简单，构造卷积核，与输入图像进行卷积即可。

Log(Laplacian of gaussain)算子

拉普拉斯边缘检测算子没有对图像做平滑处理，所以对噪声很敏感。因此可以想到先对图像进行高斯平滑处理，然后再与Laplacian算子进行卷积。这就是高斯拉普拉斯算子(Log)。

高斯函数：

                                                             (前面的常数省略了)

Log算子的表达式如下：

                               (前面的常数省略了)

为了更加直观地理解Log算子，下图分别为高斯函数、高斯函数一阶导、高斯函数二阶导的图像       ：
                                 

由于高斯函数（图1a）的二阶导数的3D图（图1c）倒置后，其形状有点像墨西哥草帽，因此，在业界也被称为墨西哥草帽小波（Mexican hat wavelet ）。  

从图像可以清楚地看出：可以通过检测滤波结果的零交叉（Zero crossings）获得图像或物体的边缘。

从具体实现的角度来讲，其实有两种实现方式，第一种是首先由Log算子的表达式构建卷积模板，然后对图像进行卷积，如下式：

                                                                  

常用的卷积模板是5*5的模板：

                                                                       

然而直接构造卷积模板的计算量较大，效率较低，所以一般采用第二种方式，因为卷积是线性操作，那么还可以写成如下：

                                                                 

上式指示了可以先用高斯平滑图像，最后再求其结果的拉普拉斯。

优缺点:

该算法的特点是由于先进行了高斯滤波，因而可以一定程度上克服噪声的影响。它的局限性在于以下两个方面：

（1）可能产生假边缘（false edges）；

（2）对一些曲线边缘（curved edges）的定位误差较大。

尽管该算法存在以上不足，但对未来图像特征研究起到了积极作用。尤其对图像先进行高斯滤波（噪声平滑）再进行图像梯度计算的思想的引入，被后来性能优良的Canny边缘检测算法(Canny edge detector )所采用。同时，这种思想也被后来很多的图像特征检测技术所采纳，如Harris角点，尺度不变特征变换（SIFT）等。

高斯差分(DOG)算子

Marr and Hildreth[1980]指出，使用高斯差分(DOG)来近似Log算子是可能的：

                                      

式中：。Marr and Hildreth建议，使用1.6：1的标准差比率能够对LOG函数提供一个更接近的“工程”近似。

再来看看DOG和LOG数学上的关系：

                 二维高斯函数对的偏导：

                                             

                 LOG：

                            

显然DOG和LOG有如下关系：

                                                                

 又根据一阶倒数的定义得到：                                                                                                                                                                        

根据上述两个公式，显然可以得到Log的近似：

                                                    

                                                  

                    即：

                                             

其中k−1是个常数，不影响边缘检测，LoG算子和DoG算子的函数波形对比如下图所示，由于高斯差分的计算更加简单，因此可用DoG算子近似替代LoG算子：

                                                             

具体实现：即用两个不同标准差的高斯核平滑图像，然后结果相减，最后阈值分割即可得到边缘检测结果。

 

DOG代码实现

#include 
#include 
#include 
#include 

///
//x，y方向联合实现获取高斯模板
//
void generateGaussMask(cv::Mat& Mask, cv::Size wsize, double sigma){
	Mask.create(wsize, CV_64F);
	int h = wsize.height;
	int w = wsize.width;
	int center_h = (h - 1) / 2;
	int center_w = (w - 1) / 2;
	double sum = 0.0;
	double x, y;
	for (int i = 0; i < h; ++i){
		y = pow(i - center_h, 2);
		for (int j = 0; j < w; ++j){
			x = pow(j - center_w, 2);
			//因为最后都要归一化的，常数部分可以不计算，也减少了运算量
			double g = exp(-(x + y) / (2 * sigma*sigma));
			Mask.at(i, j) = g;
			sum += g;
		}
	}
	Mask = Mask / sum;
}


//按二维高斯函数实现高斯滤波
///
void GaussianFilter(cv::Mat& src, cv::Mat& dst, cv::Mat window){
	int hh = (window.rows - 1) / 2;
	int hw = (window.cols - 1) / 2;
	dst = cv::Mat::zeros(src.size(), src.type());
	//边界填充
	cv::Mat Newsrc;
	cv::copyMakeBorder(src, Newsrc, hh, hh, hw, hw, cv::BORDER_REPLICATE);//边界复制

	//高斯滤波
	for (int i = hh; i < src.rows + hh; ++i){
		for (int j = hw; j < src.cols + hw; ++j){
			double sum[3] = { 0 };

			for (int r = -hh; r <= hh; ++r){
				for (int c = -hw; c <= hw; ++c){
					if (src.channels() == 1){
						sum[0] = sum[0] + Newsrc.at(i + r, j + c) * window.at(r + hh, c + hw);
					}
					else if (src.channels() == 3){
						cv::Vec3b rgb = Newsrc.at(i + r, j + c);
						sum[0] = sum[0] + rgb[0] * window.at(r + hh, c + hw);//B
						sum[1] = sum[1] + rgb[1] * window.at(r + hh, c + hw);//G
						sum[2] = sum[2] + rgb[2] * window.at(r + hh, c + hw);//R
					}
				}
			}

			for (int k = 0; k < src.channels(); ++k){
				if (sum[k] < 0)
					sum[k] = 0;
				else if (sum[k]>255)
					sum[k] = 255;
			}
			if (src.channels() == 1)
			{
				dst.at(i - hh, j - hw) = static_cast(sum[0]);
			}
			else if (src.channels() == 3)
			{
				cv::Vec3b rgb = { static_cast(sum[0]), static_cast(sum[1]), static_cast(sum[2]) };
				dst.at(i - hh, j - hw) = rgb;
			}

		}
	}

}


//DOG高斯差分
///
void DOG1(cv::Mat &src, cv::Mat &dst, cv::Size wsize, double sigma,double k=1.6){
	cv::Mat Mask1, Mask2, gaussian_dst1, gaussian_dst2;
	generateGaussMask(Mask1, wsize, k*sigma);//获取二维高斯滤波模板1
	generateGaussMask(Mask2, wsize, sigma);//获取二维高斯滤波模板2
	
	//高斯滤波
	GaussianFilter(src, gaussian_dst1, Mask1);
	GaussianFilter(src, gaussian_dst2, Mask2);

	dst = gaussian_dst1 - gaussian_dst2-1;

	cv::threshold(dst, dst, 0, 255, cv::THRESH_BINARY);
}



//DOG高斯差分--使用opencv的GaussianBlur

void DOG2(cv::Mat &src, cv::Mat &dst, cv::Size wsize, double sigma, double k = 1.6){
	cv::Mat gaussian_dst1, gaussian_dst2;
	//高斯滤波
	cv::GaussianBlur(src, gaussian_dst1, wsize, k*sigma);
	cv::GaussianBlur(src, gaussian_dst2, wsize, sigma);

	dst = gaussian_dst1 - gaussian_dst2;
	cv::threshold(dst, dst, 0, 255, cv::THRESH_BINARY);
}

int main(){
	cv::Mat src = cv::imread("I:\\Learning-and-Practice\\2019Change\\Image process algorithm\\Img\\Fig1025(a)(building_original).tif");
	if (src.empty()){
		return -1;
	}
	if (src.channels() > 1) cv::cvtColor(src, src, CV_RGB2GRAY);
	cv::Mat edge1,edge2;
	DOG1(src, edge1, cv::Size(7, 7), 2);
	DOG2(src, edge2, cv::Size(7, 7), 2);
	cv::namedWindow("src", CV_WINDOW_NORMAL);
	imshow("src", src);
	cv::namedWindow("My_DOG", CV_WINDOW_NORMAL);
	imshow("My_DOG", edge1);

	cv::namedWindow("Opencv_DOG", CV_WINDOW_NORMAL);
	imshow("Opencv_DOG", edge2);
	cv::waitKey(0);
	return 0;
}

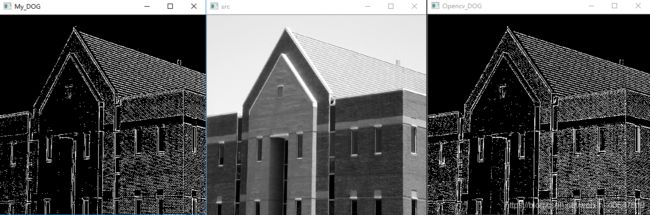
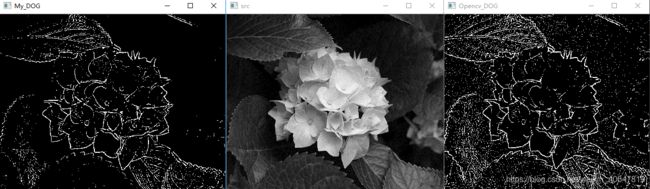
效果

 

 

参考：

《OpenCV算法精解》---张平

https://senitco.github.io/2017/06/20/image-feature-LoG-DoG/

 http://blog.sciencenet.cn/blog-425437-790731.html

https://zhuanlan.zhihu.com/p/49447503