C# FIR滤波器（含低通、高通、带通、带阻）

最近需要用到Fir滤波器，在网上也看了不少资料，发现一个稍微能用的（https://blog.csdn.net/BIGFatming/article/details/92386914），主要代码也是直接copy的，但是在使用过程中发现，三角窗的实现好像不对，而且只实现了低通的，根据该文章内容，我自己重写了一个，包括三角窗函数的实现，添加了高通、带通、带阻的实现。环境Visual Studio2015，c#。

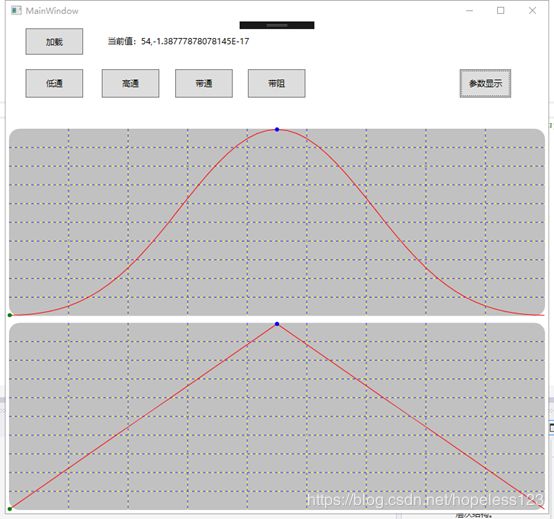
1、如下图（最下面的曲线），使用网友的三角函数实现不对；

2、据此更改了相关代码；

public class Bartlett
    {
        public int N = 0;
        public Bartlett(double Wp, double Ws)
        {
            int i;
            double n = (2.1 * 2 * Math.PI) / (Ws - Wp);
            for (i = 0; i < n; i++) ;
            N = i;
        }

        public double[] GetWin()
        {
            int n;
            double[] wd = new double[N];
            for (n = 0; n < N; n++)
            {
                if (n <= ((N - 1) / 2))
                {
                    wd[n] = (double)(2 * (double)n / ((double)N - 1));
                }
                if (n > ((N - 1) / 2))
                {
                    wd[n] = 2 * ((double)N - 1 - n) / ((double)N - 1);
                }
            }
            return wd;
        }
}

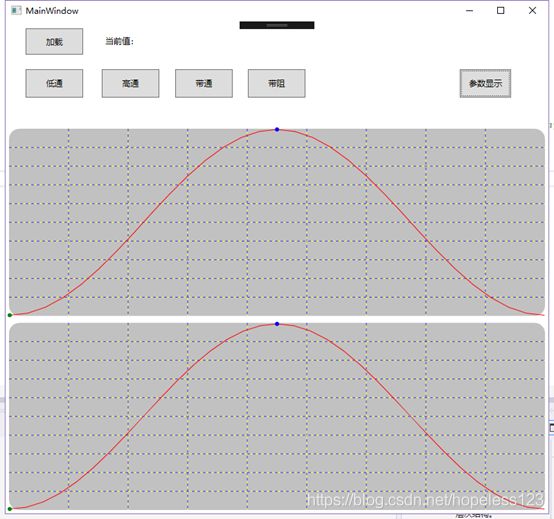
3、下图为Blackman和三角函数的h(n)；

4、下图为Hanning和Hamming窗的h(n)；

5、由于看到的资料只提供了低通的实现方式，根据《数字信号处理理论、算法与实现（第三版）》实现了对应的高通、带通、带阻的实现；

6、高通

public double[] GetHigh()
        {
            double[] hd = new double[N];
            for (int n = 0; n < N; n++)
            {
                double numerator = Math.Sin(Math.PI * (n - alpha)) - Math.Sin((n - alpha) * Wc);
                double denominator = Math.PI * (n - alpha);
                if (n == alpha)
                {
                    hd[n] = (Math.PI - Wc) / Math.PI;
                }
                else
                {
                    hd[n] = numerator / denominator;
                }
            }
            return hd;
        }

7、带通

public double[] GetDaiTong(double Wl, double Wh)
        {
            double[] hd = new double[N];
            for (int n = 0; n < N; n++)
            {
                double numerator = Math.Sin((n - alpha) * Wh) - Math.Sin((n - alpha) * Wl);
                double denominator = Math.PI * (n - alpha);
                if (n == alpha)
                {
                    hd[n] = (Wh - Wl) / Math.PI;
                }
                else
                {
                    hd[n] = numerator / denominator;
                }
            }
            return hd;
        }

8、带阻，这里设计时，对于求n=alpha时的hd[n]值不是很确定，上图中用红笔注释的地方（为下面代码实现的内容）。

注：能力有限，在分析原始算法时，我是无法求解n=alpha的值或表达式（有人知道原始算法如何求解的话请留言，3Q），故带阻的实现可能在n=alpha点时是错的。【后期再进行研究，及时更新】。

public double[] GetDaiZu(double Wl, double Wh)
        {
            double[] hd = new double[N];
            for (int n = 0; n < N; n++)
            {
                double numerator = Math.Sin((n - alpha) * Wl) + Math.Sin(Math.PI * (n - alpha)) - Math.Sin((n - alpha) * Wh);
                double denominator = Math.PI * ((double)n - alpha);
                if (n == alpha)
                {
                    hd[n] = (Math.PI - Wh) / Math.PI + Wl / Math.PI;
                }
                else
                {
                    hd[n] = numerator / denominator;
                }
            }
            return hd;
        }

9、测试：（测试代码均使用的hanning窗，测试低通、高通、带通与带阻功能）

9.1、原始信号参数为：Fs=1000，采样点数：2048，原始数据包含两个频率点数据5Hz和20Hz。Matlab代码：

f1=5;f2=20;f3=15;
t=0:0.001:2.049;
y=2*cos(2*pi*f1*t)+2*sin(2*pi*f2*t);
plot(t,y);
fid=fopen('test1.txt','wt');
fprintf(fid,'%d,',y);
fclose(fid);

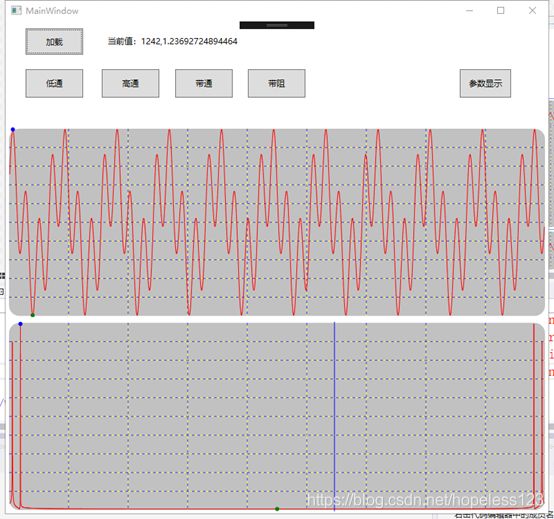
9.2、原始信号及频谱，

9.3、低通滤波，Wp=0.02 * Math.PI，Ws=0.03 * Math.PI（分别对应Wp=10Hz，Ws=15Hz）

注：由于给入的频率为归一化后的，需要计算（(Fs/2)*Wp=fp，截止频率为fc【Wc为归一化频率】）；相位延迟：(1/Fs)*(N-1)/2；滤波器阶数：N-1(N为窗长度)【这里不确定，网上查到有这个说法，有大神知道的话可以探讨一下】。

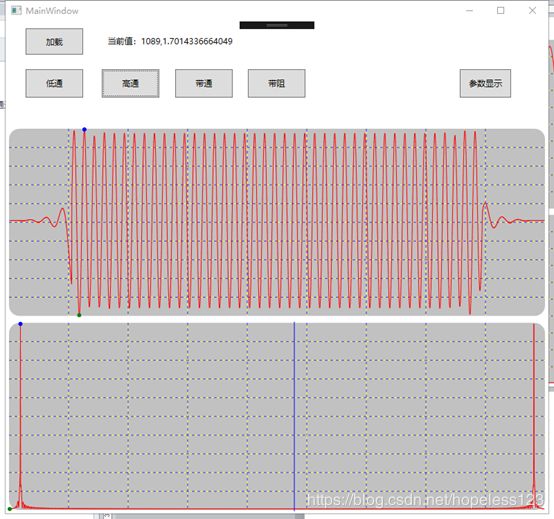
9.4、高通滤波，参数与低通一致，

9.5、带通滤波，带通频率设置为【0.03 * Math.PI, 0.05 * Math.PI】（即为15Hz~25Hz，通带）

9.6、带阻滤波，带通频率设置为【0.03 * Math.PI, 0.05 * Math.PI】（即为15Hz~25Hz，阻带）

10、总结：

1）基本能实现滤波功能，但是有很多参数以及算法需要再研究优化，仅提供一种思路；（未涉及到FIR的4种形式）

2）从效果来看，高通与带阻滤波后会出现很多高频的干扰（频段），而低通与带通没有，图中能看出，还需要进一步研究；

3）本文采用的是时域卷积的处理方式，其实也可以用差分方程来做，自己赖还没弄，处理完后都有数据点增多以及相移（线性）的问题，需要想办法优化；

4）整个测试代码https://download.csdn.net/download/hopeless123/12040952。

更新：5）在使用时发现，高通滤波时若信号含有直流分量，则滤波结束后可能会引入低频噪声，将直流分量滤除后再进行滤波效果就会好很多；