李航 统计学习方法 第一章 课后 习题 答案
最大似然估计参考文献:
https://guangchun.wordpress.com/2011/10/13/ml-bayes-map/
贝叶斯分布参考文献:
https://blog.csdn.net/a358463121/article/details/52562940
https://blog.csdn.net/guohecang/article/details/52313046
1、统计学习方法三要素:模型、策略、算法
2、伯努利模型
伯努利试验(Bernoulli experiment)是在同样的条件下重复地、相互独立地进行的一种随机试验,其特点是该随机试验只有两种可能结果:发生或者不发生。我们假设该项试验独立重复地进行了n次,那么就称这一系列重复独立的随机试验为n重伯努利试验,或称为伯努利概型。
定义随机变量A为一次伯努利试验的结果,A的取值为{0,1},概率分布为P(A):
P(A=1)=θ
P(A=0)=1−θ
3、最大似然估计
“似然”的意思就是“事情(即观察数据)发生的可能性”,最大似然估计就是要找到的θ一个估计值,使“事情发生的可能性”最大,也就是使p(D|θ)最大。一般来说,我们认为多次取样得到的x是独立同分布的,这样我们可以得到
p ( D ∣ θ ) = ∏ i = 1 n p ( x i ∣ θ ) p(D|\theta )=\prod _{i=1}^n p(x_{i}|\theta) p(D∣θ)=i=1∏np(xi∣θ)
那么我们求最大似然估计就是求 θ 的值,使得 p(D|θ) 最大。
即对于n次伯努利实验,有k次结果为1,则有:
p ( D ∣ θ ) = ∏ i = 1 n p ( x i ∣ θ ) = θ k θ n − k p(D|\theta )=\prod _{i=1}^n p(x_{i}|\theta)={θ^k}{θ^{n-k}} p(D∣θ)=i=1∏np(xi∣θ)=θkθn−k
得到最大值时候的θ值,即我们对公式对于θ求导可得:
p ( D ∣ θ ) = ∏ i = 1 n p ( x i ∣ θ ) = θ k θ n − k p(D|\theta )=\prod _{i=1}^n p(x_{i}|\theta)={θ^k}{θ^{n-k}} p(D∣θ)=i=1∏np(xi∣θ)=θkθn−k
d p ( D ∣ θ ) d θ = k θ k − 1 ( 1 − θ ) n − k − θ k ( 1 − θ ) n − k − 1 \frac{dp(D|\theta )}{dθ} =kθ^{k-1}{(1-θ)^{n-k}}-θ^{k}{(1-θ)^{n-k-1}} dθdp(D∣θ)=kθk−1(1−θ)n−k−θk(1−θ)n−k−1
则其倒数为零时,其最大似然估计得到最大值,即 θ = k n θ=\frac{k}{n} θ=nk
时其最大似然估计得到最大值。
-------------------------------------------------------
最大似然估计参考文献:
https://guangchun.wordpress.com/2011/10/13/ml-bayes-map/
4、贝叶斯估计
贝叶斯估计,是在给定训练数据D时,确定假设空间H中的最佳假设。即已知某个条件,预测一件事发生的概率是多大?
贝叶斯公式提供了从先验概率P(h)、P(D)和P(D|h)计算后验概率P(h|D)的方法。
公式:
p ( B ∣ A ) = P ( A ⋂ B ) P ( A ) = P ( A ∣ B ) P ( B ) P ( A ) p(B|A )=\frac{P(A\bigcap B)}{P(A)}=\frac{P(A| B)P(B)}{P(A)} p(B∣A)=P(A)P(A⋂B)=P(A)P(A∣B)P(B)
P(B|A) 为我们所求的后验概率。
P(A)是A的先验概率或边缘概率,称作"先验"是因为它不考虑B因素。
P(B|A)是已知A发生后B的条件概率,也称作B的后验概率,这里称作似然度。
P(B)是B的先验概率或边缘概率,这里称作标准化常量。
P(B|A)/P(B)称作标准似然度。
本题即为我们已知 分布D的条件下求 θ:
P ( θ ∣ A 1 , A 2 , . . . . , A n ) = P ( A 1 , A 2 , . . . . , A n ∣ θ ) p ( θ ) p ( A 1 , A 2 , . . . . , A n ∣ θ ) P(θ|A_{1},A_{2},....,A_{n})=\frac{P(A_{1},A_{2},....,A_{n}|θ){p(θ)}}{p(A_{1},A_{2},....,A_{n}|\theta)} P(θ∣A1,A2,....,An)=p(A1,A2,....,An∣θ)P(A1,A2,....,An∣θ)p(θ)
因为已知条件为伯努利模型。因此 P ( A 1 , A 2 , . . . . , A n ∣ θ ) P(A_{1},A_{2},....,A_{n}|θ) P(A1,A2,....,An∣θ)服从二项分布。即:
P ( A 1 , A 2 , . . . . , A n ∣ θ ) ∝ θ k θ n − k P(A_{1},A_{2},....,A_{n}|θ)\propto \theta^{k} \theta^{n-k} P(A1,A2,....,An∣θ)∝θkθn−k
p(θ)为先验分布,则 p(θ)可用Beta表示:
P ( ∣ θ ) ∝ θ a − 1 1 − θ b − 1 P(|θ) \propto {θ^{a-1}}{{1-θ}^{b-1}} P(∣θ)∝θa−11−θb−1
则: P ( θ ∣ A 1 , A 2 , . . . . , A n ) ∝ θ k θ n − k θ a − 1 1 − θ b − 1 P(θ|A_{1},A_{2},....,A_{n})\propto \theta^{k} \theta^{n-k}{θ^{a-1}}{{1-θ}^{b-1}} P(θ∣A1,A2,....,An)∝θkθn−kθa−11−θb−1
此时我们求得: θ = a r g a θ k θ n − k θ a − 1 1 − θ b − 1 θ = \underset{a}{arg}\theta^{k} \theta^{n-k}{θ^{a-1}}{{1-θ}^{b-1}} θ=aargθkθn−kθa−11−θb−1
对上式求导取零点得:
θ = k + ( a − 1 ) n + ( b − 1 ) + ( a − 1 ) θ =\frac{k + (a -1)}{n+(b -1)+(a - 1)} θ=n+(b−1)+(a−1)k+(a−1)
1.2
条件概率分布: P θ ( Y ∣ X ) P_{θ}(Y|X) Pθ(Y∣X)
对数损失函数: L ( Y , P ( Y ∣ X ) ) = − l o g P ( Y ∣ X ) L(Y, P(Y|X))=-logP(Y|X) L(Y,P(Y∣X))=−logP(Y∣X)
此时,经验风险R为:
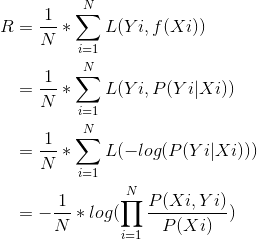
最小化经验风险,也就是最大化 P ( X i , Y i ) P(X_{i}, Y_{i}) P(Xi,Yi),这个就是极大似然估计。