OpenGL 入门12
原址:
http://ogldev.atspace.co.uk/www/tutorial13/tutorial13.html
http://blog.csdn.net/cordova/article/details/52650125
相机空间
我们已经学会了两种转换,一种转换用于改变物体的位置,旋转和缩放,我们可以使用这种类型的变换将物体放到3D世界中的任何一个位置。另一种变换是投影变换,他将三维空间中的点转换为二维平面中的点。转换后的二维坐标就能很容易映射到屏幕坐标了。
现在我们将要学习的这种转换将用来放置我们的摄像机的位置。在前面的教程中,我们都假设摄像机的位置位于三维世界的原点。在实际应用中,我们希望能够根据需要改变摄像机的位置,并把摄像机能够看到的物体投射到摄像机的projection window上。
下面的这张图显示了一个背对着我们的摄像机。在摄像机的前面,我们放置了一个虚拟的2D平面,用于模拟projection window所在的平面。任何在projection window之外的物体都会被裁切掉而不显示在屏幕上。

理论上来说,我们可以得到一个变换,用于将三维空间中的物体投影到这个二维平面上。不过,牵涉到的数学运算将会很复杂。当我们的摄像机位于原点,并且朝向在z轴方向时,这些投影变换计算是最简单的。比如我们的物体位于点(0,0,5),摄像机位于点(0,0,1)并且朝向这个物体。如果我们同时将物体和摄像机向z轴方向移动一个单位,那么此时摄像机就位于原点了,而这样做并不会改变我们的渲染结果,应为影响物体投影到该摄像机projection window上图像的四个参数(远平面位置,近平面位置,摄像机仰角,纵横比)并没有改变。同理,对场景中的所有物体随着摄像机想z轴方向移动1个单位,并不会改变屏幕上的显示结果。
这个示例里,我们的摄像机已经朝向z轴的方向,
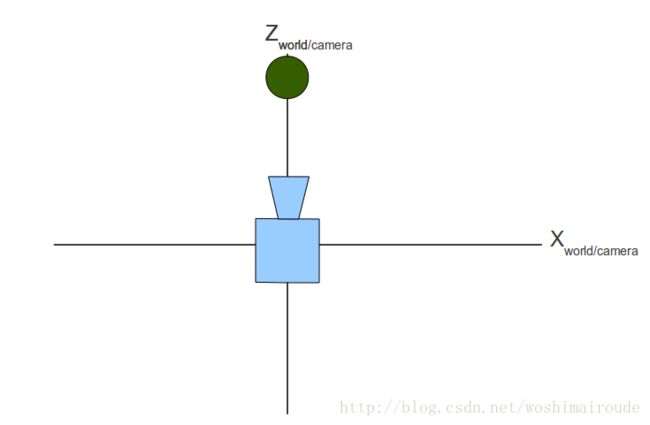
然而,当摄像机的朝向不是z轴的方向时,会发生啥呢?
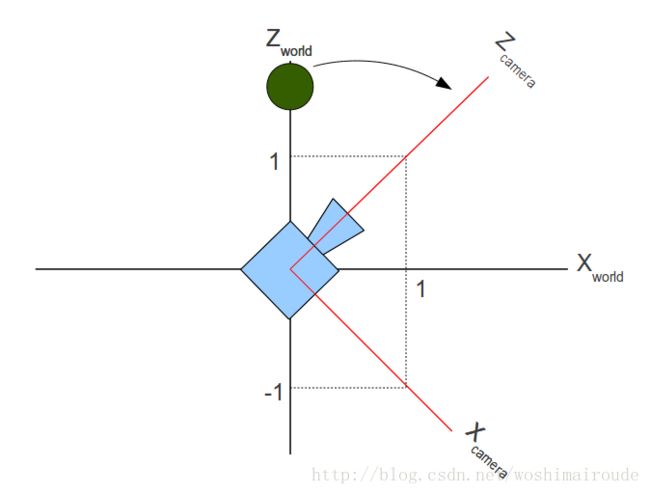
该摄像机最先是看着z轴的方向,不过他顺时针旋转了45度。从图中我们发现,摄像机也有自己的坐标系,并且这个坐标系可以与世界坐标系相同,也可以不相同。世界坐标系用于定义物体的位置,而摄像机坐标系用于定义摄像机的属性(摄像机哪边是前方,摄像机哪边是上方,摄像机哪边是右方)。这两个坐标系还有另一种称呼,前者为“世界空间”,后者为“相机空间”。
假设球的位置在世界空间是(0,y,z),然而在相机空间中,这个球的位置在这个相机空间的左上角,如何确定这个球在相机空间中的位置呢?如果我们知道这个球在相机空间中的位置,我们就可以用这个位置来计算投影变换,而不用去管什么世界空间坐标了(因为在相机空间中,相机的位置处于原点)。
我们之前说这个相机顺时针旋转了45度,换另一种说法就是我们的球逆时针旋转了45度。物体的运动是和相机的运动相反的。所以,我们需要在我们的变换序列中插入额外的变换,用于表明这种摄像机转动引起的球的位置的改变。这个变换将我们的摄像机移动到原点的同时,还要保证球离摄像机的相对位置不发生变化。如果把摄像机当作参照物的话,其实我们的物体就是在做与摄像机移动相反的移动。
移动摄像机的操作很简单,如果摄像机的坐标是(x,y,z),那么只需将摄像机移动(-x,-y,-z)就可以了。所以移动摄像机的矩阵就是:
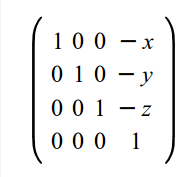
下一步就是将摄像机转到它所指向的世界空间的某个点的方向上去。我们需要知道空间中的某个点在摄像机空间中的位置。所以问题等价于如何将一个点的坐标转换到另一个坐标系中的坐标。
通过上图我们知道,一个世界坐标系其实是由三个方向的单位向量定义的:(1,0,0),(0,1,0),(0,0,1)。这三个向量中的任意两个向量构成的平面必定和第三个向量垂直。显而易见,第一我们的相机空间的三个坐标分别为:(1.0.-1),(0,1,0),(1,0,1)。将这些向量单位化之后得到的结果是:(0.7071,0,-0.7071), (0,1,0) 以及(0.7071,0,0.7071)。下图展示了这里的所述情况:
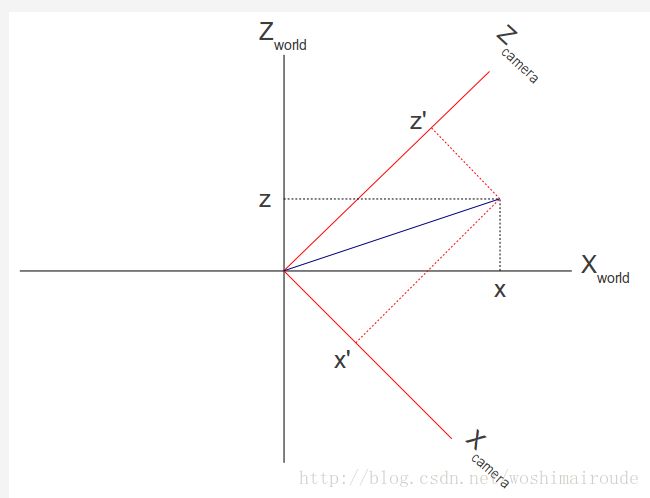
现在我们知道如何用世界坐标系中的单位向量来表示相机的坐标轴。现在我们要使用一种叫做“标量投影”的数学性质计算一个点在相机空间中的坐标。一个任意的向量A与一个单位向量B的点击得到的变量是向量A在B方向上的投影的长度。如果我们用世界空间中的点(x,y,z)乘以相机空间中代表x轴的方向的单位向量,我们就得到这个点在相机空间中对应的x坐标,y,z坐标也同理。
在OpenGL中定义相机空间的三个向量也叫做UVN系统。
N代表的是摄像机观察的点的坐标。在3D术语里面也叫做look-at vector
V代表的是如果我肩扛着摄像机时,我们头顶所朝向的方向
U代表的是如果我们肩扛摄像机时,表示右边的向量。
因此有如下的变换:

代码
struct {
Vector3f Pos;
Vector3f Target;
Vector3f Up;
} m_camera;
定义了一个m_camera的结构,用来存储定义相机空间所需的参数。
Vector3f Vector3f::Cross(const Vector3f& v) const
{
const float _x = y * v.z - z * v.y;
const float _y = z * v.x - x * v.z;
const float _z = x * v.y - y * v.x;
return Vector3f(_x, _y, _z);
}
用来计算叉积的函数,两个向量的叉积仍然为一个向量,且得到的向量和原来的两个向量构成的平面垂直。
Vector3f& Vector3f::Normalize()
{
const float Length = sqrtf(x * x + y * y + z * z);
x /= Length;
y /= Length;
z /= Length;
return *this;
}
讲一个向量单位化
void Matrix4f::InitCameraTransform(const Vector3f& Target, const Vector3f& Up)
{
Vector3f N = Target;
N.Normalize();
Vector3f U = Up;
U.Normalize();
U = U.Cross(Target);
Vector3f V = N.Cross(U);
m[0][0] = U.x; m[0][1] = U.y; m[0][2] = U.z; m[0][3] = 0.0f;
m[1][0] = V.x; m[1][1] = V.y; m[1][2] = V.z; m[1][3] = 0.0f;
m[2][0] = N.x; m[2][1] = N.y; m[2][2] = N.z; m[2][3] = 0.0f;
m[3][0] = 0.0f; m[3][1] = 0.0f; m[3][2] = 0.0f; m[3][3] = 1.0f;
}
根据输入的坐标确定相机空间的三个坐标。
const Matrix4f* Pipeline::GetTrans()
{
Matrix4f ScaleTrans, RotateTrans, TranslationTrans, CameraTranslationTrans, CameraRotateTrans, PersProjTrans;
ScaleTrans.InitScaleTransform(m_scale.x, m_scale.y, m_scale.z);
RotateTrans.InitRotateTransform(m_rotateInfo.x, m_rotateInfo.y, m_rotateInfo.z);
TranslationTrans.InitTranslationTransform(m_worldPos.x, m_worldPos.y, m_worldPos.z);
CameraTranslationTrans.InitTranslationTransform(-m_camera.Pos.x, -m_camera.Pos.y, -m_camera.Pos.z);
CameraRotateTrans.InitCameraTransform(m_camera.Target, m_camera.Up);
PersProjTrans.InitPersProjTransform(m_persProj.FOV, m_persProj.Width, m_persProj.Height, m_persProj.zNear, m_persProj.zFar);
m_transformation = PersProjTrans * CameraRotateTrans * CameraTranslationTrans * TranslationTrans * RotateTrans * ScaleTrans;
return &m_transformation;
}
这个函数用于获得完整的变换矩阵序列相乘所得的最终的变换矩阵。
Vector3f CameraPos(1.0f, 1.0f, -3.0f);
Vector3f CameraTarget(0.45f, 0.0f, 1.0f);
Vector3f CameraUp(0.0f, 1.0f, 0.0f);
p.SetCamera(CameraPos, CameraTarget, CameraUp);
设定相机空间的三个坐标轴的方向向量。